ref:http://blog.csdn.net/v_JULY_v/article/details/41209515
(详细推导见该链接)
LDA模型中用到的数学知识:
- 一个函数:gamma函数
- 四个分布:二项分布、多项分布、beta分布、Dirichlet分布
- 一个概念和一个理念:共轭先验和贝叶斯框架
- 两个模型:pLSA、LDA
- 一个采样:Gibbs采样
gamma函数和几个分布如下:
- gamma函数,阶乘在实数域上的推广
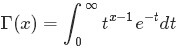
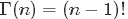
- 二项分布(Binomial distribution)
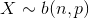 。简言之,只做一次实验,是伯努利分布,重复做了n次,是二项分布。二项分布的概率密度函数为:
。简言之,只做一次实验,是伯努利分布,重复做了n次,是二项分布。二项分布的概率密度函数为:
对于k = 0, 1, 2, ..., n,其中的
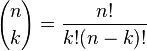 是二项式系数(这就是二项分布的名称的由来),又记为
是二项式系数(这就是二项分布的名称的由来),又记为
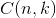 。回想起高中所学的那丁点概率知识了么:想必你当年一定死记过这个二项式系数
。回想起高中所学的那丁点概率知识了么:想必你当年一定死记过这个二项式系数
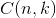 就是
就是
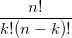 。
。
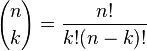 是二项式系数(这就是二项分布的名称的由来),又记为
是二项式系数(这就是二项分布的名称的由来),又记为
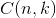 。回想起高中所学的那丁点概率知识了么:想必你当年一定死记过这个二项式系数
。回想起高中所学的那丁点概率知识了么:想必你当年一定死记过这个二项式系数
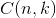 就是
就是
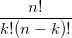 。
。
- 多项分布,是二项分布扩展到多维的情况
多项分布是指单次试验中的随机变量的取值不再是0-1的,而是有多种离散值可能(1,2,3...,k)。比如投掷6个面的骰子实验,N次实验结果服从K=6的多项分布。其中
![]()
多项分布的概率密度函数为:
- Beta分布,二项分布的共轭先验分布
给定参数

![]() 和
和
![]()
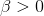 ,取值范围为[0,1]的随机变量 x 的概率密度函数
,取值范围为[0,1]的随机变量 x 的概率密度函数
![]() :
:

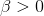 ,取值范围为[0,1]的随机变量 x 的概率密度函数
,取值范围为[0,1]的随机变量 x 的概率密度函数
其中
![]() :
:
,
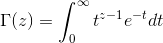
。
注:
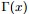 便是所谓的gamma函数,下文会具体阐述。
便是所谓的gamma函数,下文会具体阐述。
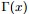 便是所谓的gamma函数,下文会具体阐述。
便是所谓的gamma函数,下文会具体阐述。
- Dirichlet分布,是beta分布在高维度上的推广
Dirichlet分布的的密度函数形式跟beta分布的密度函数如出一辙:
![]()
其中
至此,我们可以看到
二项分布和多项分布很相似,
Beta分布和Dirichlet 分布很相似,而至于
“Beta分布是二项式分布的共轭先验概率分布,而狄利克雷分布
(Dirichlet分布)是多项式分布的共轭先验概率分布










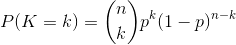
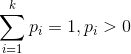
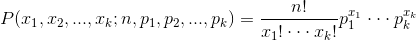

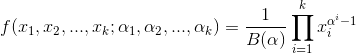
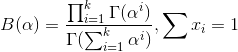
















 3369
3369

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








