伽马函数（Gamma函数）全面解析（包含课外扩展知识）与其在考研数学应用中的分析（具体举出了例题并附上解析）

一、伽马函数的定义与基本公式

1. 定义式

伽马函数是阶乘在复数域的推广，其标准定义为：

通过变量替换 x=，可变形为：

​

2. 核心性质

• 递推关系：
  
• 余元公式：
  
• 特殊值：
  

---

二、关键公式推导

1. 递推关系推导

由分部积分法：

​

2. Γ(1/2)的推导

使用极坐标法计算：

也就是高斯积分结果，具体如下：

---

三、衍生公式与关联函数

1. 贝塔函数（Beta函数）

定义式：

2. 斯特林公式（近似计算）

阶乘的渐近估计，当 nn 较大时：

---

四、常见题型分类

1. 积分计算

例题1：

解析：直接应用伽马函数定义：

 

例题2：

解析：转化为伽马函数形式：

2. 概率分布（伽马分布）

概率密度函数：

五、考研真题及解析

真题示例

题目（改编自历年真题）计算积分：

解析：

1. 变量替换 y=2x，则 dx=dy/2
2. 原式转化为：

​

六、高难度例题解析

例题：证明题：

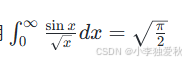
解析：

1. 利用复数积分与伽马函数关系：
2. 取虚部得：
   

---

七、易错点与解题技巧

易错点

1. 变量替换错误：例如在计算时，未将 k的幂次调整正确。
2. 混淆阶乘与伽马函数：将 Γ(n)误认为 n!（实际为 (n−1)!）
3. 忽略收敛条件：例如在应用余元公式时未考虑 α∉Z 的限制。

解题技巧

1. 标准化积分形式：将积分转化为 
   
2. 利用对称性：例如通过极坐标法计算二维积分简化问题。
3. 结合贝塔函数：

---

结语

伽马函数作为连接离散与连续数学的核心工具，在考研数学中具有重要应用，尤其在反常积分计算（如含参量积分、无穷积分）和概率分布推导（如伽马分布、卡方分布）中作用显著。其核心价值体现在三个方面：

        一是递推关系Γ(x+1) = xΓ(x)的灵活运用，可将复杂积分化简为已知形式；

        二是关键特殊值的记忆（如Γ(1/2)=√π），能直接用于计算含指数函数与幂函数的积分；

        三是与贝塔函数的联系（B(a,b)=Γ(a)Γ(b)/Γ(a+b)），为处理联合概率密度等问题提供高效解法。

考生需通过大量练习掌握变量替换技巧（如极坐标代换处理Γ(1/2)积分），并结合递推公式与特殊值快速破解复杂题目，同时注意伽马函数与概率分布的关联性（如卡方分布是Γ函数的特例），以提升解题速度和准确率。

---