最小生成树--Prim算法和Kruskal算法

概述

Prim算法和Kruskal算法，是用来求加权连通图的最小生成树的算法。

意即由此算法搜索到的边子集所构成的树中，不但包括了连通图里的所有顶点，且其所有边的权值之和亦为最小。

—————————————————————————————————————————————————————————————————————————————

Prim算法

基本思想

从单一顶点开始，普里姆算法按照以下步骤逐步扩大树中所含顶点的数目，直到遍及连通图的所有顶点。

1. 输入：一个加权连通图，其中顶点集合为V，边集合为E；

2. 初始化：V_new = {x}，其中x为集合V中的任一节点（起始点），E_new = {}；

3. 重复下列操作，直到V_new = V：

   1. 在集合E中选取权值最小的边（u, v），其中u为集合V_new中的元素，而v则是V中没有加入V_new的顶点（如果存在有多条满足前述条件即具有相同权值的边，则可任意选取其中之一）；

   2. 将v加入集合V_new中，将（u, v）加入集合E_new中；

4. 输出：使用集合V_new和E_new来描述所得到的最小生成树。

示例：

	说明	不可选	可选	已选
	此为原始的加权连通图。每条边一侧的数字代表其权值。	-	-	-
	顶点D被任意选为起始点。顶点A、B、E和F通过单条边与D相连。A是距离D最近的顶点，因此将A及对应边AD以高亮表示。	C, G	A, B, E, F	D
	下一个顶点为距离D或A最近的顶点。B距D为9，距A为7，E为15，F为6。因此，F距D或A最近，因此将顶点F与相应边DF以高亮表示。	C, G	B, E, F	A, D
	算法继续重复上面的步骤。距离A为7的顶点B被高亮表示。	C	B, E, G	A, D, F
	在当前情况下，可以在C、E与G间进行选择。C距B为8，E距B为7，G距F为11。E最近，因此将顶点E与相应边BE高亮表示。	无	C, E, G	A, D, F, B
	这里，可供选择的顶点只有C和G。C距E为5，G距E为9，故选取C，并与边EC一同高亮表示。	无	C, G	A, D, F, B, E
	顶点G是唯一剩下的顶点，它距F为11，距E为9，E最近，故高亮表示G及相应边EG。	无	G	A, D, F, B, E, C
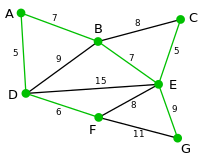	现在，所有顶点均已被选取，图中绿色部分即为连通图的最小生成树。在此例中，最小生成树的权值之和为39。	无	无	A, D, F, B, E, C, G

算法实现：

#include<iostream>
using namespace std;

const int INF = 999999;
const int MAXV = 10000;
int vnum, edgenum, start;

// 邻接矩阵 
int edge[MAXV][MAXV];
// 记录Vnew中每个点到V中邻接点的最短边
int lowcost[MAXV];
// 标记某点是否加入Vnew
int addVnew[MAXV];
// 记录V中与Vnew最邻近的点
int adj[MAXV];

void prim(int start)
{
	// 最小生成树的权值 
	int sumweight = 0;
	int i, j;
	int k = 0;
	for(i=1;i<=vnum;++i)
	{
		lowcost[i] = INF;
		adj[i] = start;		
	}
	// 顶点从1开始 
	for(i=1;i<=vnum;++i)
	{
		// 将所有点至于Vnew之外,V之内
		// 这里只要addVnew对应的值为-1，就表示在Vnew之外
		lowcost[i] = edge[start][i];
		addVnew[i] = -1;
	}
	// 将起始点start加入Vnew
	addVnew[start] = 0;
	adj[start] = start;
	for(i=1;i<=vnum;++i)
	{
		// 由于从start开始的，因此不需要再对第start个顶点进行处理
		if(start==i)
			continue;
		int min = INF;
		int v = -1;
		for(j=1;j<=vnum;++j)
		{
			// 在Vnew之外寻找最短路径
			if(addVnew[j]==-1 && lowcost[j]<min)
			{
				min = lowcost[j];
				v = j;
			}
		}
		if(v!=-1)
		{
			// 输出新加入的边 
			cout<<adj[v]<<" "<<v<<" "<<lowcost[v]<<endl;
			// 将v加Vnew中
			addVnew[v] = 0;
			// 计算路径长度之和
			sumweight += lowcost[v];
			for(j=1;j<=vnum;++j)
			{
				if(addVnew[j]==-1 && edge[v][j]<lowcost[j])
				{
					// 此时v点加入Vnew 需要更新lowcost
					lowcost[j] = edge[v][j];
					adj[j] = v;
				}
			}
		}
	}
	// 输出最小生成树的权值 
	cout<<sumweight<<endl;
}

int main()
{
	while(cin>>vnum>>edgenum>>start)
	{
		for(int i=1;i<=vnum;++i)
		{
			for(int j=1;j<=vnum;++j)
			{
				if(i==j)
					edge[i][j] = 0;
				else
					edge[i][j] = INF;
			}
		}
		int p, q, val;
		for(int i=1;i<=edgenum;++i)
		{
			cin>>p>>q>>val;
			edge[p][q] = val;
			edge[q][p] = val;
		}
		prim(start);
	}
	return 0;
}

测试案例：

输入

7 11 4
1 2 7
1 4 5
2 3 8
2 4 9
2 5 7
3 5 5
4 5 15
4 6 6
5 6 8
5 7 9
6 7 11

输出

4 1 5
4 6 6
1 2 7
2 5 7
5 3 5
5 7 9
39

————————————————————————————————————————————————————————————————————————————

Kruskal算法

基本思想：

按照权值从小到大选择n-1条边，且保证这n-1条边不形成回路。

首先构造一个只含有n个顶点的森林，然后依照权值从小到大从联通网中选择边加入到深林中，并使森林不产生回路，直至森林变成一棵树为止。

示例：

要点：

1）对图的所有边按照权值从小到大进行排序

解决方法：采用排序算法进行排序

2）将边添加到最小生成树中时，判断是否形成了回路

解决方法：记录顶点在最小生成树中的终点，然后每次需要将一条边添加到最小生成树时，判断该边的两个顶点的终点是否重合，重合的话会构成回路。

伪代码：

Kruskal()
{
    对边的权值从小到大进行排序;
    初始化每个顶点的终点为它自己;
    对于所有的边（u,v）：
        找到顶点u的终点x;
        找到顶点v的终点y;
        如果（x!=y）：
            将边(u,v)加入到最小生成树中;
            修改顶点u的终点;
}

算法实现：

#include<iostream>
#include<algorithm>
using namespace std;
// 最大边的数量 
const int MAXE = 20000;
// 最大顶点的数量
const int MAXV = 20000; 
// 边的结构体 
struct edge
{
	int u, v, cost;
};

// 数组，用来保存所有的边 
edge road[MAXE];
// 数组，用来保存对应顶点的终点 
int endpoint[MAXV];

// sort需要的比较函数 
bool cmp(const edge &e1, const edge &e2)
{  
    return e1.cost<e2.cost;  
}

// find函数返回顶点x的终点 
int find(int x)
{  
    if (endpoint[x] == x) return x;  
    else return endpoint[x] = find(endpoint[x]);  
}  

// unite函数的结果是将顶点x和顶点y加入到最小生成树中 
void unite(int x, int y)
{  
    x = find(x);  
    y = find(y);  
    // 终点一样则不发生变化 
    if (x == y) return;  
    // 否则，修改x的终点为y 
    else endpoint[x] = y;  
}  

// init函数的结果是将所有顶点的终点初始化为自己 
void init(int vexnum)
{
	for(int i=0;i<vexnum;++i)
		endpoint[i] = i;
}

int KRUSKAL(int vexnum, int edgenum)
{
	// ans用于记录最小生成树的总权值 
	int ans = 0;
	// 初始化每个顶点的终点为它自己
	init(vexnum);
	//  对边的权值从小到大进行排序
	sort(road, road+edgenum, cmp);
	for(int i=0;i<edgenum;i++){  
        if(find(road[i].u)!=find(road[i].v)){  
        	// 将边(u,v)加入到最小生成树中
            // 修改顶点u的终点;
            unite(road[i].u, road[i].v);  
            ans += road[i].cost;  
        }  
    }
	return ans;
}

int main()
{
	int vexnum, edgenum;
	cin>>vexnum>>edgenum;
	for(int i=0;i<edgenum;++i)
	{
		cin>>road[i].u>>road[i].v>>road[i].cost;
	}
	cout<<KRUSKAL(vexnum, edgenum)<<endl;
	return 0;
}

测试案例：

输入

7 11
0 1 7
0 3 5
1 2 8
1 3 9
1 4 7
2 4 5
3 4 15
3 5 6
4 5 8
4 6 9
5 6 11

输出

39

参考资料：

维基百科、如果天空不死--博客园、华山大师兄--博客园