Prefix Sums CodeForces - 837F（思维+二分+组合数）

Prefix Sums

CodeForces - 837F

Consider the function p(x), where x is an array of m integers, which returns an array y consisting of m + 1 integers such that y_i is equal to the sum of first i elements of array x (0 ≤ i ≤ m).

You have an infinite sequence of arrays A⁰, A¹, A²..., where A⁰ is given in the input, and for each i ≥ 1 Aⁱ = p(A^i - 1). Also you have a positive integer k. You have to find minimum possible i such that Aⁱ contains a number which is larger or equal than k.

Input

The first line contains two integers n and k (2 ≤ n ≤ 200000, 1 ≤ k ≤ 10¹⁸). n is the size of array A⁰.

The second line contains n integers A⁰₀, A⁰₁... A⁰_n - 1 — the elements of A⁰ (0 ≤ A⁰_i ≤ 10⁹). At least two elements of A⁰ are positive.

Output

Print the minimum i such that Aⁱ contains a number which is larger or equal than k.

Examples

Input

2 2
1 1

Output

1

Input

3 6
1 1 1

Output

2

Input

3 1
1 0 1

Output

0

题意:

p(x)表示对于一个元素个数为m的x的序列,会产生一个序列y 为m+1个元素,且有y[i]=sum(x[j]) 0<=j<i

现在给你一个长度为n的序列A0,给你一个k,问你要至少进行几次操作,使得Ai 当中存在某一个元素的值>=k。

     Ai = p(Ai-1)

每次对于第一个数组元素来说，它的前面没有，因此每次新生成的数组第一个元素都将为0，我们可以忽略掉，所以每次数组都是n个元素，其次明确 A0的每个元素都是>=0的,那么也就是说新产生的序列中最后一个元素一定是所有数中最大的.那么如果最后一个满足就一定可以了.那么我们来看看能不能快速的求出新产生的序列的最后一个值.然后观察规律

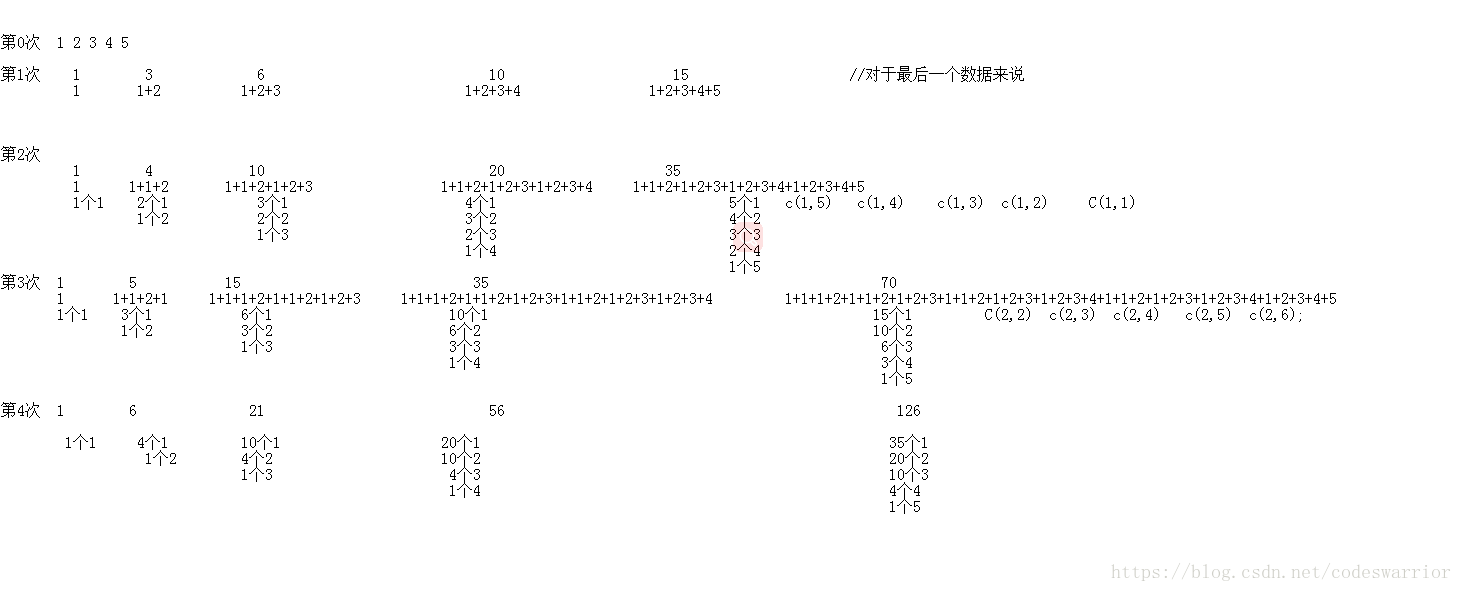
我们观察k = 2的这一行，对于最后一个元素我们发现a[0]有5个即C(1,5),a[1]有4个即C(1,4),a[2]有3个C(1,3),a[3]有2个C(1,2)
a[4]有1个C(1,1).所以对于k=2时，最后一个元素的大小就是 a[0]*C(1,5) + a[1]*C(1,4) + ……+a[4]*C(1,1)，之后亦是如此
那么我们就需要求这些组合数，他们存在一些特点，C上面的数始终是k-1，而下面的数虽然变化也是有规律的，发现从i=0到i=4遍历下面的数字就是上面的k-1每次加上n-1-i，这样C的上下元素都有了就可以求组合数了。然后需要二分答案

code：

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
typedef long long ll;
const int maxn = 2e5 + 10;
ll n,k;
ll a[maxn];
bool check(ll x){
    double sum = 0,tmp = 0;//sum计算最后一个数据的值，tmp计算原数组a中的每个值对sum的贡献值大小
    for(int i = 0; i < n; i++){
       if(a[i] == 0)
         continue;
       ll y = n - 1 - i;
       ll mm = x - 1,nn = mm + y;//mm是C上面的数字观察可知总是比k小1，nn是下面的数字a数组有n-1个数字，nn就有
                                 //n-1种数字，并且a数组中下标越小，nn越大
       mm = min(nn - mm,mm);
       tmp = a[i];
       for(ll j = 1; j <= mm; j++){//算组合数
          tmp = tmp * (nn - mm + j) / j;
          if(tmp >= k)
            return true;
       }
       sum += tmp;
       if(sum >= k)
        return true;
    }
    return false;
}
void solve(){//二分答案
    ll l = 1,r = k,mid;//因为至少有一个1，所以最多k次完成
    while(l <= r){
        mid = (l + r) >> 1;
        if(check(mid)){
            r = mid - 1;
        }
        else{
            l = mid + 1;
        }
    }
    printf("%lld\n",l);
    return;
}
int main(){
    scanf("%lld%lld",&n,&k);
    int flag = 0;
    for(int i = 0; i < n; i++){
        scanf("%lld",&a[i]);
        if(a[i] >= k)
            flag = 1;
    }
    if(flag)
        puts("0");
    else
        solve();
    return 0;
}