一、矩阵对角化的理论
一个映射或者一个线性变换,都有一个矩阵和它相对应。矩阵或者映射是不是可以对角化,对工程应用来说比较重要,因为对角化后的矩阵,乘积简单,经过多次变换的话,相当于矩阵的多次方。矩阵能不能对角化,取决于它的特称向量能否构成矩阵的一个基。
1.在域 F 上的 n × n 矩阵 A 是可对角化的,当且仅当它的特征空间的维度等于 n,它为真当且仅当存在由 A 的特征向量组成的Fn的基。如果找到了这样的基,可以形成有基向量作为纵列的矩阵 P,而 P-1AP 将是对角矩阵。这个矩阵的对角元素是 A 的特征值。
2. 线性映射 T : V → V 是可对角化的,当且仅当它的特征空间的维度等于 dim(V),它为真当且仅当存在由 T 的特征向量组成的 V 的基。T 关于这个基将表示为对角矩阵。这个矩阵的对角元素是 T 的特征值。
另一个特征化: 矩阵或线性映射在域 F 上可对角化的,当且仅当它的极小多项式在 F 上有不同的线性因子。
下列充分(但非必要)条件经常是有用的。
1. n × n 矩阵 A 只在域 F 上可对角化的,如果它在 F 中有 n 个不同的特征值,就是说,如果它的特征多项式在 F 中有 n 个不同的根。
2. 线性映射 T : V → V 带有 n=dim(V) 是可对角化的,如果它有 n 个不同的特征值,就是说它的特征多项式在 F 中有 n 个不同的根。
3. 在域 F 上的 n × n 矩阵 A,如果重根的维数等于其线性无关的特征向量的个数,则矩阵A可以对角化。
4.
二、矩阵对角化过程
下面例子中,矩阵A是对称的,它可以进行对角化,虽然它只有2个不同的特征值,但是有4个线性无关的特征向量,所以能进行对角化。
给定矩阵A,求它的特征值、特征向量,并对它进行对角化。
(1)求特征多项式,matlab命令p= poly(A);
(2)求解特征多项式,求出特征值,solve(P);
(3)分别将特征值带入齐次方程组,求出基础解系
(4)针对每个特征值下的基础解系,进行正交化。
(5)对正交化后的向量单位化
例子:已知
求出一正交矩阵 使 成对角形.
解:先求出的 特征值.由
即得的特征值为 &#









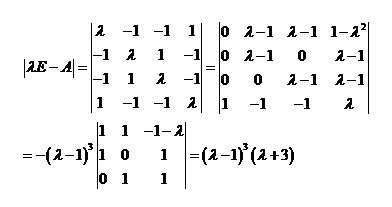
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








