最小二乘法是一种数学统计方法,从拟合的角度理解,它可以使拟合的误差(即实际值与拟合值之差)的平方和达到最小。这种方法在回归分析、曲线拟合、求解超定方程组等领域有广泛应用。
线性最小二乘问题的数学形式
对于线性回归问题,我们通常有一个形式为的模型,其中:
y 是观测到的因变量(响应)向量。
X是设计矩阵,包含观测到的自变量(解释变量)的值。是要估计的参数向量。
是误差向量。
最小二乘估计的目标是找到使残差平方和最小的 值,即:
这可以通过求解正规方程来得到,从而得到最小二乘估计
。
最简单的MATLAB代码如下:
clc;close all;clear all;warning off;%清除变量
rand('seed', 100);
randn('seed', 100);
format long g;
% 生成模拟数据
x = (0:0.1:10)'; % 自变量
beta = [2; -1]; % 真实参数值
y = [ones(size(x,1),1),x] * beta + randn(size(x,1),1) * 0.5; % 因变量,加入一些噪声
% 使用最小二乘法进行拟合
X = [ones(size(x)), x]; % 设计矩阵,包括截距项和x项
beta_hat = (X' * X) \ (X' * y); % 求解正规方程得到参数估计值
% 绘制实际值和拟合值图像
figure;
plot(x, y, 'ro', 'MarkerFaceColor', 'r'); % 绘制实际值点图,红色圆圈表示
hold on;
y_fit = X * beta_hat; % 计算拟合值
plot(x, y_fit, 'b-'); % 绘制拟合线,蓝色实线表示
xlabel('x');
ylabel('y');
legend('实际值', '拟合值');
title('最小二乘拟合');
grid on;
hold off;程序结果如下:
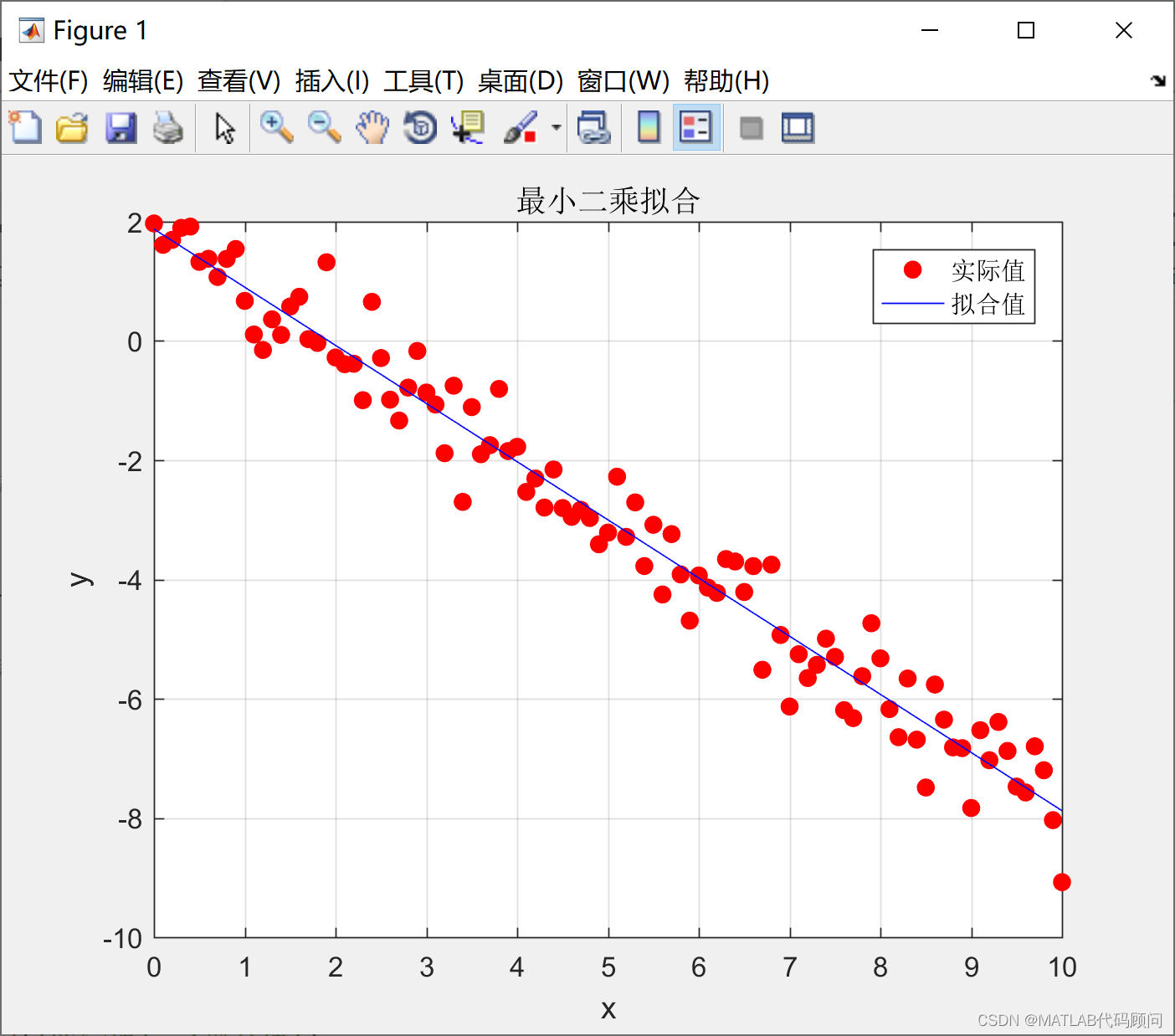








 本文介绍了最小二乘法作为一种数学统计方法,尤其在线性回归中的应用,通过实例展示了如何使用MATLAB编程求解线性最小二乘问题并生成拟合曲线。
本文介绍了最小二乘法作为一种数学统计方法,尤其在线性回归中的应用,通过实例展示了如何使用MATLAB编程求解线性最小二乘问题并生成拟合曲线。


















 2521
2521

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










