线性回归与梯度下降

一、梯度下降（Gradient descent）

在讲解梯度下降之前，先要了解什么是偏导数和梯度。

1.偏导数（partial derivative）

  在二维坐标系中，求一个点的切线斜率，其实就是求这个点的导数；在多维坐标系中，影响函数变化的变量可能不止一个，因此画出的图像也是立体的，对于图像中的一个点，它的导数可能有多个，因为在每个变量的方向上均可以求导。我们将点$x$ 处只有变量$x_i$ 增加时$f(x)$ 的变化就叫做求偏导数。记作 $\frac{\partial }{\partial x_i}f(\mathbf{x})$.

---

2.梯度（gradient）

  梯度就是相对于一个向量求导的导数，其结果仍然为一个向量。
直白的讲，梯度就是多维图像中一个点对所有变量分别做偏导的后集合。
例如二维向量的偏导：
$$\nabla L(\theta )=\left[\begin{array}{l}\partial L\left({\theta }_1\right)/\partial {\theta }_1\\ \partial L\left({\theta }_2\right)/\partial {\theta }_2\end{array}\right]$$
梯度有一个很重要的特点，就是函数中的一个点沿梯度方向变化最快。
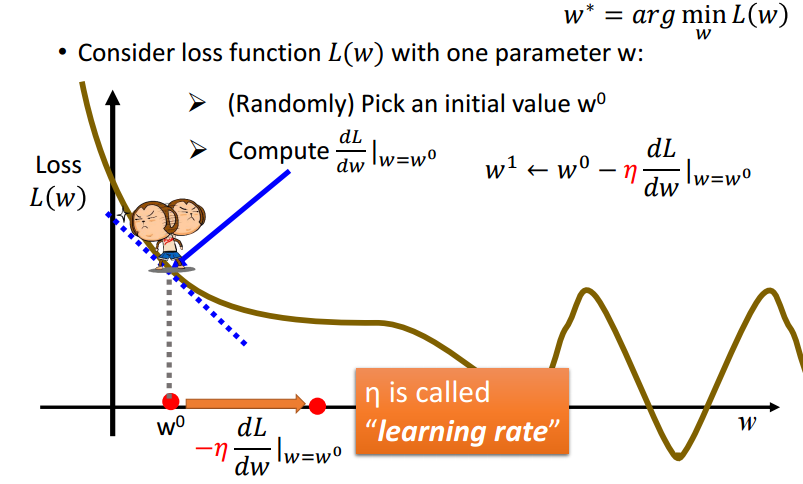
  如果把函数的图像看作是群山，一个人想要以最快速度下山，那么只需让这个人每次沿梯度方向下降一段距离，迭代进行此步骤即可。如下图的猴子。

  将上面提到的“一段距离”记作$\eta \frac{dL}{dw}$，其中$\eta$ 叫做学习率（Learning rate），可以将其视作走了多少步，将后面的偏导视为下山的步长。
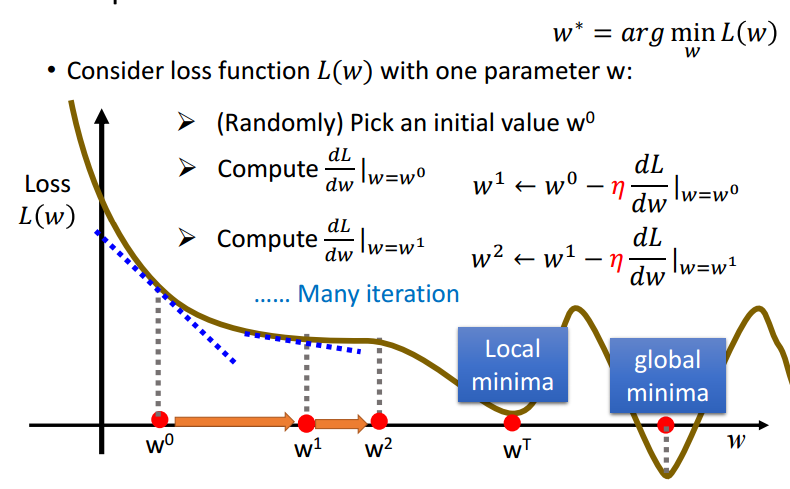
  梯度下降可能遇到的问题——遇到鞍点或者陷入局部最小值：

---

二、线性回归（Linear regression）

1. 线性回归

线性回归就是利用回归分析来确定两种或两种以上变量间相互关系的方法，输入为向量，输出为标量，一般形式为：
$$y=w\ast x+b$$
其中$w$ 代表权重 $Weight$，$b$ 则代表偏移量$Bias$.

举个线性回归例子：

  上面的模型中，输入可能为股票状态，则经过一个线性系统后，输出为道琼斯指数；输入为当前路况，输出为方向盘角度；输入为商品信息，输入为商品被购买的可能性…这些都是线性回归。

---

2. 最小二乘法

  假如现在已知了一组完整的数据$S_1$（包括输入值$x$ 与输出值$y$ ，如上图），我们手里有另外一组只包括输入值$x$的数据$S_2$，想要预测$S_2$的输出结果为多少，应该怎么做呢？
  一个直观的方法是，将已知的数据用一条光滑的曲线（直线）连接在一起构成（拟合）一个模型，遇到后续的测试数据时，只需要将测试数据作为输入放到模型中，即可输出预测的结果。
  当然，模型的选择（即模型的参数$w$ 与 $b$）不能是随意的，一个好的线性回归模型应该满足使训练集的数据$y$ 尽可能靠近拟合出来的曲线，也就是令所有点到拟合的曲线的距离之和最小。距离之和可表示为：
$$\begin{array}{l}\mathrm{L}(w,b)={\sum }_{i=1}^n{\left({\hat{y}}^i-\left(b+w\cdot x_{}^i\right)\right)}^2\end{array}$$
其中$n$ 为训练样本总数，${\hat{y}}^i$ 表示第$i$ 个样本的实际值，后面括号中的内容是我们训练的模型得出的值。

由于想要使得样本真实值与模型输出之间的距离最小化，我们可以写出下面的目标函数（也叫损失函数）：
$$\begin{array}{rl}{w}^{\ast },b^{\ast }& =\arg \underset{w,b}{\min }L(w,b)\\ & =\arg \underset{w,b}{\min }\sum _{i=1}^n{\left({\hat{y}}^i-\left(b+w\cdot x_{}^i\right)\right)}^2\end{array}$$上面的方法就叫做最小二乘法。
最小二乘法名字的由来有两点：

1. 使得训练集与拟合出的曲线误差最小
2. 令误差最小的方法是令所有点与拟合出的曲线距离之和最小

之所以采用平方的形式，是因为这样可以令所有误差为正值（不然正负误差会抵消）。

---

3. 线性回归的求解

上面这个损失函数有两种求解的方式，一种是利用线性代数直接求解，另外一种是利用梯度下降的方法求解。

3.1 利用线性代数求解

为便于公式的推导，这里先做一下改变，将线性模型表示为：
$$y={\mathbf{w}}^T\mathbf{x}$$或者考虑标量转置不变将上式写作：$$y={\mathbf{x}}^T\mathbf{w}$$其中$\mathbf{x}$ 与 $\mathbf{w}$ 均为向量，代表有多个变量影响表达式，把$b$ 也算在$\mathbf{w}$内，放在$\mathbf{w}$的第一项。
对所有样本来说，$b$对应的系数$x_0$恒定为1。

例如一元一次表达式可写作$\{\begin{array}{l}y=x_{0}b+x_{1}w\\ x_0=1\end{array}$，那么$\mathbf{w}=\left[\begin{array}{ll}{b}_{}& w_1\end{array}\right]$，$\mathbf{x}=[1x_1]$。

利用线性代数方法求解的推导：
$$\arg \underset{w,b}{\min }\sum _{i=1}^n{\left({\hat{y}}^i-\left(b+w^T\cdot x_{}^i\right)\right)}^2$$为方便紧凑表示去掉$\sum$号，使用$X=[x_{}^1{x}_{}^2\dots x_{}^n{]}^T$，使用$\hat{Y}=[{\hat{y}}^1{\hat{y}}^2\dots {\hat{y}}^n]$，

其中$X_{i,:}=x^{iT}$，$X\in R^{n\times (m+1)}$，$Y\in R^{(m+1)\times 1}$，$n$代表样本数，$m+1$代表每个样本的权重加上偏置的个数。
所以：
$$\arg \underset{w,b}{\min }\sum _{i=1}^n{\left({\hat{y}}^i-x_{}^{iT}\cdot w\right)}^2$$$$=\arg \underset{w,b}{\min }{\left(\hat{Y}-Xw\right)}^2$$$$=\arg \underset{w,b}{\min }{\left(\hat{Y}-Xw\right)}^T\left(\hat{Y}-Xw\right)$$$$=\arg \underset{w,b}{\min }\left({\hat{Y}}^T\hat{Y}-{\hat{Y}}^{T}Xw-w^T{X}^T\hat{Y}+w^T{X}^{T}Xw\right)$$想要满足上面的损失函数，只需令括号中的内容对$w$ 求导等于零即可。
$${\nabla }_w\left({\hat{Y}}^T\hat{Y}-{\hat{Y}}^{T}Xw-w^T{X}^T\hat{Y}+w^T{X}^{T}Xw\right)=0$$$$\Rightarrow 2X^{T}Xw=2X^{T}Y$$$$\Rightarrow X^{T}Xw=X^{T}Y$$$$\Rightarrow w={\left(X^{T}X\right)}^{-1}{X}^{T}Y$$

3.2 线性代数实现最小二乘法代码

import numpy as np
from matplotlib import pyplot as plt
# Training data
x_data = np.array([338., 333., 328., 207., 226., 25., 179., 60., 208., 606.])
y_data = np.array([640., 633., 619., 393., 428., 27., 193., 66., 226., 1591.])

# 初始化矩阵X和Y
X = x_data.reshape((len(x_data), -1))

# 将原始数据x_data转化为 m x (1+1) 的矩阵，1+1代表有两个系数b和w，m代表有m组数据
X = np.insert(X, 0, len(X)*[1], axis=1)
Y = y_data.T

# 根据w = (X^T·X)^{-1}·X^T·Y 来计算权重
# 权重向量weight，包含w 和 b，b放在第一项
weight = np.matrix(X.T.dot(X)).I.dot(X.T).dot(Y)

# 输出求出的权值
print(weight)

# 画图
plt.scatter(x_data, y_data)
x = np.linspace(0, 700, 700)
y = weight[0, 0]+weight[0, 1]*x
print(weight[0, 0], weight[0, 1])
plt.scatter(x, y)
plt.show()

效果：

---

3.3 利用梯度下降求解

  梯度下降法分别将权重$w$ 与偏移 $b$ 作为自变量，而样本中的$x$ 作为已知的系数，进而求出使得损失函数最小化的$w$ 与 $b$.
  寻常的讲，$x$应该是自变量，为什么我这里却说$w$ 与$b$ 是自变量呢？

  可以想象，由于$x$ 是训练的样本，其值是固定的，因此可以把$x$ 看作是系数，而变化的恰恰是$w$ 与 $b$，如果将这两个变化的值叫做变量的话，那么这两个变量的取值就直接影响了损失函数的大小。根据梯度下降的思想，就可以分别令损失函数对这两个变量进行偏微分，将计算出的结果整合在一起构成一个梯度向量。

  由于训练集的数据不止一个点，所以这里的梯度值采用的是${\sum }_{i=1}^{n}grad(w^i)$ 和 ${\sum }_{i=1}^{n}grad(b^i)$.也就是数据集中所有变量的梯度值之和。

---

3.4 梯度下降实现最小二乘法代码

# -*- coding:utf-8 -*-
import numpy as np
from matplotlib import pyplot as plt
# Training data
x_data = np.array([338., 333., 328., 207., 226., 25., 179., 60., 208., 606.])
y_data = np.array([640., 633., 619., 393., 428., 27., 193., 66., 226., 1591.])

# 画图
x = np.arange(-200, -100, 1)
y = np.arange(-5, 5, 0.1)
Z = np.zeros((len(x), len(y)))
X, Y = np.meshgrid(x, y)
for i in range(len(x)):
    for j in range(len(y)):
        b = x[i]
        w = y[j]
        Z[j][i] = 0
        for n in range(len(x_data)):
            Z[j][i] = Z[j][i] + (y_data[n] - b - w*x_data[n])**2
        Z[j][i] = Z[j][i]/len(x_data)
        

# 初始化参数
b = -120       # initial bias
w = -4         # initial weight
iterator = 100000
lr = 1  # learning rate

b_history = [b]
w_history = [w]

lr_w = 0
lr_b = 0


# 梯度下降
for i in range(iterator):
    b_grad = 0.0
    w_grad = 0.0
    for j in range(len(x_data)):  # sum(gradient)
        b_grad = b_grad - 2.0*(y_data[j]-w*x_data[j]-b)
        w_grad = w_grad - 2.0*(y_data[j]-w*x_data[j]-b)*x_data[j]

    # 使用adagrad优化
    lr_w = lr_w + w_grad ** 2
    lr_b = lr_b + b_grad ** 2
    b = b - lr / np.sqrt(lr_b) * b_grad
    w = w - lr / np.sqrt(lr_w) * w_grad

    b_history.append(b)
    w_history.append(w)


# 前面已经用线代方法算出标准答案，b=-188.4，w=2.67
# 这里黑线越逼近画出的标准答案，证明梯度下降效果越好
plt.contourf(x, y, Z, alpha=0.5, cmap=plt.get_cmap('jet'))
plt.plot([-188.4], [2.67], 'x', ms=12, markeredgewidth=3, color='orange')
plt.plot(b_history, w_history, 'o-', ms=3, lw=1.5, color='black')
plt.xlim(-200, -100)
plt.ylim(-5, 5)
plt.xlabel(r'$b$', fontsize=16)
plt.ylabel(r'$w$', fontsize=16)
plt.show()

效果：

4.多次线性回归

我们所要拟合的曲线可能是多元多次的（比如二次方程），同样可以用最小二乘法拟合。下面是代码和结果：

# -*- coding:utf-8 -*-
import numpy as np
from matplotlib import pyplot as plt
# target: argmin∑(yi-(w1x^2+w2x^3+b))


# gradient descent, using adagrad
def gradient_descent(x_data, y_data):
    w1, w2, b = 0., 0., 0.
    lr = 1.0
    lr_w1, lr_w2, lr_b = 0., 0., 0.
    epochs = 100
    for i in range(epochs):
        w1_grad, w2_grad, b_grad = 0., 0., 0.
        # print(len(x_data))
        for j in range(len(x_data)):
            temp = y_data[j]-w1*(x_data[j]**2)-w2*x_data[j]-b
            w1_grad += (-x_data[j]**2) * temp
            w2_grad += (-x_data[j]) * temp
            b_grad += (-1) * temp
        w1_grad /= len(x_data)
        w2_grad /= len(x_data)
        b_grad /= len(x_data)
        # adagrad
        lr_w1 += w1_grad ** 2
        lr_w2 += w2_grad ** 2
        lr_b += b_grad ** 2
        # gradient descent
        w1 -= lr/np.sqrt(lr_w1) * w1_grad
        w2 -= lr/np.sqrt(lr_w2) * w2_grad
        b -= lr/np.sqrt(lr_b) * b_grad
    return w1, w2, b


def generate_data():
    x = np.arange(-10, 10, 1)
    error = np.random.randn(20) * 1
    y = 2.3*(x**2) + 3.6*x + 2.8 + error
    return x, y


if __name__ == '__main__':
    x, y = generate_data()
    w1, w2, b = gradient_descent(x, y)
    ty = w1*(x**2) + w2*x + b
    print('w1 = ', w1, '\nw2 = ', w2, '\nb = ', b)
    plt.plot(x, y, 'bo')
    plt.plot(x, ty, 'r-')
    plt.show()