十大机器学习算法之支持向量机(一)
最新推荐文章于 2022-10-26 14:44:37 发布
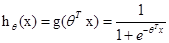
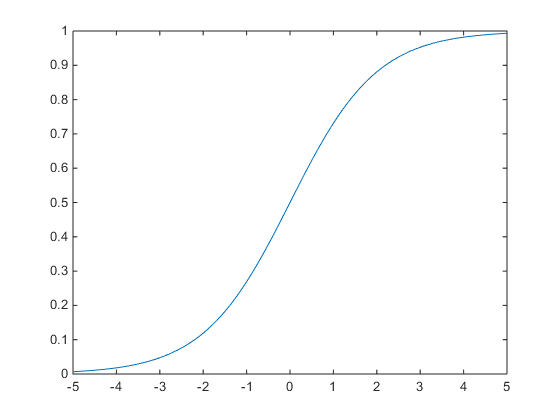
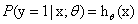
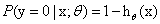
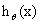 如果大于0.5,则特征就是属于y=1的类,反之,则是属于y=0的类。
如果大于0.5,则特征就是属于y=1的类,反之,则是属于y=0的类。 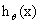 只与
只与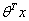 有关,
有关,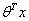 >0,那么
>0,那么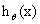 >0.5,g(z)只不过是用来映射的函数,真正的决定特征是属于哪一个类别的还是
>0.5,g(z)只不过是用来映射的函数,真正的决定特征是属于哪一个类别的还是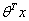 。可以看出当
。可以看出当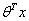 趋近于正无穷的时候,特征值是接近于1的,反之则是接近于-1。我们训练模型的目的就是希望训练数据中y=1的特征
趋近于正无穷的时候,特征值是接近于1的,反之则是接近于-1。我们训练模型的目的就是希望训练数据中y=1的特征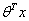 >>0,而y=0的特征远远小于0。Logistic回归的目的就是要学习得到这个θ,使得正例的特征远远大于0,负例的特征远远小于0,而且是要在所有的实例上达到这个训练目的。
>>0,而y=0的特征远远小于0。Logistic回归的目的就是要学习得到这个θ,使得正例的特征远远大于0,负例的特征远远小于0,而且是要在所有的实例上达到这个训练目的。 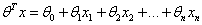 ,其中
,其中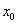 =1的。我们现在把
=1的。我们现在把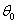 替换为b,其他的θ替换为w,替换后为:
替换为b,其他的θ替换为w,替换后为: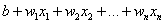 可以进一步简化为
可以进一步简化为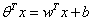 ,同时
,同时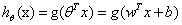 。也就是说最终y由y=0和y=1变为y=-1和y=1,只是这些标记数据变化之外。其他都没有什么区别。现在的假设函数为:
。也就是说最终y由y=0和y=1变为y=-1和y=1,只是这些标记数据变化之外。其他都没有什么区别。现在的假设函数为: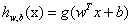 。上一小节我们说过只需要考虑
。上一小节我们说过只需要考虑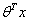 的正负问题,不用关心函数g(z)的大小变化,因此这里我们将g(z)做一个简化处理,把他简单的映射到-1和1上。映射关系如下所示:
的正负问题,不用关心函数g(z)的大小变化,因此这里我们将g(z)做一个简化处理,把他简单的映射到-1和1上。映射关系如下所示:
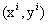 ,x是特征,y是标签,i标示第i个样本。
,x是特征,y是标签,i标示第i个样本。 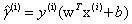
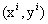 的函数间隔的最小值就是超平面关于训练样本集的函数间隔:
的函数间隔的最小值就是超平面关于训练样本集的函数间隔: 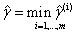
 =1的时候,在我们的g(z)中,
=1的时候,在我们的g(z)中,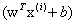 是大于等于0的,此时的函数间隔实际上就是
是大于等于0的,此时的函数间隔实际上就是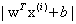 。为了使函数间隔最大(也就是确定样本是正例还是反例的确信度最大化),当
。为了使函数间隔最大(也就是确定样本是正例还是反例的确信度最大化),当 =1时,
=1时,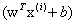 应该是一个极大数(是一个绝对值极大的数)。因此,函数间隔代表了我们认为特征是正例还是反例的置信度。
应该是一个极大数(是一个绝对值极大的数)。因此,函数间隔代表了我们认为特征是正例还是反例的置信度。 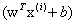 最大化,我们可以试着同时按照比例增大w和b的值(比如2w,2b)则这个时候的函数间隔变为原来的2倍,但是超平面并没有发生变化,所以,这个函数间隔是由BUG存在的,只是使用这一个来定义远远不够,这个时候就要我们的几何间隔出面了。
最大化,我们可以试着同时按照比例增大w和b的值(比如2w,2b)则这个时候的函数间隔变为原来的2倍,但是超平面并没有发生变化,所以,这个函数间隔是由BUG存在的,只是使用这一个来定义远远不够,这个时候就要我们的几何间隔出面了。 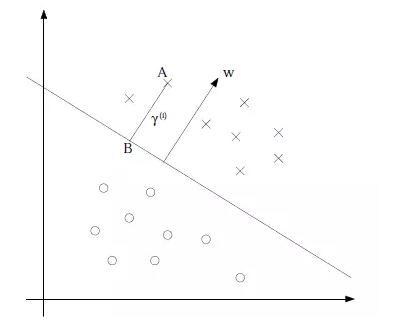
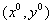 点,其垂直投影到超平面的对应点为B,w是垂直于超平面的一个向量,r为样本点A到超平面的距离,此时有单位向量为
点,其垂直投影到超平面的对应点为B,w是垂直于超平面的一个向量,r为样本点A到超平面的距离,此时有单位向量为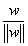 ,所以B点的坐标为
,所以B点的坐标为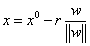 (利用几何知识计算),带入到超平面
(利用几何知识计算),带入到超平面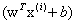 =0得到:
=0得到: 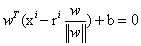
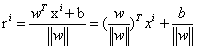
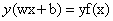 实际上就是f(x),只是认为定义的间隔度量,而几何间隔f(x)/||w||才是直观上的点到超平面的距离。
实际上就是f(x),只是认为定义的间隔度量,而几何间隔f(x)/||w||才是直观上的点到超平面的距离。 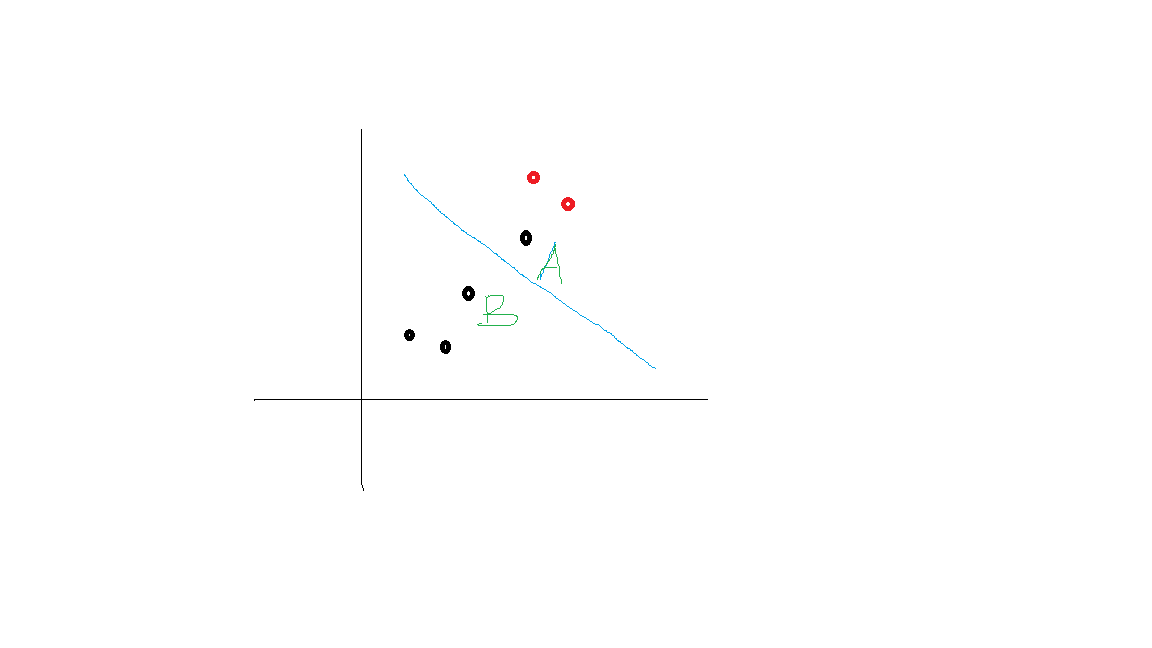 就是图中A点和B点离超平面的距离最大化。
就是图中A点和B点离超平面的距离最大化。 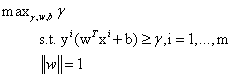
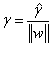 ,我们把上面等式重新换个方式写出来:
,我们把上面等式重新换个方式写出来: 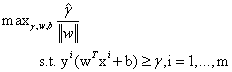
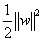 的最小值,因此,改写之后的结果为:
的最小值,因此,改写之后的结果为: 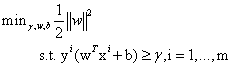
 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


