使用快排解决TOP K的时间复杂度分析

一、TOP K问题

TOP K问题就是在一堆数据里面找到前 K 大的数。

二、算法

1.快排

设输入数组如下

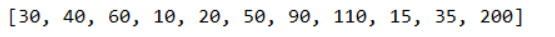
我们把最大的K个数放在后面。

快排每次把选中的基准数放到它应该在的位置，然后它的左侧的数都比它小，右侧的数都比它大。

代码如下：

public static void Sort(int[] a, int l, int r) {
        if (l < r) {//如果l小于r了，说明已经完成这段排序将会直接返回
            int i,j,pivot;
            i = l;
            j = r;
            pivot = a[i];//选择值
            while (i < j) {
                while(i < j && a[j] > pivot)
                    j--; // 从右向左找第一个小于pivot的数
                if(i < j)
                    a[i++] = a[j];
                while(i < j && a[i] < pivot)
                    i++; // 从左向右找第一个大于pivot的数
                if(i < j)
                    a[j--] = a[i];
            }
            a[i] = pivot; //pivot已被排好序
            Sort(a, l, i-1); /* 递归半区排序 */
            Sort(a, i+1, r); /* 递归半区排序 */
        }
    }

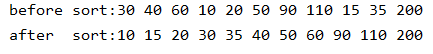
2.TOPK版

TOP K问题中，我们只需要找出最大的几个数，但是不需要对它们进行排序。

比如,我们需要最大的4个数，令k=4。如上图所示，我们的基准数如果一开始恰好就选中了那个本应该排在第七个的数50，那么一次排序后，左侧的数都比50小，得到右侧4个比50大的数，TOP K问题就解决了。

比起快排，TOP K代码不需要两边都排序，因此在快排基础上只需要加个半区判断即可：

 private static void solution(int[] a, int l, int r,int k) {
        int i=l,j=r,pivot=a[i];
        while (i<j){
            while (i<j&&a[j]>pivot)
                j--;
            if (i<j)
                a[i++]=a[j];
            while (i<j&&a[i]<pivot)
                i++;
            if (i<j)
                a[j--]=a[i];
        }
        a[i]=pivot;
        if (i==a.length-1-k)
            return;
        else if (i<a.length-1-k)
            solution(a, i+1, a.length-1,k);
        else
            solution(a, 0, i-1,k);
    }

---

三、复杂度分析

首先看快排

最优的时候，每次pivot都恰好选在了中间，两个递归区间长度相同，此时时间复杂度为
$$\begin{array}{c}T(n)=n+2\ast T\left(\frac{n}{2}\right)=n+2\ast \left(\frac{n}{2}\right)+2\ast 2\ast T\left(\frac{n}{2\ast 2}\right)+\cdots +n+T(1)\\ T(n)=n\log n\end{array}$$
最糟糕的时候，每次pivot都选的是排序后最边上的值，这时候的复杂度为
$$\begin{array}{c}T(n)=n^2\end{array}$$
平均情况下，每种可能性我们都考虑进去，出现的概率为$\frac{1}{n}$,则复杂度计算公式为
$$T(n)=n+\frac{1}{n}\sum _{i=1}^n(T(i-1)+T(n-i))$$
考虑到和式的对称性, 所以
$$T(n)=n+\frac{2}{n}\sum _{i=0}^{n-1}T(i)$$
接下来解递推公式得到
$$T(n)=n\log n$$

接下来分析TOP K下的复杂度

最好的时候，我们每次选到中间，因为每次选完后只需要对其中一部分进行处理, 因此
$$T(n)=n+T\left(\frac{n}{2}\right)=n+\frac{n}{2}+2\ast T\left(\frac{n}{2}\right)+\cdots$$
由等比数列求和易知
$$T(n)=n$$
最糟糕的时候, 同样是每次我们都选到了最边上, 这时候每次选择后减少的处理次数也派不上用场，复杂度退化到
$$T(n)=n^2$$
平均情况下，对比快排复杂度计算的式子
$$T(n)=n+\frac{1}{n}\sum _{i=0}^{n-1}T(i)$$
此时前面的 $\mathrm{n}$ 受划分情况的影响，比如，第一次消耗为n，假设第一次刚好选择了中间的值，第二次处理其中一半即可，即$\frac{n}{2}$。假设第一次刚好选择了最边缘的值，第二次还是需要消耗n-1。

因此前面的 $\mathrm{n}$ 受划分情况的影响
$$T(n)=\frac{1}{n}\sum _{i=0}^{n-1}(i+T(i))$$
令
$$T(n+1)=\frac{1}{n+1}\sum _{i=0}^n(i+T(i))$$
得到
$$(n+1)T(n+1)-nT(n)=T(n)+n$$
这里直接代入法求解就行了
$$T(n)=n$$