矩阵乘法+快速幂加速DP

前段时间线代才学完矩阵，这就可以用上了！不得不说线代还是非常有用的，矩阵乘法在计算机图形学里也很有用，高斯消元求方程组也是很常用，瞬间对线代感兴趣了！

引入

求斐波那契数列第n项

首先，我们回忆一个简单的问题：求斐波那契数列的第n项。
这个问题很简单，假设我们用f[i]来表示，那么
f[1]=f[2]=1
f[i]=f[i-1]+f[i-2](i>=2)
这应该也算是dp问题吧，虽然这题很简单。

快速幂

接下来，我们回忆一下整数的快速幂：
对于a^b，我们可以把b看作一个二进制数，然后通过对a反复平方并选择需要的部分乘在一起来拼凑出a^b。这样讲很抽象，举个例子，对于5²³，很明显，它等于5^1+2+4+16，然后我们先定义一个res来存储我们的答案，我们就能写出如下代码：

int res=1,b=23,a=5;
while(b){
	if(b&1) res*=a;
	b>>=1;
	a*=a;
}

b（即23）的二进制表示为10111，因此第一次循环时res会累乘上a，然后b右移一位，a自乘变为a²，而第四次循环b的最低位为0，res不会累乘上a⁸，a还是要自乘，因为下一位为1，需要乘上a¹⁶，这样直到b为0，自己模拟一遍就会理解我们做了什么。

矩阵乘法+快速幂求斐波那契数列第n项

好，回忆玩上面的内容我们就将进入今天的正题，还是求斐波那契数列的第n项，当n达到20亿的级别时，我们还能通过递推很快的求出来吗？显然不能，这时候一种神奇的做法就出现了。



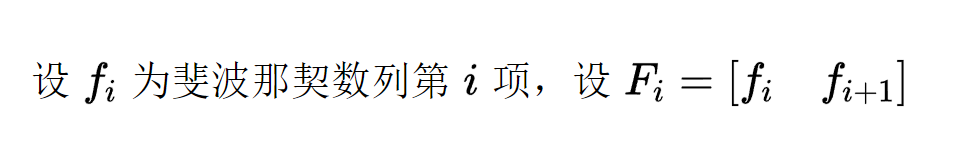
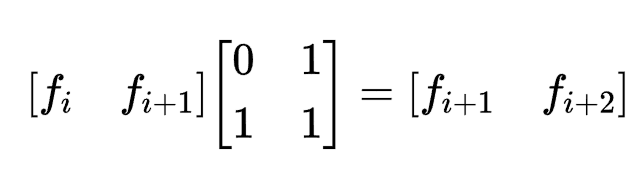
那么我们只需要先对矩阵A^n-1求快速幂，然后再与F₁相乘，得到矩阵的第一个数就是答案了。这是一个非常大的优化，时间复杂度从O(n)降到O(log n)。代码实现我就懒得写了，后面应用的题目里面有差不多的，可以看那里的代码。
注意:这里A矩阵一定要不含变量，否则我们无法使用快速幂求解（这应该很好理解吧）

应用

斐波那契前n项和

题目链接：1303.斐波那契前n项和
对于这道题，我们发现我们还需要求前n项和，这是再只用两个变量就不够了，因此我们需要多加一个变量。

于是F_n=F₁A^n-1，代码实现：

#include<iostream>
#include<cstring>
using namespace std;
typedef long long LL;
int n,m;
void mul(int c[3][3],int a[3][3],int b[3][3]){
    int tmp[3][3]={0};
    //这里我们要开一个临时数组存储答案，因为a、b、c中可能有指向相同位置的情况，先把答案存储在临时数组中更保险
    for(int i=0;i<3;i++)
        for(int j=0;j<3;j++)
            for(int k=0;k<3;k++)
                tmp[i][j]=(tmp[i][j]+(LL)a[i][k]*b[k][j])%m;
    memcpy(c,tmp,sizeof tmp);//答案赋值回c
}
int main(){
    cin>>n>>m;
    int f1[3][3]={1,1,1};//即F1矩阵
    /*
    为什么f1开成二维数组呢？因为我们a*a是两个3*3的矩阵相乘
    而如果f1是一维的话，我们还需要额外实现一个1*3的矩阵与
    3*3的矩阵相乘的函数，把f1开成二维，因为后两行数都为0
    所以不影响最终答案
    */
    int a[3][3]={//即A矩阵
        {0,1,0},
        {1,1,1},
        {0,0,1}
    };
    n--;//我们需要求a的n-1次方，n先--就行了
    while(n){
        if(n&1) mul(f1,f1,a);//f1=f1*a
        n>>=1;
        mul(a,a,a);//a=a*a;
    }
    cout<<f1[0][2]<<endl;
    return 0;
}

佳佳的斐波那契

题目链接：1304.佳佳的斐波那契
很明显，对于这一题，我们需要的变量更多了，我们先推导一下公式：



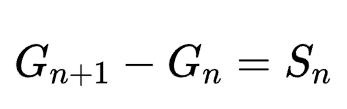
这样，我们就可以用矩阵快速幂求出A_n，而最终要求的T_n，就等于nS_n-G_n
代码实现：

#include<iostream>
#include<cstring>
using namespace std;
typedef long long LL;
int n,m;
int tmp[4][4];
void mul(int c[4][4],int a[4][4],int b[4][4]){
    memset(tmp,0,sizeof tmp);
    for(int i=0;i<4;i++)
        for(int j=0;j<4;j++)
            for(int k=0;k<4;k++)
                tmp[i][j]=(tmp[i][j]+(LL)a[i][k]*b[k][j])%m;
    memcpy(c,tmp,sizeof tmp);
}
int main(){
    cin>>n>>m;
    int f1[4][4]={1,1,1,0};
    int a[4][4]={
      {0,1,0,0},
      {1,1,1,0},
      {0,0,1,1},
      {0,0,0,1}
    };
    int k=n-1;//因为我们后面还会用到n，所以这里再开一个k
    while(k){
        if(k&1) mul(f1,f1,a);//f1=f1*a;
        mul(a,a,a);//a=a*a;
        k>>=1;
    }
    cout<<(((LL)n*f1[0][2]-f1[0][3])%m+m)%m<<endl;
    return 0;
}

GT考试

题目链接：GT考试
这题是真的算法竞赛难度了，对于这样的问题我们肯定首先考虑动态规划，我们假设f[i][j]表示长度为i，不包含不吉利串，末尾部分（即后缀）与不吉利数字前缀相同的长度是j的字符串的数量，当我们考虑状态f[i][j]的转移时，我们在这i位后面追加一位，假设此时它的后缀与不吉利数字的前缀相同的长度变为k，那么f[i+1][k]+=f[i][j]，因此我们可以得到公式（这里用f(i,j)表示f[i][j]）:

本图来源：GT考试题解
其中a_i,j表示与不吉利串的前i位匹配、加上一位后匹配的长度，这里我们可以用kmp求解。这里为什么没有f(i+1,m)呢？因为匹配长度为m时就包含不吉利串了，不合题意。然后我们发现：

关于F₀中各项数字为什么是这样？需要结合题意和实际元素来分析，这里留给读者思考。最终F_n中的元素即为f(n,0)~f(n,m-1)，求一下和就得到答案了。
代码实现：

#include<iostream>
#include<cstring>
using namespace std;
const int N=25;
int a[N][N],ne[N],n,m,mod,f[N][N],tmp[N][N];
char s[N];
void mul(int c[N][N],int a[N][N],int b[N][N]){
    memset(tmp,0,sizeof tmp);
    for(int i=0;i<m;i++)
        for(int j=0;j<m;j++)
            for(int k=0;k<m;k++)
                tmp[i][j]=(tmp[i][j]+a[i][k]*b[k][j])%mod;
    memcpy(c,tmp,sizeof tmp);
}
int qmi(int k){
    while(k){
        if(k&1) mul(f,f,a);
        mul(a,a,a);
        k>>=1;
    }
    int res=0;
    for(int i=0;i<m;i++) res=(res+f[0][i])%mod;
    return res;
}
int main(){
    f[0][0]=1;
    cin>>n>>m>>mod;
    cin>>s+1;
    for(int i=2,j=0;i<=m;i++){//kmp模板
        while(j&&s[j+1]!=s[i]) j=ne[j];
        if(s[j+1]==s[i]) j++;
        ne[i]=j;
    }
    for(int i=0;i<m;i++)//枚举已经匹配的长度
        for(int j='0';j<='9';j++){//枚举追加的字符
            int k=i;
            while(k&&s[k+1]!=j) k=ne[k];
            if(s[k+1]==j) k++;
            a[i][k]++;
        }
    cout<<qmi(n)<<endl;
    return 0;
}

做完这题，感觉我的kmp又有所进步，呵呵 。KMP我不知道复习了多少遍，遇到题目还是不会，呵呵 。