长文阅读】MAMBA作者博士论文＜MODELING SEQUENCES WITH STRUCTURED STATE SPACES＞-Chapter4 HIPPO

Chapter 4 HIPPO: Continuous Memory with Optimal Polynomial Projections

Gu A. Modeling Sequences with Structured State Spaces[D]. Stanford University, 2023.

本文是MAMBA作者的博士毕业论文，为了理清楚MAMBA专门花时间拜读这篇长达330页的博士论文，由于知识水平有限，只能尽自己所能概述记录，并适当补充一些相关数学背景，欢迎探讨与批评指正。内容多，分章节更新以免凌乱。

本章主要讨论了一种名为HIPPO（High-order Polynomial Projection Operators）的框架，用于处理序列数据中的记忆问题。HIPPO通过在线函数近似来处理记忆，将函数的最佳系数存储为基函数的形式。这种方法特别强调正交多项式的使用，因为它们的最佳系数可以闭式表示。此外，该框架利用不同的度量来生成适应不同时间尺度的序列数据处理方法，并提供理论保证。文章还展示了HIPPO框架在处理长期依赖性、计算效率、梯度流动和近似误差方面的理论和实验优势。总的来说，这部分内容深入探讨了记忆表示问题，并提出了一种新的方法来有效处理复杂的时间序列数据。

备注 ：为了强调与 SSM 的独立性，本章的材料使用不同的符号：使用 $f(t)$ 表示输入函数， 代替 $u(t)$ 表示输入。使用 $c(t)$表示“多项式系数”的状态，这是最初发表的 HIPPO 论文中的注释。

4.1 Introduction

本节讨论了顺序数据建模和学习的基本问题，这些问题包括语言建模、语音识别、视频处理和强化学习。核心是如何建立长期复杂时间依赖的模型，即如何存储和整合过去时间步骤的信息。传统方法是模拟随时间演变的状态。长距离依赖建模的核心问题是如何通过有限的memory来尽可能记住之前所有的历史信息。当前的主流序列建模模型（即Transformer和RNN) 存在着普遍的遗忘问题。

• fixed-size context windows: Transformer的window size通常是有限的，一般来说quadratic的attention最多建模到大约10k的token就到计算极限了
• vanishing gradient: RNN通过hidden state来存储历史信息，理论上能记住之前所有内容，但实际上的effective memory大概是<1k个token的level，可能的原因是gradient vanishing

4.2 High-order Polynomial Projection Operators

这部分内容其实就是NIPS’2020论文：HiPPO: Recurrent Memory with Optimal Polynomial Projections的一部分。

第4.2节“高阶多项式投影算子”（High-order Polynomial Projection Operators）中，介绍了在线函数近似问题的概念和HIPPO框架的总体思路。这一部分详细讨论了如何使用多项式基函数来近似一个函数，并在不同时间点维护这个近似的最优系数。文档描述了HIPPO框架的技术细节，包括如何选择适当的基函数集合和度量，以及如何使用这些基函数来优化近似过程。此外，还探讨了将这种连续时间的思想转化为实际应用中的离散时间版本的方法。最后，展示了如何将HIPPO框架应用于RNN中的记忆机制，提供了关于不同度量和优化策略的深入分析，并讨论了这种方法的理论保证和实际应用效果。

4.2.1 HIPPO Problem Setup

为了了解迄今为止所看到的输入并做出未来的预测，由于函数空间极其庞大，历史无法完美记忆，必须进行压缩；论文提出将其投影到有界维子空间的一般方法。因此，目标是（在线）维护历史的压缩表示。为了充分说明这个问题，需要两个要素：量化近似的方法和合适的子空间。

问题

考虑一个一维函数，我们能否用一个固定大小的representation $c(t)\in {\mathbb{R}}^N$ 来最优拟合 $f$ 在$[0,t]$(后面记作 $f_{\le t}$) 的曲线？ 并且随着$t$的增加，例如从 $t_1$ 到 $t_2$ ，我们可以在线的根据 $c\left(t_1\right)$ 求$c\left(t_2\right)$ 来拟合 $f_{\le t_2}$ ？

如何判断拟合的质量

我们需要一个测度(measure)来判定拟合出来的连续函数和原来的连续函数的相似度 （ in other words, how much we care about every time in the past，对不同的time step $x$有着一个权重 $\mu (x)$ ）。 每个measure都需要在函数空间里定义一个距离， 即定义函数的内积：$⟨f,g{⟩}_{\mu }={\int }_0^{\infty }f(x)g(x)\mathrm{d}\mu (x)$

如何用N维向量来编码 $f_{\le t}$

假设一组多项式正交基 G = { g n } n < N \mathcal{G}=\left\{g_{n}\right\}_{n<N} G={gn​}n<N​ 满足${⟨g_i,g_j⟩}_{\mu }=0$（注意到正交基是由测度$\mu$决定的，不同的 $\mu$ 对应不同的 $\mathcal{G}$ ）。我们直接把 $f_{\le t}$ 投影到多项式正交基 $\mathcal{G}$ 上，让每个投影分量为$c(t)$的分量：

$c_n^{(t)}:={⟨f_{\le t},g_n⟩}_{{\mu }^{(t)}}$

也就是说 $c(t)$是多项式正交基的系数向量 （类似于傅立叶变换后的频域的值）

然后是论文中的描述：

函数近似与度量（Function Approximation with respect to a Measure）:通过在 $[0,\infty )$ 上的任何概率度量 $\mu$ 来实现的。这个度量为平方可积函数空间提供了内积，进而导致一个希尔伯特空间结构（${\mathcal{H}}_{\mu }$以及相应的范数$\Vert f{\Vert }_{L_2(\mu )}=⟨f,f{⟩}_{\mu }^{1/2}$）。

多项式基展开：在此基础上，可以选择任何 $N$ 维子空间作为近似的候选，其中 $N$ 是近似的阶数或压缩大小。论文认为，多项式基是一种自然的选择，使得$\mathcal{G}$成为度数小于 $N$ 的多项式集合。

在线近似：由于我们关心每个时间 $t$ 的近似 $f_{\le t}$，因此还要让度量随时间变化。对于每个 $t$，令 ${\mu }^{(t)}$ 为 $[0,\infty )$ 上支持的测度（因为$f_{\le t}$仅在时间 $t$ 之前定义）。寻求$g^{(t)}\in \mathcal{G}$ 来最小化${\Vert f_{\le t}-g^{(t)}\Vert }_{L_2\left({\mu }^{(t)}\right)}$ 。直观上，测度$\mu$控制着输入域各部分的重要性，而定义了允许的近似值。挑战在于如何以闭式解决优化问题，形成给定的 ${\mu }^{(t)}$，以及如何在 $t\to \infty$ 时在线维护这些系数。

4.2.2 General HIPPO framework

本小节介绍了HIPPO框架的主要理念和解决问题的策略。这个框架基于正交多项式和信号处理文献中相关变换的丰富历史。在HIPPO框架中，对于一个输入函数$f(t)$，使用正交多项式基来表示它的近似，并且根据时间变化的度量${\mu }^{(t)}$动态更新这些系数。论文还提到了如何通过不同的时间变化度量，使用HIPPO框架对任意函数进行投影操作。重点在于如何在线维护这些系数，使其可以随时间递增更新，从而实现函数的高效在线近似。此外，还讨论了这个框架的一些理论优势，包括对输入时间尺度的不变性、更新的效率和近似误差的界限

HIPPO 抽象：在线函数逼近

定义 4.1：给定 $(-\infty ,t]$ 支持的时变测度族 ${\mu }^{(t)}$、多项式的 $N$ 维子空间 $\mathcal{G}$ 和连续函数 $f:{\mathbb{R}}_{\ge 0}\to \mathbb{R}$，HIPPO 定义投影算子 ${proj}_t$ 和系数提取算子 ${coef}_t$ ，在每个时间 $t$ 的具有以下属性：

(1) ${proj}_t$ ：将函数 $f$ 限制到时间 $t$，$f_{\le t}:={f(x)|}_{x\le t}$，并将其映射到多项式 $g^{(t)}\in \mathcal{G}$，从而最小化近似误差 ${\Vert f_{\le t}-g^{(t)}\Vert }_{L_2\left({\mu }^{(t)}\right)}$。

(2) ${coef}_t$ : $\mathcal{G}\to {\mathbb{R}}^N$ 将多项式 $g^{(t)}$ 映射到相对于度量${\mu }^{(t)}$定义的正交多项式基的系数 $c(t)\in {\mathbb{R}}^N$。这意味着 $g^{(t)}$ 的表示是通过其在这组正交多项式基上的系数来进行的。这种映射对于在线函数近似的过程至关重要，因为它提供了一种方法来动态地表示和更新函数的近似，这是根据随时间变化的度量来实现的。

HIPPO 操作符:$\text{ coef o proj }$,是一个由两个步骤组成的复合操作，首先是 proj，它将一个函数$f:{\mathbb{R}}_{\ge 0}\to \mathbb{R}$映射到其在多项式基上的投影，然后是 coef，它将这个投影转换成对应的最优投影系数 $c:\mathbb{R}\ge 0\to {\mathbb{R}}^N$。简单来说，Hippo(f) 表示的是计算函数 $f$ 在每个时间点 $t$ 的最优多项式投影系数，是一种将函数映射到其在正交多项式基上系数的方法。

系数函数 $c(t)={\mathrm{coef}}_t\left({\mathrm{proj}}_t(f)\right)$ 具有 ODE 的形式，对于某些 $\mathbf{A}(t)\in {\mathbb{R}}^{N\times N}$ 满足 $c^{\prime }(t)=\mathbf{A}(t)c(t)+\mathbf{B}(t)f(t)$,$\mathbf{A}(t)\in {\mathbb{R}}^{N\times N},\mathbf{B}(t)\in {\mathbb{R}}^{N\times 1}$。因此，结果展示了如何通过求解 ODE，或更具体地通过运行离散递推来在线轻松获得 $c(t)$。离散化时，HIPPO 接收一系列实值并生成一系列 $N$ 维向量。

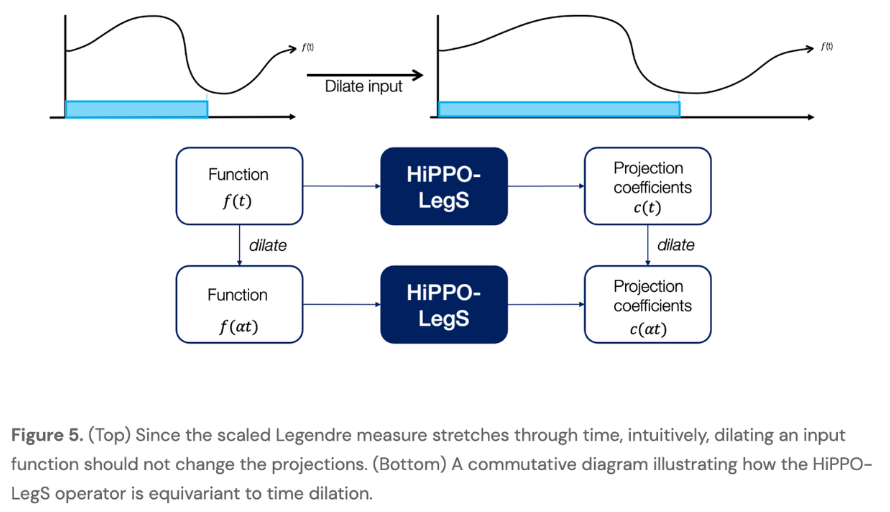
对上面的图再理解一下：上图中输入函数$f(t)$（黑线）通过存储其最佳多项式投影的系数（彩色线）来持续逼近，这些系数根据指定的度量（彩色框）进行存储。这些系数会随着时间的推移而演变（红色、蓝色），遵循常微分方程。从离散的角度来理解的话，我们从 $t=0$ 开始，每次给一个输入 $f(t)$ ，然后来更新$c(t)$ 用来编码$f_{\le t}$ ，接着再输入 $f(t+1)$ 并更新 $c(t+1)$来编码 $f_{\le t+1}$ 。可以看出， $f(t+1)$ 的值受 $c(t)$ 和 $f(t+1)$ 的影响，那么 $c(t+1)$ 可以写成 $c(t)$ 和 $f(t+1)$ 的函数 （类似RNN）。 HiPPO证明，在连续的情况下，这个过程可以用一个一阶ODE来建模：$\dot{c}(t)=A(t)c(t)+B(t)f(t)$。只要给定测度$\mu$ 我们就能确定 $A\in {\mathbb{R}}^{N\times N},B\in {\mathbb{R}}^{N\times 1}$ 。如果按着这个ODE的dynamics走的话, $c(t)$ 就是我们要找的最优编码 $f_{\le t}$ 的coefficient，如上图。

4.2.3 High Order Projection: Measure Families and HIPPO ODEs

这一小节专注于自然滑动窗口度量及其对应的投影算子的例子，并以此重现了Legendre Memory Unit（LMU）。同时，这一节还分析了LMU的局限性。特别地，提到了转换Legendre（LegT）度量，该度量对最近历史给予均匀权重，并且引入了一个控制滑动窗口长度的超参数$\theta$。文中提出了一个关于LegT的定理，并用线性时不变的常微分方程来描述这种情况，从而证明了LMU更新规则。此外，还讨论了这种滑动窗口更新规则的一个额外近似源。

只要给定measure，整个$c(t)$的dynamics就是确定的，下面是两个具体measure的例子

4.2.4 HIPPO Recurrences: from Continuous- to Discrete- Time

本小节描述如何将连续时间的HIPPO（高阶多项式投影算子）操作转换为离散时间的线性递归。这个转换对于将HIPPO框架应用于实际的序列和时间序列数据至关重要，因为实际数据通常是离散的。在连续情况下，这些运算符消耗输入函数 $f(t)$ 并产生输出函数 $c(t)$。离散时间情况 (i) 消耗输入序列 ${\left(f_k\right)}_{k\in \mathbb{N}}$，(ii)隐式定义函数 $f(t)$，其中 $f(k\cdot \Delta )=f_k$ 对于某个步长 $\Delta$，(iii) 通过 ODE 动力学生成函数 $c(t)$，并且 (iv) 离散化回输出序列$c_k:=c(k\cdot \Delta )$。

4.2.5 Low Order Projection: Memory Mechanisms of Gated RNNs

本小节探讨了当在投影问题中不包含高阶多项式时会发生什么。具体来说，如果N=1（即使用一阶多项式），HIPPO-LegT的离散化版本就变为一个门控循环神经网络（Gated RNN）。文中指出，与HIPPO使用单一隐藏特征并将其投影到高阶多项式不同，这些模型使用许多隐藏特征，但仅使用一阶多项式进行投影。这种观点揭示了这些经典技术的内在逻辑，说明了它们是如何从基本原理中推导出来的。例如，通过并行堆叠多个单元并选择特定的更新函数，可以特别得到GRU更新单元作为一个特例。

4.3 LegS: Scaled Measures for Timescale Robustness

介绍了一种新的记忆机制——缩放勒让德度量（LegS）。LegS 通过对整个历史赋予均匀的权重，来解决记忆过程中的时标问题。这一节证明了HIPPO-LegS的理论性质，包括输入时标的不变性、快速计算性、以及梯度和逼近误差的界限。LegS不需要任何有关时标的超参数，这使得它能够适应不同输入时标。此外，相较于具有超参数$\theta$的LegT度量，LegS在理论和实践上显示出了更好的时标鲁棒性。这一节通过新的度量设计，提出了一个更加健壯和理论上可靠的记忆机制。

HIPPO-LegS连续性和离散型的两种形式：

4.4 Empirical Validation

这一部分通过几个实验来验证HIPPO框架，包括在线函数近似和速度基准测试。文中展示了HIPPO-LegS能够处理数百万时间步长的依赖关系，并且其内存更新在计算上高效。此外，对不同离散化方法进行了函数近似错误分析，证明了HIPPO-LegS在各种离散化方法下的有效性。最后，还验证了HIPPO-LegS在面对不同时间尺度数据时的鲁棒性，特别是在处理时间序列分类任务时对抽样率变化的适应性。这一部分证实了HIPPO理论的可行性和实用性。

LegS的三大好处

• Gradient bounds： RNN对历史信息的遗忘速度是指数级的，HiPPO的遗忘速度是多项式级，好处就是可以用来建模更长的sequence同时尽可能不遗忘

• Computational efficiency: $A_t$ 有特殊的结构， 因此recurrence可以在linear而不是quadratic time算出

• Timescale robustness： 缩放的度量与输入函数的快速演变无关

有什么好处呢？表格显示了在轨迹分类数据集上的结果，训练序列和测试序列之间存在分布偏移（即由于时间序列在部署时以不同速率采样而产生的）；HiPPO 是唯一能够推广到新时间尺度的方法！

潜在的应用：低分辨率训练vision model, 可以较为无损的迁移到高分辨率

4.5 Conclusion

第四章通过提出一个框架（HIPPO），解决了序列数据中记忆的根本问题。HIPPO的核心是最优函数近似的抽象概念，这一概念是针对随时间变化的度量来定义的。除了统一并解释现有的记忆方法外，HIPPO还推出了一种新方法（HIPPO-LegS），这是朝向时标鲁棒性迈出的第一步，能够有效处理数百万时间步的依赖关系。HIPPO在历史上早于用于深层序列建模的结构化状态空间模型（SSM，例如S4）；接下来的两章将从SSM的角度描述它，并将其与第一部分连接起来。