HDU 1693 Eat the Trees （插头DP，闭合路径）

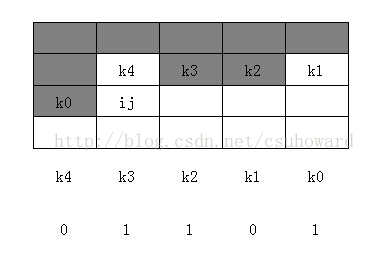
之前对于经典骨牌的轮廓线DP的位压缩，采用的如下形状的位压缩：

当ij判断放置哪种骨牌时，是根据k4k3k2k1k0判断的，在填入了骨牌后，转移到的状态也是由k3k2k1k0ij这样排布的，就是原状态左移一下，如果横着放骨牌就会影响到k0位，竖着放和不放都是把ij从右边附加到原状态上。

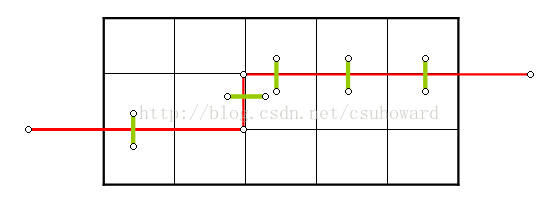
本题的插头DP是保存插头的状态，采用如下的状态：

红线就是轮廓线，轮廓线上有插头。有插头就记为1，没有插头就记为0。上图就是k0k1k2k3k4k5=101111。竖的红线右侧就是当前位ij。

初始状态当然是一个插头都没有就是k0k1k2k3k4k5=000000，结束状态也是000000。

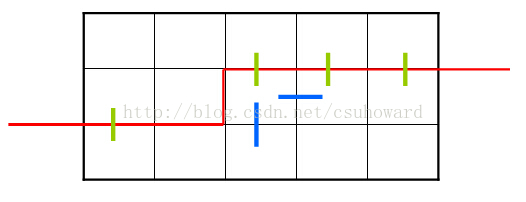
转移时只要判当前格子（本图为第二行第三列的格子，当前状态是101111）左插头和上插头的状态，就能知道能够转移到哪些状态去。

现在就转移到了100011这种状态。

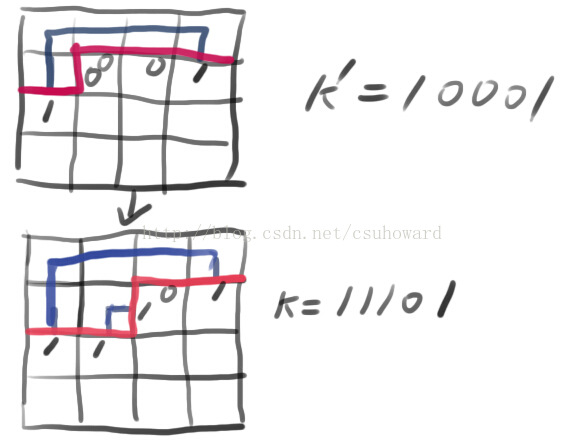
假如知道现在的状态，也可以通过先前的状态推得现在状态组数。

枚举现在的状态，枚举到第2行第2列的11101状态（我的状态左边是低位，11101存的时候就按10111存），当前状态可以由第2行第1列的10001转移得到。

其实用滚动数组可以只保存2*（1<<12）个状态就够了，时间复杂度为n*m*(1<<m)。

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;

typedef long long LL;
int const maxn = 12;
int g[maxn][maxn];
LL dp[2][1<<maxn];
int n,m;

void read(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            scanf("%d",&g[i][j]);
        }
    }
}

LL solve(){
    read();
    int cur=0;
    memset(dp,0,sizeof dp);
    dp[cur^1][0]=1;
    for(int i=1;i<=n;i++){
        memset(dp[cur],0,sizeof dp[cur]);
        for(int k=(1<<m)-1;k>=0;k--){
            dp[cur][k<<1]=dp[cur^1][k];
        }
        cur^=1;
        for(int j=1;j<=m;j++,cur^=1){
            int b=1<<(j-1);
            int r=1<<j;
            for(int k=(1<<(m+1))-1;k>=0;k--){
                if(g[i][j]){
                    if(j!=m){
                        if((r&k) && (b&k)){//下方和右方都有插头
                            dp[cur][k]=dp[cur^1][k^b^r];
                        }else if((r&k) || (b&k)){//下方或右方一方有插头
                            dp[cur][k]=dp[cur^1][k]+dp[cur^1][k^b^r];
                        }else{//下方和右方都没插头
                            dp[cur][k]=dp[cur^1][k^b^r];
                        }
                    }else if(!(r&k)){
                        if(b&k){
                            dp[cur][k]=dp[cur^1][k]+dp[cur^1][k^b^r];
                        }else{
                            dp[cur][k]=dp[cur^1][k^r^b];
                        }
                    }else{
                        dp[cur][k]=0;
                    }
                }else{
                    if((r&k)||(b&k)){//下方或右方有插头
                        dp[cur][k]=0;
                    }else{//没有插头
                        dp[cur][k]=dp[cur^1][k];
                    }
                }
            }
        }
    }
    return dp[cur^1][0];
}

int main(){
    int T;
    LL ans;
    scanf("%d",&T);
    for(int cas=1;cas<=T;cas++){
        ans = solve();
        printf("Case %d: There are %I64d ways to eat the trees.\n",cas,ans);
    }
    return 0;
}