线形对象与平面相交

三维空间中的线形对象包括直线、射线和线段，为了统一三者的表达，在三维图形学中一般使用一个点和方向向量的方式来描述这些线形对象。

假设有一个点P位于线形对象上，方向向量是$\vec d$，那么这个线形对象可以使用下面的公式来表达：

$$L(t) = P + t \vec d$$

基于这个表达式，直线方程可以描述为：

$$L(t) = P + t \vec d \quad ( -\infty \le t \le \infty)$$

射线方程可以描述为（P是射线的端点）：

$$R(t) = P + t \vec d \quad ( 0 \le t \le \infty )$$

在描述线段时，使用一对点{$P_0$和$P_1$}，则线段方程是：

$$S(t) = P_0 + t \vec {(P_1 - P_0)} \quad (0 \le t \le 1)$$

平面的描述方式很多，最简单的是使用一般式 $ax+by+cz+d = 0$，向量 $\vec n = [a, b, c]$是平面的法向量。

1. 直线与平面相交

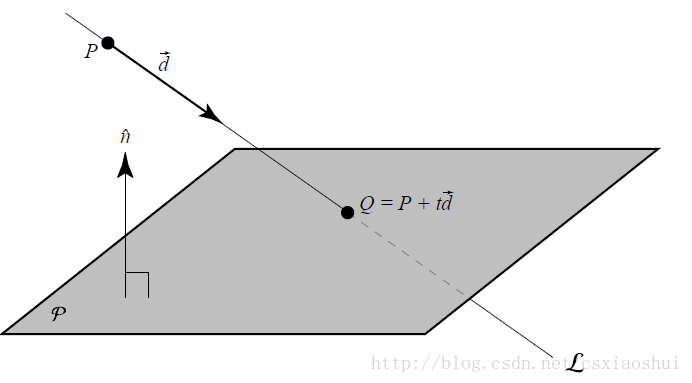
如上图所示，直线方程L是 $P + t \vec d$， 平面方程是 $ax+by+cz+d = 0$，假设二者有交点（交于点Q），那么直线上的Q点也一定满足平面方程，也就是：

$Q = P + t \vec d$ 满足 $ax+by+cz+D = 0$ （为区别直线的方向向量，平面方程的常数项写成D)，将Q点带入平面方程中，得到：

$$a (P_x + t d_x) + b(P_y + t d_y) + c(P_z+t d_z) + D = 0$$
$$t = \frac {-(D + aP_x + bP_y+cP_z)} {ad_x+bd_y+cd_z}$$

写成向量的形式是：

$$t = \frac {-(D + \vec n \cdot P)} {\vec n \cdot \vec d}$$

针对这个表达式展开讨论：

1. 如果 $\vec n \cdot \vec d = 0$ 那么说明直线平行于平面或者直线位于平面之内。怎么判断直线是否位于平面之内呢？很简单，判断直线的另一个点P是否位于平面内即可，也就是把P点带入平面方程中，如果满足平面方程，那么直线位于平面内，不满足则二者平行。
2. 如果 $\vec n \cdot \vec d \ne 0$，那么直线和平面有唯一的交点，将t值带入到 $Q = P + t \vec d$可以求出二者的交点坐标。

总结如下：

1. $\vec n \cdot \vec d = 0$ 且 $aP_x+bP_y+cP_z+D=0$ 直线位于平面内
2. $\vec n \cdot \vec d = 0$ 且 $aP_x+bP_y+cP_z+D \ne 0$直线与平面平行
3. $\vec n \cdot \vec d \ne 0$ 直线与平面有唯一交点

在编码过程中由于浮点数的舍入误差，一般将结果与一个阈值$\epsilon$进行比较，通过比较快速判断直线与平面是否相交。

2. 射线与平面相交

射线的方程表达式与直线类似，但是射线稍有不同的是它表达式中的 P一定是射线的端点，如果P是射线的端点，那么计算的过程与直线中的结论完全一样，只不过需要在判断相交的时候t的取值，如果取值范围 $t \ge 0$，那么就可以带入到射线方程中求出交点Q，否则（也就是$t \lt 0$）二者没有交点。

总结如下：

1. $\vec n \cdot \vec d = 0$ 且 $aP_x+bP_y+cP_z+D= 0$ 直线位于平面内
2. $\vec n \cdot \vec d = 0$ 且 $aP_x+bP_y+cP_z+D \ne 0$ 直线与平面平行
3. $\vec n \cdot \vec d \ne 0$ 且 $t \ge 0$ 射线与平面有唯一交点
4. $\vec n \cdot \vec d \ne 0$ 且 $t \lt 0$ 射线与平面没有交点

3. 线段与平面相交

线段的计算过程同样与射线类似，可以通过直线方程

$$S(t) = P_0 + t \vec {(P_1 - P_0)} \quad (0 \le t \le 1)$$

来计算，需要注意的是线段的方向向量 $\vec d$，必须是 $P_1 - P_0$，这样t的取值范围就是在[0,1]区间，如果t的取值范围不是[0,1]，那么线段与平面无交点。

总结如下：

1. 直线方程的方向向量必须是$P_1 - P_0$ （直线和射线只要方向相同即可，甚至可以单位化方向向量，但是线段必须是$P_1 - P_0$）
2. $\vec n \cdot \vec d = 0$ 且 $aP_x+bP_y+cP_z+D= 0$ 直线位于平面
3. $\vec n \cdot \vec d = 0$ 且 $aP_x+bP_y+cP_z+D \ne 0$ 直线与平面平行
4. $\vec n \cdot \vec d \ne 0$ 且 $t \in [0, 1]$ 射线与平面有唯一交点
5. $\vec n \cdot \vec d \ne 0$ 且 $t \notin [0, 1]$ 射线与平面没有交点

4. 算法实现

使用OpenSceneGraph实现线段和平面的相交判断的代码如下：

/* 
*  线段和平面的相交关系判断:返回值是0表示没有交点，返回值是1表示二者有唯一交点，返回值是2表示线段位于平面内
*
*/

int intersectSegmentPlane(const osg::Plane& plane, const osg::LineSegment& lineSegment, osg::Vec3d& intersection)
{
    double epsilon = 1e-6;

    osg::Vec3d planeNorm = plane.getNormal();
    osg::Vec3d segmentDirection = lineSegment.end() - lineSegment.start();

    double dotPlaneNormSegDir = planeNorm * segmentDirection;

    osg::Vec4d planeParam = plane.asVec4();

    double lineInPlane = planeParam.x() * lineSegment.start().x() + planeParam.y() * lineSegment.start().y() +
        planeParam.z() * planeParam.z() + planeParam.w();

    if (fabs(dotPlaneNormSegDir) < epsilon)
    {
        //如果直线端点满足平面方程，那么直线在平面内
        if (fabs(lineInPlane) < epsilon)
        {
            return 2;
        }
        else
        {
            return 0;
        }
    }

    double planeNormDotP = -(planeParam.w() + planeNorm * lineSegment.start());
    double t = planeNormDotP / dotPlaneNormSegDir;

    if (t < 0 || t > 1)
        return 0;

    intersection = lineSegment.start() + segmentDirection*t;

    return 1;
}

5. 参考文献

1. Line and Segment Intersections
2. [书籍：Geometric Tools for Computer Graphics]