floyd算法代码
弗洛伊德·沃霍尔 (Floyd Warshall)
The Floyd Warshall algorithm, itis the algorithm in which there is the use of different characterization of structure for a shortest path that we used in the matrix multiplication which is based on all pair algorithms. The algorithm considers the intermediate vertices of the shortest path, where an intermediate vertex of a simple path p =< v1, v2, ..., VL> is any vertex of p other than v1 or VL, that is, a vertex in the set {v2, v3,..., vl-1}.
Floyd Warshall算法是一种算法,其中我们在基于所有对算法的矩阵乘法中使用了最短路径的不同结构表征。 该算法考虑最短路径的中间顶点,其中简单路径p = <v1,v2,...,VL>的中间顶点是除v1或VL以外的p的任何顶点,即设置{v2,v3,...,vl-1} 。
The Floyd Warshall algorithm is based on the following observation. Suppose the vertices of the G be V = {1, 2,..., n}, and assume a subset {1, 2, ..., k} of the vertices for some k. For any pair of vertices i, j £ v consider that all paths from i to j which have their intermediate vertices all drawn from {1, 2,..., k}, and now let p be the minimum weight path from among them. The relationship between path p and shortest paths from i to j with all intermediate vertices in a set {1, 2,..., k-1} is exploited by the Floyd Warshall algorithm.
Floyd Warshall算法基于以下观察。 假设G的顶点是V = {1,2,...,N},并且假设顶点对某个k的子集{1,2,...,K}。 对于任何一对顶点i , j£v都认为从i到j的所有路径的中间顶点都取自{1,2,...,k} ,现在令p是其中的最小权重路径。 Floyd Warshall算法利用路径p和从i到j的最短路径之间的所有中间顶点在集合{1,2,...,k-1}中的关系。
Let the weight of a shortest path from vertex i to the vertex j with all intermediate vertices in the set {1, 2, ..., k} be d (ij) ^ (k), when k = 0, a path from vertex i to vertex j with no intermediate vertex numbered higher than 0 has no intermediate vertices at all. It has at most one edge, hence (ij) ^ (0) = w (ij), A recursive definition is given by
设从顶点i到顶点j且集合{1,2,...,k}中所有中间顶点的最短路径的权重为d(ij)^(k) ,当k = 0时 ,从从顶点i到顶点j ,没有中间顶点的编号大于0,根本没有中间顶点。 它最多具有一个边,因此(ij)^(0)= w(ij) ,递归定义为
d (ij) ^ (k) ={ w (ij) if k = 0
{Min (d (ij) ^ (k-1), d (ik) ^ (k-1) + d (kj) ^ (k-1) if k >= 1
Floyd Warshall算法 (Floyd Warshall Algorithm)
1. n = rows [W]
2. D ^ (0) = W
3. For k = 1 to n
4. Do for I = 1 to n
5. Do for j = 1 to n
6. d (ij) ^ (k) = min (d(ij) ^ (k-1), d (ik) ^ (k-1) + d(kj) ^ (k-1))
7. return D ^ (n)
The running time of the Floyd Warshall algorithm is determined by the triply nested for loop of line 3 to 6. Each execution of the line 6 takes O (1) time. Thus the algorithm runs in O (n ^ 3) time.
Floyd Warshall算法的运行时间由第3行到第6行的循环的三重嵌套确定。第6行的每次执行花费O(1)时间。 因此,该算法运行时间为O(n ^ 3)。
In the Floyd Warshall algorithm, there are many ways for the constructing the shortest paths. One way is to compute the matrix D of the shortest path weights and then construct the predecessor matrix π from the matrix D. This method can be implemented to run in O (n ^ 3) time.
在Floyd Warshall算法中 ,有许多方法可以构造最短路径。 一种方法是计算最短路径权重的矩阵D,然后从矩阵D构造先前的矩阵π。可以将该方法实现为在O(n ^ 3)时间内运行。
Example:
例:
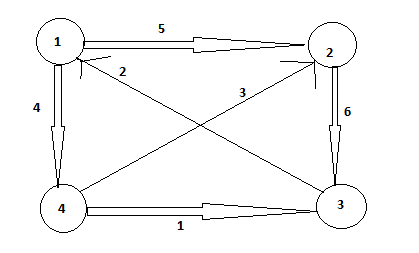
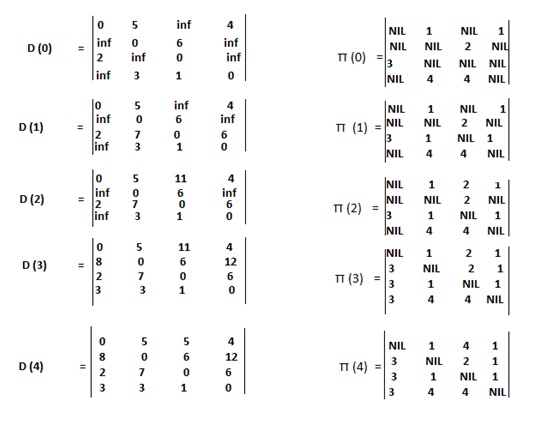
The sequence of matrices D ^ (k) and π ^ k (k computed by the Floyd Warshall algorithm) for given graph is computed as follows:
矩阵d ^(k)和π^ K(K 内由Floyd-Warshall算法计算的)对于给定的图形的序列被计算为如下:
References:
参考文献:
翻译自: https://www.includehelp.com/algorithms/floyd-warshall-algorithm-with-its-pseudo-code.aspx
floyd算法代码























 1171
1171

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








