前面在"C++均匀分布U(0,1)的随机数中”讲了如何在C++中生成均匀分布随机数,同时也提到了均匀分布的是其他随机数的生成基础,这里就来看看均匀分布在其他随机数生成中的重要作用吧,这里使用逆分布函数方法来说明:
我们知道,关于随机数的生成,许多编程语言都有对应的库支持(如:“用C++ TR1生成随机数"中提到的C++对几种常用的随机数的支持),同时matlab中对随机数的支持更是丰富,接近完备了,但是总会有那么个问题:随机数那么多,怎么可能有一个软件面面俱到。
这里,很重要的一点是:随机数种类其实是无穷无尽的,因为,随便一个函数,只要满足分布函数的几条公理就可以对应一种随机数,例如:我们知道F(x)=x;0<x<1是均匀分布的分布函数,密度函数为:f(x)=F'(x)=1;0<x<1;而F(X)=x^2;0<x<1也对应一种随机数,密度函数为f(x)=2x;0<x<1;只是因为他不如均匀分布那么常用,我们没有给它取个名字而已,但是并不代表他就没用了,现实世界那么多情况,不可能只用几种有有名字的分布就能完美描述的,所以这里想说的是,随机数并不是只有几种,只是有的你不知道他的名字而已,只要函数满足分布函数的公理体系那么他就对应一种随机数。
鉴于以上原因,这里要从根本上解决问题的话,就知道一种比较通用随机数生成算法,那么当没有软件后编程语言没有相关的库的时候,可以自己解决。而逆分布函数法是这样的算法中比较基础的算法:
先说明一下符号:U(0,1)-均匀分布,”~“表示服从xxx分布,F(x),为需要生成的随机数的分布函数,invF(x)表示逆分布函数,那么算法步骤如下:
step 1: 产生 u~U(0,1)
step 2:计算X=invF(u)
那么X就是服从分布函数为F(x)的随机数,一个简单的证明:
证明: P(X<y)=P(invF(u)<y)=P(u<F(y))=F(y); 证毕。
你会感觉好简单啊,对是很简,下面就给出两个例子,一个是常用的指数分布,另一个是不太用的双指数分布(Double Exponential):
首先,指数分布的分布函数:
F(x)=1-exp(-lamda*x);x>0( lamda 为参数)
因此逆分布函数:
invF(x)=-(1/lamda)*ln(1-x);0<x<1
所以随机数数产生过程:
step 1:产生u~U(0,1)
step 2: 计算X=-ln(1-u)
得到随机数
接着就是,双指数分布的了,可能大家跟我的反应一样,这是个什么分布啊。没听说过啊,其实我也是这几天做高等数理统计的作业时遇到的,这也是我这篇博客形成的最初原因。
下面贴个图你就明白了:
密度函数:
分布函数:
逆分布函数:
其中啊a,b 为参数,好了这就可以产生Double Exponentia的随机数了。
最后提到一点的是,逆分布函数法,还可以用于生成离散型的随机数,只是此时的分布函数数分段的,逆分布的函数也是分段的所以这里需要用一个数组来存储各个段,所以实现起来会有点点复杂,不过对于有的离散型分布的的话,其他的方式会更好,看情况来吧!
程序我就不放上来了,除了一些必要的框框之外,就那么几行代码,只是写的石后均匀分布的随机数产生最好使用标准库提供的,虽然我们都可以自己写一个,但是,为了保证其至少是可用的,那么你必须做一下假设检验之类的检验,检验你的算法不会被显著的拒绝,注意证明他是不可能的(至少据我所知是这样的),但是要用C++做假设检验会有点麻烦,所以推荐使用标准库。











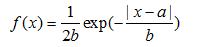
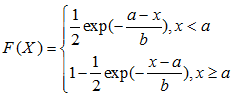















 705
705

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








