HDU杭电--机器学习实验报告（七）

• 实验目的

• 1、理解无监督学习中PCA、NMF降维算法原理:

• 2、掌握Sklearn实现基于PCA、NMF方法及应用

• 实验内容与要求

主成分分析(PrincipalComponentAnalysis，PCA)是最常用的一种降维方法，通常用于高维数据集的探索与可视化，还可以用作数据压缩和预处理等。PCA可以把具有相关性的高维变量合成为线性无关的低维变量称为主成分。主成分能够尽可能保留原始数据的信息。

PCA的作用主要有两个方面：一是降维，将高维数据集转化为低维数据集，以便于可视化和分析；二是提取特征，通过将数据投影到主要方差所在的子空间，PCA能够提取出数据集中的关键特征，从而更好地了解数据的分布和结构。

原理:矩阵的主成分就是其协方差矩阵对应的特征向量，按照对应的特征值大小进行排序，最大的特征值就是第一主成分，其次是第二主成分，以此类推。

【sklearn中主成分分析】

在sklearn库中，可以使用sklearn.decomposition.PCA加载PCA进行降维，主要参数有: ncomponents:指定主成分的个数，即降维后数据的维度·svd solver:设置特征值分解的方法，默认为'auto’,其他可选有'ful','arpack','randomized'.

【PCA实现高维数据可视化】

目标:已知鸢尾花数据是4维的共三类样本。使用PCA实现对鸢尾花数据进行降维，实现在二维平面上的可视化。

• 实验程序与结果

import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
import pandas as pd
import argparse
import matplotlib.font_manager as fm
def main(n_components):
    # 获取鸢尾花数据集
    iris = load_iris()
    Y = iris.target  # 数据集标签 ['setosa', 'versicolor', 'virginica']
    X = iris.data  # 数据集特征 四维，花瓣的长度、宽度，花萼的长度、宽度
    # 数据标准化
    X = StandardScaler().fit_transform(X)

    # 调用PCA进行降维
    pca = PCA(n_components=n_components)  # 实例化
    X_dr = pca.fit_transform(X)  # 拟合并降维
    # 输出各主成分的方差解释比例
    explained_variance = pca.explained_variance_ratio_
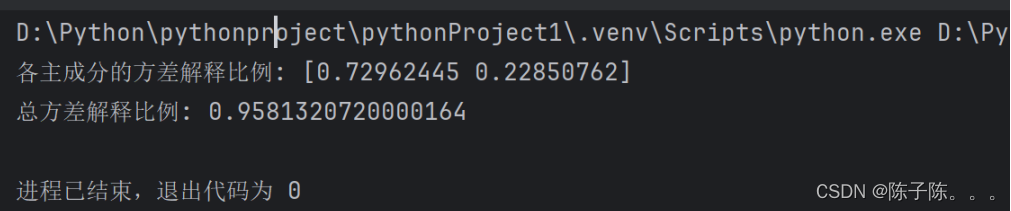
    print(f"各主成分的方差解释比例: {explained_variance}")
    print(f"总方差解释比例: {explained_variance.sum()}")
    # 设置字体
    font_path = 'C:\\Windows\\Fonts\\msyh.ttc'
    my_font = fm.FontProperties(fname=font_path)

    # 可视化方差解释比例
    plt.figure()
    plt.bar(range(1, n_components+1), explained_variance, alpha=0.7, align='center')
    plt.ylabel('方差比例', fontproperties=my_font)
    plt.xlabel('主成分', fontproperties=my_font)
    plt.title('各主成分的方差解释比例', fontproperties=my_font)
    plt.show()
    # 对三种鸢尾花分别绘图
    if n_components == 2:
        colors = ['green', 'red', 'blue']
        plt.figure()
        for i in [0, 1, 2]:
            plt.scatter(X_dr[Y == i, 0],  # x轴
                        X_dr[Y == i, 1],  # y轴
                        alpha=0.7,  # 图表的填充不透明度(0到1之间)
                        c=colors[i],  # 颜色
                        label=iris.target_names[i]  # 标签
                        )
        plt.legend(prop=my_font)  # 显示图例
        plt.title('鸢尾花数据集的PCA', fontproperties=my_font)  # 设置标题
        plt.xlabel('主成分1', fontproperties=my_font)
        plt.ylabel('主成分2', fontproperties=my_font)
        plt.show()
    else:
        print(f"无法绘制{n_components}个主成分的散点图。只有2个主成分可以绘制。")

if __name__ == "__main__":
    parser = argparse.ArgumentParser(description="鸢尾花数据集的PCA")
    parser.add_argument('--components', type=int, default=2, help='PCA的主成分数量')
    args = parser.parse_args()
    main(args.components)

四、实验结果分析

PCA是一种通过线性变换将原始数据集转换为新的坐标系，使得变换后的数据在新的坐标系下具有以下特点：第一，新坐标系中的第一个坐标（也称为第一主成分）尽可能地反映了数据集中的最大方差；第二，新坐标系中的每个坐标（即主成分）都是正交的，即数据在每个主成分上的波动互不影响。

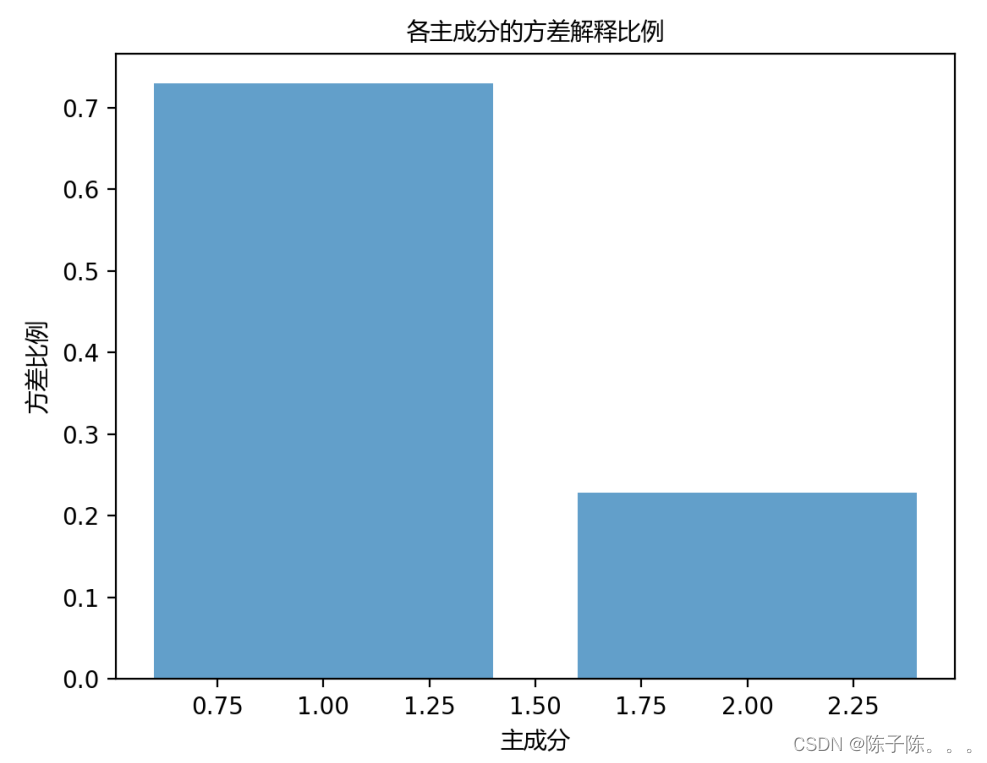
图一是各主成分的方差解释比例，前两个主成分的方差解释比例分别为0.7296和0.2285，总方差解释比例为0.9581。这意味着前两个主成分能够解释原始数据中95.81%的方差信息，即PCA降维后的数据保留了大部分原始数据的信息。

第一个主成分（PC1）解释了72.96%的方差，说明其捕获了数据中大部分的变异信息。第二个主成分（PC2）解释了22.85%的方差，进一步补充了数据中次要的变异信息。

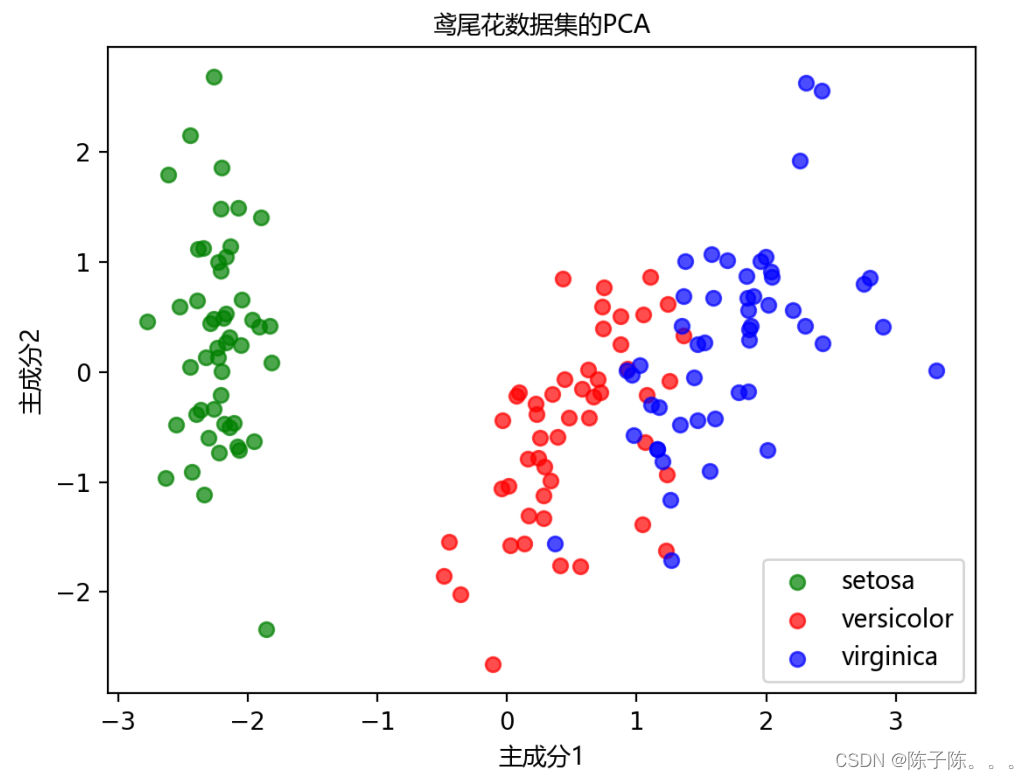
图二是鸢尾花数据集的CPA，展示了在两个主成分空间中，三种鸢尾花的分布情况。绿色点在主成分空间中形成一个清晰且独立的簇，与其他两种鸢尾花明显分开，红色和蓝色点在主成分空间中有一些重叠，但大多数数据点仍然可以区分。Setosa与Versicolor和Virginica之间的明显分离，表明这三类鸢尾花在前两个主成分空间中有显著区别，而Versicolor和Virginica之间的重叠表明它们在特征空间中有一些相似之处，仍能通过PCA进行一定程度的区分。

五、实验问题解答与体会

主成分分析（PCA）是一种广泛应用于高维数据的降维方法。 通过将数据投影到由数据集的主成分所构成的子空间，PCA能够简化数据的维度，同时保持数据集中的最大方差，此次实验让我更深刻地理解了PCA降维算法原理及其应用。

当然，也让我明白了，在编写代码之前，务必仔细检查文件路径和文件名，确保它们是正确的。在处理数据时，要格外注意数据的质量和完整性，以避免在后续的分析和建模过程中出现问题。对于模型训练效果不佳的情况，需要耐心和细心地调整模型参数、优化数据预处理步骤，并且不断尝试不同的方法，直到找到合适的解决方案。通过不断学习和尝试代码算法，才会得到实用的经验和教训。所以，在以后的工作中，我需要要保持持续学习的态度，不断改进和优化模型，提高工作效率和质量。