AI绘画教程基础篇----1秒都不浪费！采样方法和步数的最优选择

省流结论：

1、EULER \EULER-a, DPM2\DPM2a DPM++系列,DDIM都是值得保留的。

2、采样步数在20-30之间，DPM++采样在20以内已经能够得到较好的结果，是比较高效率的采样。

概念：

AI绘图遵循采样步数-发散-收敛的过程，一定步数之后，结果趋于收敛 - 也就是说，随着-samples（步长）值的增加，图像看起来越来越相似，直到出现图像不再变化的点。

对于新手来说，常用的采样就有那么多：

这里面少了HEUN和LMS，这两个我并不常用。原因我放在后面。

下面我们直接上对比结果图：

在上面的结果对比种，你觉得那种方法是最好的？

可以看到，EULER\HEUN\DPM2\DDIM\LMS\PLMS这些的风格化是很相似的。

其中，HEUN、EULER、DPM_2、DDIM在大概10步左右已经产生了稳定结果。

因此，我们先行淘汰了较老的LMS\PLMS采样法。

同时。EULER-A,DPM_2得以保留，这两种方法能够带来不太一样的结果。而且EULER-A在11月之前一直还是速度最快的采样方法。

剩下的HEUN、EULER、DPM_2、DDIM四种方法之中，HEUN的采样步数比较少，但速度比较慢。 所以，我也把它淘汰了。

到了11月，中国的几名学者发布了DPM++系列的采样方法。这两种采样的效率提升很快。效果可以看下图最下面两行：

基本上，DPM++系列在16步就完成了收敛。如果选20步以内的采样，DPM++2M的方案是目前速度最快的。

一个参考数据是：

在我的3080/2080TI上，512*512，DPM++2M，20步的采样，能跑到2秒1图。

在我的3060上，512*512，DPM++2M，20步的采样，能跑到4秒1图。

这种速度，都是以前不敢想的，算是采样方法改进带来的效率提升了。

写在最后

感兴趣的小伙伴，赠送全套AIGC学习资料，包含AI绘画、AI人工智能等前沿科技教程和软件工具，具体看这里。

AIGC技术的未来发展前景广阔，随着人工智能技术的不断发展，AIGC技术也将不断提高。未来，AIGC技术将在游戏和计算领域得到更广泛的应用，使游戏和计算系统具有更高效、更智能、更灵活的特性。同时，AIGC技术也将与人工智能技术紧密结合，在更多的领域得到广泛应用，对程序员来说影响至关重要。未来，AIGC技术将继续得到提高，同时也将与人工智能技术紧密结合，在更多的领域得到广泛应用。
 

一、AIGC所有方向的学习路线

AIGC所有方向的技术点做的整理，形成各个领域的知识点汇总，它的用处就在于，你可以按照下面的知识点去找对应的学习资源，保证自己学得较为全面。

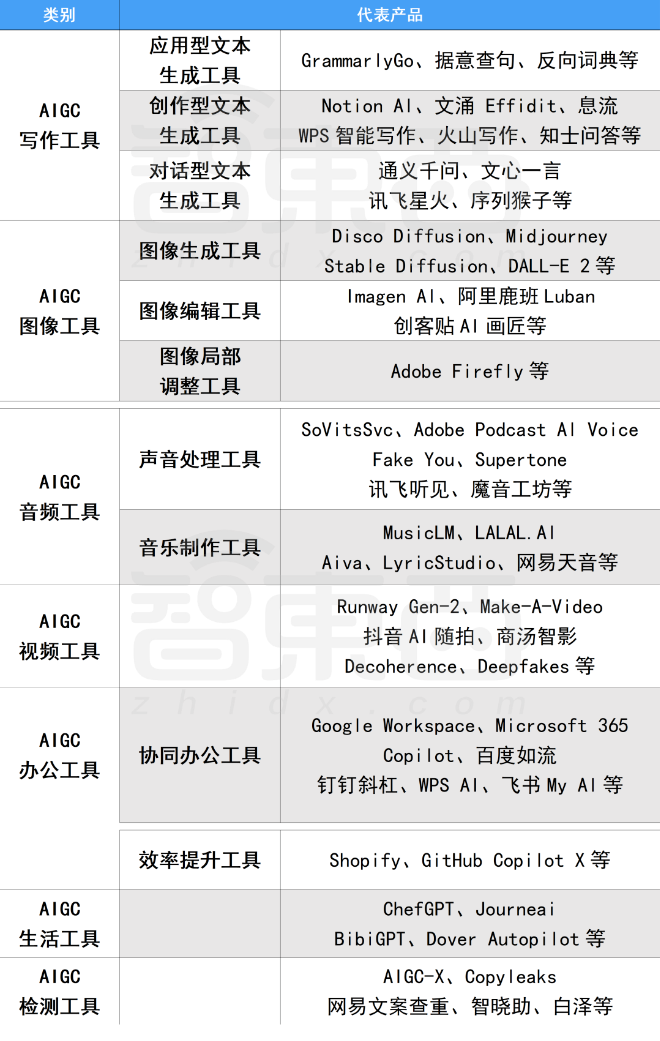
二、AIGC必备工具

工具都帮大家整理好了，安装就可直接上手！

三、最新AIGC学习笔记

当我学到一定基础，有自己的理解能力的时候，会去阅读一些前辈整理的书籍或者手写的笔记资料，这些笔记详细记载了他们对一些技术点的理解，这些理解是比较独到，可以学到不一样的思路。

四、AIGC视频教程合集

观看全面零基础学习视频，看视频学习是最快捷也是最有效果的方式，跟着视频中老师的思路，从基础到深入，还是很容易入门的。

五、实战案例

纸上得来终觉浅，要学会跟着视频一起敲，要动手实操，才能将自己的所学运用到实际当中去，这时候可以搞点实战案例来学习。

若有侵权，请联系删除