【学习笔记】计算机时代的统计推断（Bradley Efron and Trevor Hastie 著）

最新推荐文章于 2022-03-03 16:43:45 发布

囚生CY

最新推荐文章于 2022-03-03 16:43:45 发布

阅读量1.3w

点赞数 10

分类专栏：学习笔记文章标签：统计学机器学习

本文链接：https://blog.csdn.net/cy19980216/article/details/112004078

版权

学习笔记专栏收录该内容

13 篇文章

订阅专栏

序言

英文版教材免费下载地址: CASI

笔者本来是打算写来作为期末复习使用的, 但是发现写着写着变成了翻译教材, 实在是太草了; 本来以为提前一个星期动笔一定可以趁复习时顺手做完这本教材的摘要, 现在看来怕是要来不及了[Facepalm]…

笔者认为本书对于深究机器学习领域中的统计理论知识非常重要, 如果以后想要在机器学习方向做深入研究的话, 此书能够大大开拓使用机器学习方法的思路, 尤其是后半部分的章节与机器学习密切相关, 对诸如交叉验证, 自助法, 深度学习中的参数评估做了详细的理论分析, 非常值得好好学习一遍, 可惜课上讲到第12章就结束了;

本文长期更新, 笔者对该教材非常感兴趣, 眼下迫于期末复习无法详细做完所有笔记, 目前只做完了前三节的内容, 后续重点会就机器学习相关章节做一些笔记, 其他章节可能就以总结重点的形式一笔带过, 因为前面的几个章节主要还是基础的统计知识, 大部分可以在教科书上找到, 总之不能像前三节一样费时间写了, 实在是来不及了…

PART 1 经典统计推断 Classic Statistical Inference

1 算法与推断 Algorithms and Inference

统计科学是从经验中进行知识学习的学科, 尤其是那种每次都只有有少量积累的经验, 如:

(1) 新研发的实验药品成功与否;
(2) 小行星通往地球路径的不确定测算;

样本均值估计 $\bar x=\sum_{i=1}^n\frac{x_i}{n}\tag{1.1}$ 的标准误差估计值为: $\widehat{\rm se}=\left[\sum_{i=1}^n\frac{(x_i-\bar x)^2}{n(n-1)}\right]^{\frac{1}{2}}\tag{1.2}$

$(1.1)$ 中均值计算属于一种推断算法;
$(1.2)$ 中的标准误差值可以表示该推断算法的精确性, 标准误差越小, 精确度越高;
- 标准误差: 指在给定样本 $\bm{X}=\{x_1,x_2,...,x_n\}$ 的条件下, 样本统计量 $T(\bm{X})$ 的标准差;
- 此处 $T(\bm{X})=\bar x$ , 则标准误差估计值 $\widehat{\rm se}$ 计算公式为: $\left[\sum_{i=1}^n\frac{1}{n^2}{\rm Var(x_i)}\right]^{\frac{1}{2}}=\left[n\cdot\frac{1}{n^2}\cdot\frac{(x_i-\bar x)^2}{(n-1)}\right]^{\frac{1}{2}}=\left[\sum_{i=1}^n\frac{(x_i-\bar x)^2}{n(n-1)}\right]^{\frac{1}{2}}$
结论: 提供统计推断的一组样本数据, 同样可以用来评估该推断结果的精确性;

1.1 一个回归示例 A Regression Example

本节给出一个肾功能随年龄变化的回归分析模型: $y={\hat\beta}_0+{\hat \beta}_1x\tag{1.3}$ 并使用最小二乘法优化目标函数 $\sum_{i=1}^n(y_i-{\hat\beta}_0-{\hat \beta}_1x_i)^2\tag{1.4}$

Figure 1.1中给出的是样本散点图以及使用最小二乘法得到的线性回归拟合直线(绿线);
- 注意到拟合绿线上的垂直黑线表示该点估计值正负两倍的标准误差;
- 具体标准误差值详见Table 1.1;
  - 每个拟合预测点 $x = 20, 30, 40, 50, 60, 70, 80$ 处的标准误差即为 ${\hat\beta}_0+{\hat \beta}_1x$ 的标准误差; 应该是通过 $[{\rm se}({\hat\beta}_0)^2 + x^2{\rm se}({\hat\beta}_1)^2]^{\frac{1}{2}}$ 的方法计算得到的;
  - 最小二乘法中参数 ${\hat\beta}_0$ 与 ${\hat \beta}_1$ 的标准误差分别为: ${\rm se}({\hat\beta}_0)={\hat\sigma}^2\left(\frac{1}{n}+\frac{\bar x^2}{\rm SXX}\right)\\{\rm se}({\hat\beta}_1)=\frac{{\hat\sigma}^2}{\rm SXX}$ 其中: ${\hat\sigma}^2=\frac{1}{n-2}\sum_{i=1}^n(y_i-{\hat\beta}_0-{\hat \beta}_1x_i)^2\\{\rm SXX}=\sum_{i=1}^n(x_i-\bar x)^2=\sum_{i=1}^nx_i(x_i-\bar x)$
    - ${\hat\sigma}^2$ 是最小二乘方差的无偏估计;

Figure 1.2与Figure 1.3中分别是肾功能案例的局部加权回归(Lowess)与bootstrap采样下的Lowess拟合结果;

关于局部加权回归的具体算法可以参考【算法】局部加权回归（Lowess） ; 大致思路是: 以一个点 $x$ 为中心, 向前后截取一段长度为 $\rm frac$ 的数据, 对于该段数据用权值函数 $w$ 做一个加权的线性回归, 记 $(x,\hat y)$ 为该回归线的中心值, 其中 $\hat y$ 为拟合后曲线对应值, 对于所有的 $n$ 个数据点可以作出 $n$ 条加权回归线, 每条回归线的中心值的连线则为这段数据的Lowess回归拟合曲线;
Figure 1.2与Figure 1.3中的 $\rm frac$ 即为 $\frac{1}{3}$
注意到Lowess回归很难使用公式来计算其标准误差, 但是可以使用bootstrap多次重采样来近似估计其标准误差, 这就是Figure 1.3所做的事情, 这里作者做了250次重采样, Figure 1.3显示得是前25次重采样得Lowess回归拟合曲线;
Table 1.1中有Lowess回归的预测值及bootstrap重采样下的标准误差估计值, 可以看到Lowess回归是以较大的标准误差换来了平滑的预测结果;

1.2 假设检验 Hypothesis Testing

本节主要介绍假设检验的方法论进展;

本节给出的是一个两种白血病( $\rm ALL$ 与 $\rm AML$ )患者的样本案例; 72个白血病患者, 45个是ALL, 27个AML, Figure 1.4中给出了这些患者136号基因的活跃度的频数直方图:

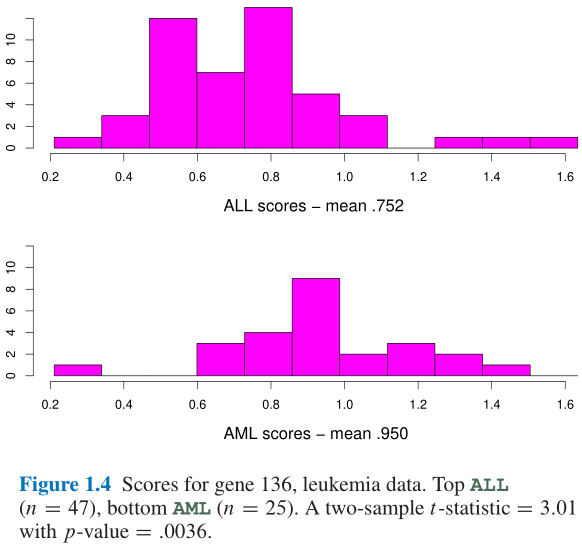
$\overline{\rm ALL}=0.752\quad\overline{\rm AML}=0.950\tag{1.5}$

似乎 $\rm AML$ 的136号基因的活跃度要更高一些; 但是这是否是统计上的一个侥幸现象(a statistical fluke)? 这可以使用两样本的 $t$ 检验来回答: $t=\frac{\overline{\rm AML}-\overline{\rm ALL}}{\widehat {\rm sd}}\tag{1.6}$
- 其中 $\widehat {\rm sd}$ 是Formula 1.6分子的标准差;
- 计算结果 $t = 3.01$ 是一个标准零分布(null distribution)中的值, 本例中是自由度为70的 $t$ 分布, 即可得出这是一个双侧显著水平为0.0036的检验, 置信水平是非常高的;

但是Figure 1.5中又给出了一个7182个样本量的相同案例统计结果:

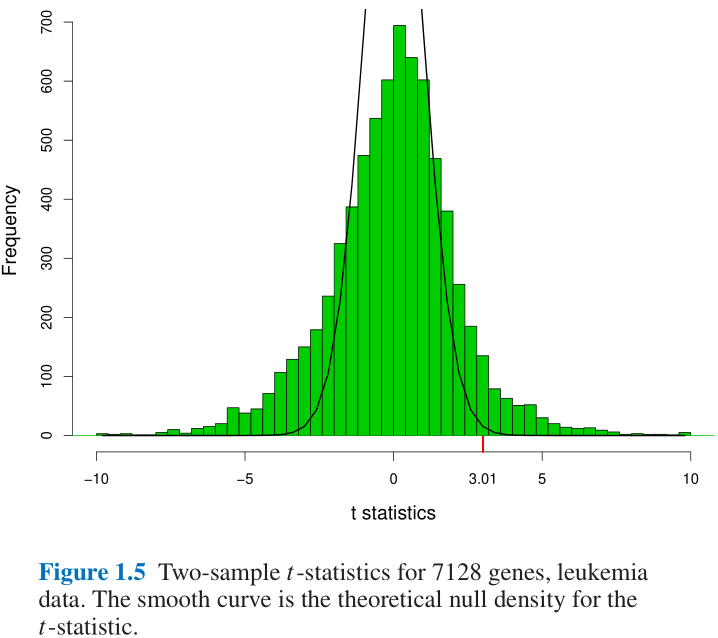
注意到自由度为70的 $t$ 分布近似为正态分布, 使用 $3\sigma$ 的估计结果可以知道大于 $3.01$ 的样本数应当占比约为 $1\%$ 即71个左右的异常值样本;
但是Figure 1.5中可以看到实际上会有400多个异常值样本;
作者将其归因于样本并非独立同分布, 使得零分布(自由度为70的 $t$ 分布)的假设是不成立的;
因此这里有提出很多后续需要研究的概念:
- Chapter 15中的错误发现率(false-discovery rate);
- 频率学派与与贝叶斯学派的结合;
- Chapter 6中的经验贝叶斯;
- Chapter 20中的同时置信区间: 当需要做 $m$ 个假设检验时, 想要将显著水平控制在 $\alpha$ 一下, 则要求单个假设检验的显著水平要在 $\frac{\alpha}{m}$ 以下;

2 频率推断 Frequentist Inference

梅尔博士的肾脏学实验:

检测211个肾脏病患者的 $\rm gfr$ 指标, 根据Formula 1.1与Formula 1.2计算得到的均值估计与标准误差估计为 $\bar x=54.25$ 与 $\widehat {\rm se}=0.95$ , 因此可以统计描述可以表达为: $54.25\pm0.95\tag{2.1}$ 其中 $±0.95 \pm0.95$ 表示对于估计量 $\bar x=54.25$ , 频率推断出的精确度; 这说明其实别太对 $54.25$ 的误差其实很大, 不仅小数位不可信, 连个位数 $4$ 的可信度也很低;

频率推断:

令 $\bm{X}=(X_1,X_2,...,X_n)$ 是 $n$ 个从概率分布 $F$ 中独立抽取出来的 $n$ 个样本: $F\rightarrow\bm{X}\tag{2.2}$ 这里的 $F$ 就是 $\rm gfr$ 值的未知分布, 而我们得到的观测样本 $\bm{X}=\bm{x}=(x_1,x_2,...,x_n)$ , 而频率推断希望从观测样本上推断出未知分布 $F$ 的一些性质;
假设参数 $\theta$ 是 $\bm{X}$ 的数学期望: $\theta=E_F(\bm{X})\tag{2.3}$
事实上频率推断中会不断采样 $\bm{X}$ , 得到观测样本 $\bm{x}$ , 从而获得估计值 $\hat\theta=t(\bm{x})\tag{2.4}$ ,每次采样会得到一个不同的均值估计值 $\Theta$ , 则可以记随机变量 $\hat\Theta=t(\bm{X})\tag{2.5}$
定义 $\mu$ 为 $\hat\Theta=t(\bm{X})$ 的数学期望, 即: $\mu=E_F(\hat\Theta)\tag{2.6}$ 则参数 $\theta$ 的估计量 $\hat\theta$ 的偏差与方差分别为 ${\rm bias}=\mu-\theta\quad{\rm var}=E_F\left[(\hat\Theta-\mu)^2\right]\tag{2.7}$

2.1 频率主义的实际应用 Frequentism in Practice

频率主义的工作定义: the probabilistic properties of a procedure of interest are derived and then applied verbatim to the procedure’s output for the observed data.

简而言之就是从分布 $F$ 中计算出估计量 $\hat\Theta=t(\bm{X})$ 的性质, 即使 $F$ 是未知的;

应用举例:

(1) The plug-in principle:
- 用原模型分布产生的数据分布来估算模型本身的分布, 然后将预估出来的参数插入到原分布中以做出最优预测;
- 如可以将分布 $F$ 下的样本均值 $\bar X=\frac{\sum X_i}{n}$ 的标准误差与 ${\rm var}_F(X)$ 联系起来: ${\rm se}(\bar X)=\left[\frac{{\rm var}_F(X)}{n}\right]^{\frac{1}{2}}\tag{2.8}$ 我们只有观测到的样本数据 $\bm{x}=(x_1,x_2,...,x_n)$ , 于是只能进行估计: ${\widehat {\rm var}}_F=\sum\frac{(x_i-\bar x)^2}{n-1}\tag{2.9}$ 将Formula 2.9嵌入到Formula 2.8中就可以得到Formula 1.2中的估计值 $\widehat{\rm se}$ ;
- 拓展:
  - ① 如 $\theta=E(X)$ 的估计量为 $\frac{\sum_{i=1}^nX_i}{n}$ , 通过R-S Integral可以知道 $\theta=E(X^2)$ 的估计量为 $\frac{\sum_{i=1}^nX_i^2}{n}$
  - ② 关于 ${\rm var}(\bar X)$ 的估计值, 可以使用 ${\rm var}(\bar X)=\frac{\sigma^2}{n}=\frac{1}{n}\left\{\int x^2{\rm d}F(x)-\left[x{\rm d}F(x)\right]^2\right\}$ , 则可以得到: $\widehat {\rm var}(\bar X)=\frac{1}{n}\left\{\int x^2{\rm d}F_n(x)-\left[x{\rm d}F_n(x)\right]^2\right\}$
(2) Taylor-series approximations: 如果统计量 $\hat\theta=t(\bm{x})$ 比 $\bar x$ 复杂得多, 则可以回归到局部线性近似, 使用delta method来进行参数估计;
- 如 $KaTeX parse error: Undefined control sequence: \gat at position 1: \̲g̲a̲t̲\theta={\bar x}…$ 的导数为 $\frac{{\rm d}\hat\theta}{{\rm d}\bar x}=2\bar x$ , 视 $2\bar x$ 为一个常数则可以得到 ${\rm se}({\bar x}^2)=2\left|\bar x\right|\widehat{se}\tag{2.10}$ 其中 $\widehat{se}$ 在Formula 1.2中给出;
- 这个结论的一般情况是: ${\rm var}(g(\bar x))={\rm var}(g(\bar x)-g(\theta))=\left[g^\prime(\theta)\right]^2({\rm var}(\bar x-\theta))=\left[g^\prime(\theta)\right]^2({\rm var}(\bar x))$
(3) Parametric families and maximum likelihood theory: 这部分详见Chapter 4和Chapter 5中的最大似然估计的标准误差, 以及参数族分布, 会结合费雪理论, Taylor-series approximations以及The plug-in principle;
(4) Simulation and the bootstrap: 即仿真模拟与重采样方法;
(5) Pivotal statistics: 枢轴统计量;
- 枢轴统计量 $\theta=t(\bm{x})$ 是一个分布与未知分布 $F$ 无关的一个统计量; 以两样本 $t$ 检验为例: $\bm{x}_1=(x_{11},x_{12},...,x_{1n_1})\quad\bm{x}_2=(x_{21},x_{22},...,x_{2n_2})\tag{2.11}$ 其中 $X_{1i}\sim\mathcal{N}(\mu_1,\sigma^2)\quad i=1,2,...,n_1\tag{2.12}$ $X_{2i}\sim\mathcal{N}(\mu_2,\sigma^2)\quad i=1,2,...,n_2\tag{2.13}$ 我们希望检验零假设 $H_0:\mu_1=\mu_2\tag{2.14}$ 则显然的检验统计量 $\hat\theta={\bar x}_2-{\bar x}_1$ 的分布为 $\hat\theta\sim\mathcal{N}\left(0,\sigma^2\left(\frac{1}{n_1}+\frac{1}{n_2}\right)\right)\tag{2.15}$ 在零假设下我们希望将 $\sigma^2$ 的无偏估计量嵌入: ${\hat\sigma}^2=\frac{1}{n_1+n_2-2}\left[\sum_1^{n_1}(x_{1i}-{\bar x}_1)^2+\sum_1^{n_2}(x_{2i}-{\bar x}_2)^2\right]\tag{2.16}$
- 但是 $t$ 检验给出的方法更加优雅, 直接使用 $t$ 统计量: $t=\frac{{\bar x}_2-{\bar x}_1}{\widehat{sd}}\quad{\rm where}\space\widehat{\rm sd}={\hat\sigma}(\frac{1}{n_1}+\frac{1}{n_2})\tag{2.17}$ 此时在零假设 $H_0$ 下, $t$ 是一个枢轴量, 分布为自由度 $n_1+n_2-2$ 的 $t$ 分布, 而与参数 $\sigma$ 取值无关;
- 拓展: 一般方法为 $\frac{\sqrt{n}(\bar X-EX)}{\hat\sigma}\rightarrow\mathcal{N}(0,1)$ 其中 $\hat\sigma$ 使用The plug-in principle;

2.2 频率学派最优性 Frequentist Optimality

最大似然估计量的标准误差(或方差)一般都是最小的;
假设检验中设 $\alpha$ 为犯第一类错误的概率(舍真), $\beta$ 为犯第二类错误的概率(取假), 在样本量固定的情况下, 很难使得 $\alpha$ 和 $KaTeX parse error: Undefined control sequence: \ at position 1: \̲ ̲beta$ 同时下降, 因此一般最优性可以通过 $\alpha_c<\alpha\quad\beta_c<\beta\tag{2.23}$ 来取得, 即尽量使两种错误的概率在一个很小的范围内;

Neyman-Pearson Lemma(NP引理): 参考数理统计笔记：假设检验（II）N-P引理 ;
Figure 2.2中就给出了cut-off值在 $0.4$ 的情况下, 取得的最优假设检验结果;
频率推断的最优性一般是固定一个显著水平 $\alpha$ , 使得 $\beta$ 尽可能的小;

似然比检验的方法: https://zhuanlan.zhihu.com/p/104583619 ;

3 贝叶斯推断 Bayesian Inference

贝叶斯推断与频率推断即便不是对立的, 也至少是正交的两种概念, 它揭示了频率推断中令人担忧的缺陷, 却也让自身陷入过度使用的批判之中;
贝叶斯推断与频率推断的基础都是建立在某种概率密度分布族上: $\mathcal{F}=\{f_\mu(x);x\in\mathcal{X},\mu\in\Omega\}\tag{3.1}$ 其中 $\mathcal{X}$ 为样本空间, 未观测到的参数 $\mu$ 是在参数空间 $\Omega$ 中的一个点, 统计学家通过从 $f_\mu(x)$ 中观测 $x$ 来推断 $\mu$ 的数值;

最常见的正态分布: $f_\mu(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}(x-\mu)^2}\tag{3.2}$ 样本空间 $\mathcal{X}$ 与参数空间 $\Omega$ 都为 $\mathcal{R}^1$
另一种常见的泊松分布: $f_\mu(x)=\frac{\mu^x}{x!}e^{-\mu}\tag{3.3}$ 样本空间 $\mathcal{X}=\{0,1,2,...\}$ , 参数空间 $\Omega=(0,+\infty)$

贝叶斯推断与频率推断不同之处在于它除了概率分布族 $\mathcal{F}$ 依赖一个重要的假设, 即先验密度知识: $g(\mu)\tag{3.4}$ 其中 $g(\mu)$ 表示在观测 $x$ 之前就可以获得的与 $\mu$ 相关的分布信息; 如在Formula 3.2中我们至少可以知道 $\mu$ 是一个正数, 且过去的经验告诉我们 $\mu$ 没有出现过10以上的值, 那么就可以假设 $\mu$ 满足 ${1,2,3,4,5,6,7,8,9,10\}$ 上的均匀离散分布;
贝叶斯推断根据观测到的 $x$ 得到 $\mu$ 的后验分布 $g(\mu|x)$ ;

Bayes’ Rule(贝叶斯法则): $g(\mu|x)=\frac{g(\mu)f_\mu(x)}{f(x)}\quad\mu\in\Omega\tag{3.5}$ 其中 $f (x)$ 是 $x$ 的边际密度函数: $f(x)=\int_\Omega f_\mu(x)g(\mu){\rm d}\mu\tag{3.6}$
注意到Formula 3.5中当 $\mu$ 在 $\Omega$ 上变化时, $x$ 是一个固定的观测值, 于是可以将Formula 3.5改写为: $g(\mu|x)=c_xL_x(\mu)g(\mu)\tag{3.7}$ 其中 $L_x$ 是似然函数, 即 $f_\mu(x)$ 中 $x$ 固定, $\mu$ 变化, 一般来说 $L_x(\mu)=\prod_{i=1}^nf_\mu(x)$ ; $c_x$ 是用于调整概率密度函数求积为 $1$ 的系数;
推论: $\frac{g(\mu_1|x)}{g(\mu_2|x)}=\frac{g(\mu_1)f_{\mu_1}(x)}{g(\mu_2)f_{\mu_2}(x)}\tag{3.8}$ 即后验密度比等于先验密度比乘以似然比, 这是贝叶斯法则的精髓所在;

3.1 两个示例 Two Examples

第一个示例(Physicist’s Twins问题): 双胞胎分同卵(Identical)和异卵(Fraternal), 以及两个胎儿性别是否相同, 由此分为Figure 3.1的四种情况:
\

同卵必然性别相同, 异卵则性别是否相同的概率相等;
由此可以计算出在已知性别相同的条件下, 同卵和异卵的概率是相等的: $\frac{g({\rm Identical|Same})}{g({\rm Fraternal|Same})}=\frac{g({\rm Identical})}{g({\rm Fraternal})}\cdot\frac{f_{\rm Identical}({\rm Same})}{f_{\rm Fraternal}({\rm Same})}=\frac{1/3}{2/3}\cdot\frac{1}{1/2}=1\tag{3.9}$
但是在频率推断的情况下, 只看似然函数值的大小, 所以当观测到性别相同的情况时(即 $x = 0$ ):
- 若 $\mu=1$ , 即同卵双胞胎, 则 $f_\mu(x)=1$ ;
- 若 $\mu=1$ , 即异卵双胞胎, 则 $f_\mu(x)=\frac{1}{2}$ ;
- 那么就会偏向于推断是同卵双胞胎;
我们一般倾向于使用贝叶斯推断, 因为它使用了更多的(可靠的)先验信息;
当样本增多时, 先验分布就会越来越没有用处, 直到最终频率推断与贝叶斯推断趋于相同;

第二个示例(学生课程成绩): Table 3.1中展示了22个学生在两门课程上的成绩情况;

可以得到两门课程得分的相关系数值 $\hat\theta=0.498$ : $\hat\theta=\frac{\sum_{i=1}^{22}(m_i-\bar m)(v_i-\bar v)}{\left[\sum_{i=1}^{22}(m_i-\bar m)^2\sum_{i=1}^{22}(v_i-\bar v)^2\right]}\tag{3.10}$
因为只观测到了22个学生, 我们希望能够了解到所有学生的真实相关系数 $\theta$ 的后验贝叶斯测算的精确度;
如果假设 $(m, v)$ 的联合分布时二元正态分布, 则 $\hat\theta$ 的密度函数可以通过 $\theta$ 进行显式表达: $f_\theta(\hat\theta)=\frac{(n-2)(1-\theta^2)^{\frac{n-1}{2}}(1-{\hat\theta}^2)^{\frac{n-4}{2}}}{\pi}\int_0^\infty\frac{{\rm d}w}{(\cosh w-\theta\hat\theta)^{n-1}}\tag{3.11}$ 虽然这看似很复杂, 其实在计算机眼中这与初等函数没有太大区别;
如果假设 $\theta$ 是区间 $[- 1, 1]$ 上的均匀分布, 即 $g(\theta)=\frac{1}{2}\quad-1\le\theta\le1\tag{3.12}$ 即为flat prior, 那么Figure 3.2中给出了后验分布的情况, 此时最大似然估计取在密度最高处, 即 $0.498$ ;
- 当先验分布为均匀分布时, 后验分布的众数(密度最大点)即为最大似然估计量;
注意到Figure 3.2中还提到了另外两种先验:
- (1) Jeffreys prior: $g^{\rm Jeff}(\theta)=\frac{1}{1-\theta^2}\tag{3.13}$ 这源自于无信息先验理论; 这将在下一小节中提到, 虽然Formular 3.13其实并不符合密度函数的性质(求积为1, 这里求积为无穷), 但是当使用贝叶斯法则时仍然可以提供正确的结果;
- (2) Triangular prior: $g(\theta)=1-|\theta|\tag{3.14}$ 这是一种原始的压缩(shrinkage)先验, 使得后验分布趋向于零, 所以估计值会略小于 $0.498$ ;

这里好像作者相对于老版书删除了一些内容, 之后有空将课堂笔记补上:

贝叶斯的参数估计: 如最大后验估计(MAP), MMSE, MAE, 以及如何评估参数估计的精确度(MSE);
- 关于MSE的求法(在第四章的Note章节): ${\rm MSE}=E[(\hat\theta-\theta)^2]={\rm variance}+{\rm bias}^2\tag{4.47}$
  - 举个两个例子: 在二项分布 $x_i\sim B(n,\theta)$ 的情况下:
    - $\theta_{\rm MLE}=\bar x=\frac{\sum_{i=1}^nx_i}{n}$ , 这是无偏的, 所以直接计算方差即可: ${\rm MSE}(\hat\theta_{\rm MLE})={\rm var}\left(\frac{\sum_{i=1}^nx_i}{n}\right)=\frac{1}{n^2}{\rm var}(x_i)=\frac{1}{n}\theta(1-\theta)$
    - $\theta_{\rm B}=\frac{1+\sum_{i=1}^nx_i}{n+2}$ , 这是有偏的, 那么除了其自身的方差 $\frac{n\theta(1-\theta)}{(n+2)^2}$ 外, 还要加上偏差期望的平方: ${\rm bias}^2=E\left[\left(\frac{1+\sum_{i=1}^nx_i}{n+2}-\frac{\sum_{i=1}^nx_i}{n}\right)^2\right]=\left(\frac{n\theta+1}{n+2}-\theta\right)^2$
贝叶斯的参数置信区间;
贝叶斯的假设检验: 贝叶斯因子 $B(\bm{x})$ ;

3.2 无信息先验分布 Uninformative Prior Distributions

贝叶斯推断在给定先验分布时是非常好用的, 但是这个先验存在的假设条件太强, 使得未必存在先验知识可用, 因此提出无信息先验分布来解决这个问题; 所谓无信息先验即这样一个先验在应用到贝叶斯法则中后不会使得推断结果发生偏差;

原文: … implying that the use of such a prior in Bayes’ rule does not tacitly bias the resulting inference.

拉普拉斯认为均匀分布是无信息的(Laplace’s principle), 但是后来被维恩与费雪所推翻, 如参数 $\theta$ 一个均匀的先验分布将不再是均匀分布, 如果将参数调整为 $KaTeX parse error: Undefined control sequence: \gamme at position 1: \̲g̲a̲m̲m̲e̲=e^\theta$ , 则后验分布变为: $\Pr(\theta>0|\hat\theta)=\Pr(\gamma>1|\hat\theta)\tag{3.15}$ 将取决于 $\theta$ 与 $\gamma$ 是否被取自一个均匀的先验分布, 任何一个选择都不被认为是无信息的;
Jeffreys prior: Laplace’s principle的一种复杂版本;

费雪信息量: $\mathcal{I}_\mu=E_\mu\left[\left(\frac{\partial}{\partial\mu}\log f_\mu(x)\right)^2\right]\tag{3.16}$
Jeffreys prior定义为: $g^{\rm Jeff}(\mu)=\mathcal{I}_\mu^{\frac{1}{2}}\tag{3.17}$ 事实上 $\mathcal{I}$ 约等于最大似然估计 $\hat\mu$ 的方差 $\sigma_\mu^2$ 的倒数, 因此也可以表示为: $g^{\rm Jeff}(\mu)=\frac{1}{\sigma_\mu}\tag{3.18}$
这里提到Formula 3.11中哪个复杂的 $\hat\theta$ 估计值的标准差为: $\sigma_\theta=c(1-\theta^2)\tag{3.19}$ 事实上这里的系数 $c$ 对贝叶斯法则(Formular 3.5与Formular 3.6是没有影响的);、
Figure 3.2中的参数 $\theta$ 的贝叶斯置信区间为 $[0.093, 0.750]$ , 即 $\int_{0.093}^{0.750}g^{\rm Jeff}(\theta|\hat\theta){\rm d}\theta=0.95\tag{3.20}$

Chapter 4中会讨论多参数分布族, 比如观测到的10个独立样本均值是不相同的: $x_i\sim\mathcal{N}(\mu_i,1)\quad i=1,2,...,10\tag{3.21}$ 此时这10个问题的不仅每一个Jeffreys prior都是flat(这样就可以分开考虑每一个问题), 而且它们的联合Jeffreys prior也是flat: $g(\mu_1,\mu_2,...,\mu_{10})=\rm constant\tag{3.22}$ 显然计算机时代更多得是考虑Formular 3.21而非Formular 3.11这样的问题, 事实上无信息先验, 包括Jeffreys prior都是实际应用中非常流行的方法, 这使得贝叶斯学派与频率学派相互影响, 后者的目的是控制前者可能发生的推断偏差;

3.3 频率推断的缺陷 Flaws in Frequentist Inference

本节以一个案例分析来说明频率推断的缺陷;

电压计案例:

一个工程师测量12个管道的电压, 使用一个标准刻度的电压计: $x\sim\mathcal{N}(\mu,1)\tag{3.23}$ 其中 $x$ 是测量结果, $\mu$ 是真实地电压值, 测量结果从82~99波动, 均值 $\bar x=92$ , 工程师将均值作为 $\mu$ 的无偏估计值来报告;
第二天他发现电压计出了问题, 任何高于100伏的测量结果都只会显示为100伏, 于是频率学派的统计家告诉工程师 $\bar x=92$ 已经不再是无偏估计量了, 因为Formula 3.23不再能完全描述这组样本的概率分布, 事实上 $\bar x=92$ 已经偏小了;
显然我们直到电压计的问题并没有影响观测样本的准确性, 这使得工程师非常困扰, 此时贝叶斯学派的统计学家来解救工程师, 根据后验分布 $g(\mu|\bm{x})=\frac{g(\mu)f_\mu(\bm{x})}{f(\bm{x})}, 其中$ \bm{x} $为观测到的测量结果, 因此后验分布 = = 只与观测到样本$ \bm{x}$有关, 与其他没有观测到的数据是无关的==;
此时使用Jeffreys prior: $g(\mu)=\rm constant$ 仍然得到 $\mu$ 的估计值为 $\bar x=92$ , 与电压计是否出了故障是无关的;

Figure 3.3中给出了一种相对自然的案例: 一个正在进行的实验, 每个月会观测到一个独立的正态分布变量: $x_i\sim\mathcal{N}(\mu,1)\tag{3.24}$

此时我们给出一个假设检验: $H_0:\mu=0\space{\rm v.s.}\space H_1:\mu>0$ , 则Figure 3.3中绘制的散点是检验统计量: $Z_i=\frac{\sum_{j=1}^ix_j}{\sqrt{i}}\tag{3.25}$ 即一种基于直到第 $i$ 个月的数据计算出的 $z$ 值: $Z_i\sim\mathcal{N}(\sqrt{i}\mu,1)\tag{3.26}$
到第30个月时, 发现 $Z_{30}=1.66$ , 刚好超过了 $\mathcal{N}(0,1)$ 的 $95\%$ 分位点 $1.645$ , 于是观察员宣布可以以0.05的显著水平拒绝零假设;
然而不幸的是, 观察员没有遵守协定, 而想在第20个月时终止了这个昂贵的实验, 然后这是徒劳, 因为 $Z_20=0.79$ 并没有达到预定的显著水平, 于是仍然按照原计划实验进行到第30个月; 于是实验停止的条件变为了 $Z_20$ 或 $Z_30$ 的显著水平达标; 通过计算可以发现此时拒绝零假设(当零假设为真时)的概率是 $0.074$ 而非 $0.05$ ;
此时贝叶斯学派的统计学家就出来说, 全数据集 $\bm{x}=(x_1,x_2,...,x_{30})$ 的似然函数为: $L_{\bm{x}}(\mu)\prod_{i=1}^{30}e^{-\frac{1}{2}(x_i-\mu)^2}\tag{3.27}$ 将保持不变, 无论该实验是否提早停止了;

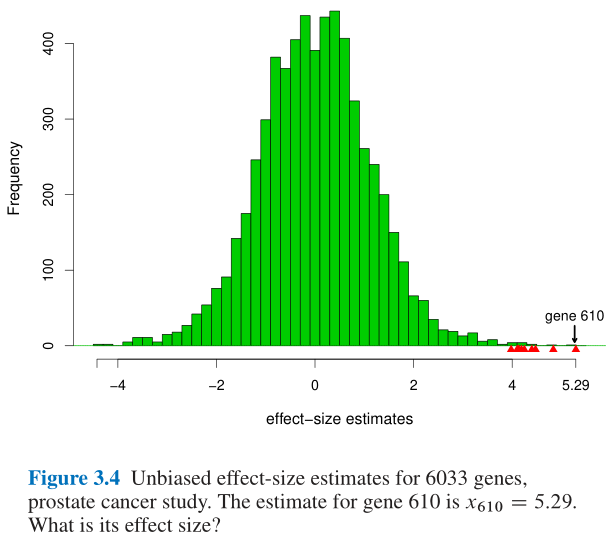
Figure 3.4又给出了另一个案例: 此处不再赘述, 详见教材P33;

3.4 贝叶斯学派与频率学派的比较清单 A Bayesian/Frequentist Comparison List

Figure 3.5: 贝叶斯推断是纵向进行的, 而频率推断是横向进行的;

贝叶斯学派: 固定 $x$ , 根据后验分布 $g(\mu|x)$ ;
频率学派: 固定 $\mu$ , 调整 $x$ ;

比较清单:

(1) 贝叶斯推断需要先验分布 $g(\mu)$ ;
(2) 频率用一种算法 $t (x)$ 来取代先验来解决特定问题;
(3) 现代的方法, 如逻辑回归与回归树, 将融合入频率学派, 这就要比贝叶斯学派更加灵活;
(4) 给定先验分布 $g(\mu)$ 后, 后验分布 $g(\mu|x)$ 是唯一确定的;
(5) 贝叶斯学派将身家性命都赌在先验分布是正确的前提假设下了, 这是很危险的做法; 频率学派则相对保守, 他们尽力地做更好, 但是至少不会做得太差, 无论 $\mu$ 长什么样子;
(6) 贝叶斯学派一次性回答完所有可能的问题, 而频率学派着重于最需要解决地问题;
(7) 相对来说贝叶斯学派的方法更简单, 也更吸引人;
(8) 在没有可信的先验信息时, 也可以使用无信息先验来解决问题;

4 费雪推断与最大似然估计 Fisherian Inference and Maximum Likelihood Estimation

4.1 似然与最大似然 Likelihood and Maximum Likelihood

对数似然函数: $l_x(\mu)=\log\{f_\mu(x)\}\tag{4.1}$
最大似然估计量: ${\rm MLE}:\hat\mu=\argmax_{\mu\in\Omega}\{l_x(\mu)\}\tag{4.2}$

事实上 $\hat\mu$ 未必存在, 或者可能存在多个最大值点, 但是此处仍然假设 $\hat\mu$ 是唯一存在的;
对于最大似然估计量的函数值 $\theta=T(\mu)$ , 可以使用plug-in principle进行最大似然估计: $\hat\theta=T(\hat\mu)\tag{4.3}$
最大似然估计流行的三个原因:
- (1) MLE算法可以自动化运行, 很容易写成脚本;
- (2) MLE的频率学性质非常好, 在大样本的情况下几乎是无偏的, 且MLE的方差也基本是最小的;
  - 根据Cram-Rao lower bound定理, 估计量 $\hat\theta$ 的下届为: $var_\theta(\hat\theta)\ge\frac{1}{n\mathcal{I}_\theta}\tag{4.33}$ , 恰为MLE渐近分布的方差;
- (3) MLE又合理的贝叶斯转换形式, 在贝叶斯法则(Formualr 3.7)中有: $g(\mu|x)=c_xg(\mu)e^{l_x(\mu)}\tag{4.4}$ 我们发现如果先验分布 $g(\mu)$ 是均匀分布的常数, 则 $\hat\mu$ 是后验密度 $g(\mu|x)$ 的最大值点;
但是当未知参数很多时, MLE的效果就会很差;

4.2 费雪信息量与最大似然估计 Fisher Information and the MLE

定义得分函数: $\dot{l}_x(\theta)=\frac{\partial}{\partial\theta}\log f_\theta(x)=\frac{\dot(f)_\theta}{f_\theta(x)}\tag{4.14}$ 其中函数上方加一个点表示对 $\theta$ 求偏导;

(1) 得分函数的期望为零: $\int_{\mathcal{X}}\dot{l}_x(\theta)f_\theta(x){\rm d}x=\int_{\mathcal(X)}\dot{f}_\theta(x){\rm d}x=\frac{\partial}{\partial\theta}\int_{\mathcal{X}}f_\theta(x){\rm d}x=\frac{\partial}{\partial\theta}1=0\tag{4.15}$
(2) 定义费雪信息量: $\mathcal{I}_\theta=\int_{\mathcal{X}}\dot{l}_x(\theta)^2f_\theta(x){\rm d}x\tag{4.16}$ 则有得分函数的分布为: $\dot{l}_x(\theta)\sim(0,\mathcal{I}_\theta)\tag{4.17}$ 即得分函数的均值为零, 方差为费雪信息量;
(3) 最大似然估计量 $\hat\theta$ 近似服从均值为 $\theta$ , 方差为 $\frac{1}{\mathcal{I}_\theta}$ 的正态分布: $\hat\theta\dot{\sim}\mathcal{N}(\theta,\frac{1}{\mathcal{I}_\theta})\tag{4.18}$
(4) 得分函数关于 $\theta$ 再求一次偏导(即对数似然函数关于 $\theta$ 的二次偏导)的期望值为 $KaTeX parse error: Expected 'EOF', got '}' at position 20: …thcal{I}_\theta}̲$ : $KaTeX parse error: Expected group after '\right' at position 40: …x(\theta)\right}̲=-\mathcal{I}_\…$
总体(样本容量为 $n$ )信息量是单个样本信息量的 $n$ 倍;

关于Cram-Rao lower bound定理的证明: $\int(t(\bm{x})-\theta)^2f_\theta(\bm{x})\mathrm{d}\bm{x}\int\dot{l}_{\bm{x}}(\theta)^2f_\theta(\bm{x})\mathrm{d}\bm{x}\ge\left[\int(t(\bm{x})-\theta)\dot{l}_{\bm{x}}(\theta)f_\theta(\bm{x})\mathrm{d}\bm{x}\right]=1$ 其中 $\bm{x}=(x_1,x_2,...,x_n)$ 为样本数据集, 这里使用的是柯西不等式;

4.3 条件推断 Conditional Inference

一个简单的示例:

假定一组独立同分布样本: $x_i\sim\mathcal{N}(\theta,1)\quad i=1,2,...,n\tag{4.34}$ 取 $\theta$ 的估计量 $\hat\theta=\bar x$ , 观察员通过抛硬币的方式来决定究竟进行多少次采样: $n=25\quad{\rm probability}\space\frac{1}{2}\\n=100\quad{\rm probability}\space\frac{1}{2}\tag{4.35}$ 最终采样结果是 $n = 25$ , 那么问题来了, $\hat\theta=\bar x$ 的标准差是多少?
- 如果是 $1/\sqrt{25}=0.2$ , 那么费雪就会赞成你, 这是一个条件推断;
- 如果是 $0.01+0.04)/2]^{1/2}=0.158$ , 这就是非条件的频率学派做出的回答;

另一个示例:

对于线性回归分析中, 我们想要计算线性回归方程 $y=r_{\bm{x},\bm{y}}(x)$ 的精确性, 其中 $\bm{x}$ 与 $\bm{y}$ 分别为观测到的平行样本;
考虑这个问题时我们通常是固定 $\bm{x}$ 就是我们所观察到的值, 然后再去计算回归方程的精确性; 这也是条件推断的例子;

费雪认为条件推断是更加合理的:

(1) More relevant inferences: 这显然是相关性更高的推断方式;
(1) Simpler inferences: 至少在计算上也是更加容易的, 如在线性回归示例中我们无需考虑不同协变量的相关性;

4.4 置换与随机化 Permutation and Randomization

费雪学派的方法论因为过度依赖正态样本的假设而被批判;

以之前提到的白血病案例, 47个 $\rm ALL$ 与25个 $\rm AML$ 患者(Figure 1.1), 两样本 $t$ 检验的结果为 $t$ 值3.13, 双侧显著水平为 $0.0025$ , 这些都是基于高斯或者正态的假设;
费雪提出使用置换方法处理这72个患者样本, 即每次随机分为47个和25个的不相交集合, 然后重复 $B$ 次 $t$ 值计算, 得到了 $B$ 个不同的 $t$ 值序列 $t_1^*,t_2^*,...,t_B^*$ , 则双侧置换显著水平就是: $\frac{{\rm count}(\{|t_i^*|\ge t\})}{B}$
- 即是多次实验取均值, 这样得出的结果是 $t$ 值3.13, 置换显著水平为 $0.0022$

费雪对置换显著水平的可信度做出解释:

假设我们零下架是72个独立同分布的样本: $x_i\sim f_\mu(x)\quad i=1,2,...,n$ 这里没有正态假设, 但是我们还是默认 $f_\mu(x)$ 就是 $\mathcal{N}(\theta,\sigma^2)$ ;
假设 $\bm{o}$ 是观测样本集合 $\bm{x}$ 的次序统计量, 不妨设是从小到大排列的结果, 然后去除了各自的 $\rm ALL$ 和 $\rm AML$ 标签; 那么就有 $72! / (47! 25!)$ 中方法通过划分 $\bm{o}$ 成为不相交的子集(子集元素个数分别为47与25个), 来获得 $\bm{x}$ , 且这些概率是相同的;

5 参数化模型与指数分布族 Parametric Models and Exponential Families

5.1 单变量分布族 Univariate Families

Table 5.1
Figure 5.1
Figure 5.2

5.2 多元正态分布 The Multivariate Normal Distribution

多元正态分布的密度函数:

(1) 独立同分布;
(2) 非独立且分布不同的;

Figure 5.3

关于多元变量分割的问题, 值得好好看看, 非常的有意思, 但是推导也很复杂;

5.3 多参数分布族的费雪信息量的边界 Fisher’s Information Bound for Multiparameter Families

费雪信息量向多元推广的结果;
最大似然估计量在多参数下的推广及结论;

5.4 多项分布 The Multinomial Distribution

Table 5.2
Figure 5.4
Figure 5.5

5.5 指数分布族 Exponential Families

指数分布族的性质;

PART 2 早期计算机时代的方法 Early Computer-Age Methods

6 经验贝叶斯 Empirical Bayes

经验贝叶斯是起源于二十世纪四十年代的理论;
经验贝叶斯面临的问题与其说是理论计算, 不如说是数据集的缺乏;
Chapter 15-21中的现代方法为经验贝叶斯提供更多有利的解决方案;

6.1 罗宾公式 Robbins’ Formula

车险理赔案例:

Table 6.1
Figure 6.1

6.2 消失的物种问题 The Missing-Species Problem

一个科学家在无人岛上被困了一年, 于是他在这一年时间里观察蝴蝶, 得到了Table 6.2中的数据, $x$ 表示被观察到的次数, $y$ 表示蝴蝶的类别的数量, 如有118种蝴蝶只被观察到1次, 而有3种蝴蝶被观察到24次; 一年后这位科学家获救离开了这座无人岛;

那么如果这个科学家再被困一年, 他还能发现多少新的蝴蝶物种?

Table 6.2
Table 6.3
Figure 6.2
Table 6.4

6.3 一个医学问题示例 A Medical Example

Figure 6.3
Figure 6.4
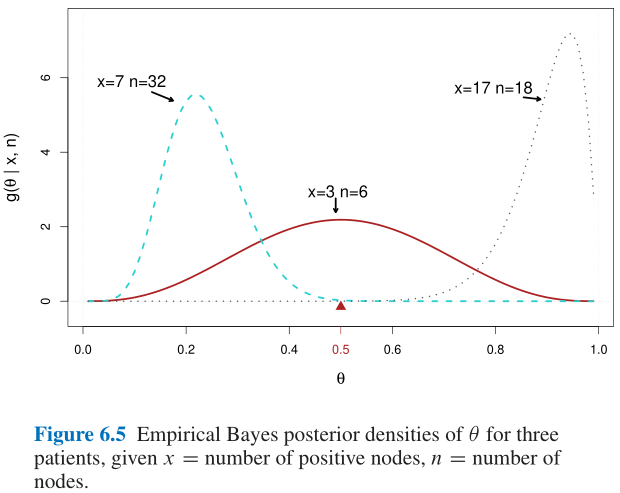
Figure 6.5

6.4 间接证据1 Indirect Evidence 1

7 詹姆斯——斯坦因估计与岭回归 James–Stein Estimation and Ridge Regression

最大似然估计的近似无偏性其实在多参数情况下容易使得估计效果非常差, 有时候我们需要舍弃一些无偏性而博取更多的延展性(确切地说就是为了减小拟合结果的均方误差), 在机器学习上可以认为最大似然估计在多参数的情况下容易发生过拟合导致模型在测试集上的预测效果非常的差;

7.1 詹姆斯——斯坦因估计量 The James–Stein Estimator

JS估计量就是先验贝叶斯方法的产物, 该估计量的目的是牺牲最大似然估计的无偏性以使得估计量具有较好的均方误差;

7.2 棒球运动员 The Baseball Players

Table 7.1
Figure 7.1

7.3 岭回归 Ridge Regression

岭回归简述:

岭回归是用于共线性数据分析的一种有偏估计方法, 它通过放弃最小二乘估计中部分的无偏性, 以损失部分精度为代价, 获得更可靠的回归系数;
虽然最小二乘估计量是所有线性估计量中方差最小的, 但是这个方差仍然可能较大, 而我们可以找到一个有偏估计量, 它的精度却远远高于无偏估计量, 岭回归就是通过在回归方程中引入有偏常数来实现这一点:
线性回归方程: $\bm{y}=\bm{X}\beta+\bm{\epsilon}$ 通常使用 $\hat\beta=\argmin_{\beta}\left\{\left\|\bm{y}-\bm{X}\beta\right\|^2\right\}$ 来估计 $\beta$ 的值: $\hat\beta=(\bm{X}^\top\bm{X})^{-1}\bm{X}^\top\bm{y}$ 但是当 $\bm{X}^\top\bm{X}$ 的行列式接近零时, $(\bm{X}^\top\bm{X})^{-1}$ 的误差会非常大, 传统的最小二乘法将不再适合用于参数估计; 此时我们可以引入一个正则项, 得到: $\hat\beta=\argmin_{\beta}\left\{\left\|\bm{y}-\bm{X}\beta\right\|^2+\left\|\bm{\Gamma}\beta\right\|^2\right\}$ 来解决这个问题; 如设 $\bm{\Gamma}=\alpha\bm{I}$ , 那么就可以得到 $\hat\beta=(\bm{X}^\top\bm{X}+\alpha\bm{I})^{-1}\bm{X}^\top\bm{y}$ 这样就可以解决上面的问题, 且当 $\alpha$ 增大, 估计值 $\hat\beta$ 的相对于真实值的偏差也会越来越大, 这就是岭回归法;

7.4 间接证据2 Indirect Evidence 2

8 广义线性回归与回归树 Generalized Linear Models and Regression Trees

8.1 逻辑回归 Logistic Regression

逻辑回归(logistic regression)是一种专门用于频数或频率型数据的回归分析方法; 其中的logit参数 $\lambda$ 定义为: $\lambda=\log\left\{\frac{\pi}{1-\pi}\right\}\tag{8.4}$ 其中 $\pi$ 为计数事件发生的频率, 即二项分布 $B i (n, p)$ 中的概率参数 $p$ ; 当 $\pi$ 从 $0$ 变化到 $1$ 时, logit参数 $\lambda$ 从 $-\infty$ 变化到 $+\infty$ ;

究其本质, 逻辑回归就是假设应变量 $\pi$ 与自变量 $x$ 间的关系并非线性, 因此构造 $\lambda$ 使得 $\lambda$ 与 $x$ 之间的存在线性关系, 然后通过拟合 $\lambda$ 与 $x$ , 再根据 $\lambda$ 与 $\pi$ 之间的关系来解决 $\pi$ 与 $x$ 之间的回归方程;
从结果上来看, 逻辑回归的目标函数是最小化Kullback–Leibler距离; 因此也是可以与Lasso回归等添加正则项的方法相结合; 本质上逻辑回归中的训练参数与线性回归中的训练参数是一致的, 正则项可以设为待定参数的某种模数;
逻辑回归是广义线性模型的一种特殊情况;
逻辑回归中的link function是: $g(y)=\frac{e^y}{e^y+1}$
- link function的反函数称为logit function: $g^{-1}(\theta)=\log\left\{\frac{\theta}{1-\theta}\right\}$ 其中 $\frac{\theta}{1-\theta}$ 称为odds;
估计参数 $\theta$ 的表达式可以写作: $\theta(\bm{X})=g(\bm{X}\beta)=\frac{e^{\bm{X}\beta}}{1+e^{\bm{X}\beta}}=\frac{1}{1+e^{-\bm{X}\beta}}$

逻辑回归的本质是在最小化KL距离;

8.2 广义线性模型 Generalized Linear Models

这部分简单来说就是针对指数分布族: $f(y)=e^{\lambda y-b(\lambda)}$ 构建自然参数 $\lambda$ 与充分统计量 $y$ 之间的线性回归;
如逻辑回归就是将二项分布 $B(n,\pi)$ 的自然参数 $\lambda=\log\frac{\pi}{1-pi}$ 与自然参数 $y = x$ 之间构建线性回归; 同理泊松回归针对的即为泊松分布 ${\rm Poi}(\theta)$ 下的自然参数 $\lambda=\log\theta$ 与充分统计量 $y = x$ 之间构建线性回归;

Table 8.4
Figure 8.3

8.3 泊松分布 Poisson Regression

其实可以发现, 所谓的link function就是Table 8.4中的自然参数 $\lambda$ 的表达式, 它的反函数就是link function, 所以泊松回归的link function就是 $\lambda(\bm{X}\beta)=e^{\bm{X}\beta}$ , 其中 $Y\sim{\rm Poisson}(\lambda)$ ;
对于泊松回归的误差值可以用 $Z={\rm sign}(y-\hat\mu)D(y,\hat\mu)^{\frac{1}{2}}\tag{8.41}$ 来衡量, 其中 $D(y,\hat\mu)$ 可以从Table 8.4中获得计算公式, 在本节的谱线红移案例中可以将 $S=\sum_{jk}Z_{jk}^2$ 作为总误差值, 其实这个数值非常的大( $S = 610$ ), 所以在实际回归分析中需要通过加入更多的高次项, 来扩充解释变量 $\bm{X}$ 的维度;

8.4 回归树 Regression Trees

Figure 8.6

书上介绍的是CART算法, 即每次分枝的目标函数是使得两个新叶子节点下的两个样本的样本方差值之和尽可能的小; 最终停止条件由交叉验证结果决定, 回归预测值由叶子节点中的所有样本均值决定; 还是比较简单的;
回归树的性质:

(1) 回归树是具有较强的可解释性;
(2) 回归树得到的regression surface是不连续的, 如Figure 8.6所示;
(3) 与广义线性模型想必, 回归树是完全无参的(nonparametric);

9 生存分析与期望最大化算法 Survival Analysis and the EM Algorithm

本章李卫明没有讲;
生存分析大致是几何分布问题, 即事件第一次发生的时间点分布;
期望最大化算法即经典的EM算法, 这个在网上可以寻找到大量的实例;

9.1 寿命表与危险率 Life Tables and Hazard Rates

9.2 删失数据与卡普兰——梅尔估计 Censored Data and the Kaplan–Meier Estimate

9.3 对数排名检验 The Log-Rank Test

9.4 比例危险模型 The Proportional Hazards Model

9.5 数据缺失与期望最大化算法 Missing Data and the EM Algorithm

10 刀切法与自助法 The Jackknife and the Bootstrap

jackknif: 利用计算机来进行标准误差计算的无公式化方法;
bootstrap: 进一步利用计算机来实现一大批包括标准误差在内的推断的自动化计算;

10.1 刀切法估计的标准误差 The Jackknife Estimate of Standard Error

注意Jackknife相对于Bootstrap的标准误差要反直觉一些:

后者直接就是标准差的计算方法, 除以 $B - 1$ ;
前者则是乘以 $\frac{n}{n-1}$ ;

jackknife的标准误差本质是方向导数;

10.2 无参自助法 The Nonparametric Bootstrap

无参自助法意思是直接以采得的样本构建虚拟分布 $\hat F$ (比如 $n$ 个样本则得到分布列为 $n$ 的等权离散分布), 从该虚拟分布中重采样进行分析;
有参自助法则是基于已知样本服从的分布 $F$ (如已知样本是来自正态分布), 但是 $F$ 中存在未知参数(如正态分布的均值参数未知), 可使用已知样本将未知参数估计出来(使用最大似然估计), 然后从确定参数的 $F$ 中进行重采样分析;

10.3 重采样计划 Resampling Plans

本节讲述的是非等权重重采样的结果, 事实上jackknife可以视为一种非等权重重采样的bootstrap;

10.4 有参自助法 The Parametric Bootstrap

见本章第一节关于有参自助法的描述;

10.5 影响函数与鲁棒估计 Influence Functions and Robust Estimation

非常困难, 完全不能理解;

11 自助法的置信区间 Bootstrap Confidence Intervals

11.1 黎曼对于单参数问题的构建 Neyman’s Construction for One-Parameter Problems

本节就是在讲置信区间的传统求解方法(默认正态分布, 正负1.96个标准误差);

11.2 分位数方法 The Percentile Method

常规的正常的置信区间分位数求法;
这里提到可以用bootstrap方法来估计分位数;

11.3 偏差矫正后的置信区间 Bias-Corrected Confidence Intervals

事实上bootstrap方法所得到的置信区间偏高, 需要做相应的调整;

11.4 二次精确度 Second-Order Accuracy

这里主要是 $\rm BC_a$ 方法, 即上一节 $\rm BC$ 方法的改良版本;

11.5 自助法的 $t$ 区间 Bootstrap- $t$ Intervals

**Bootstrap- $t$ **区间是通过多次重采样, 得出 $t$ 统计量在仿真结果上的分位数结果, 然后根据这个分位数来决定置信区间;

11.6 目标贝叶斯区间与置信分布 Objective Bayes Intervals and the Confidence Distribution

贝叶斯置信区间的求法, 重点就是要找到Formular 11.63中的置信密度(confidence)函数 $\tilde{g}_\bm{x}(\theta)$ , 然后在这个置信密度函数上两边分别割掉面积为 $0.025$ 的长尾, 中间剩下的区间就是 $95\%$ 的置信区间;

12 交叉检验与预测误差的 $C_p$ 估计 Cross-Validation and $C_p$ Estimates of Prediction Error

本章着重研究如何对预测模型的预测结果进行精确性的估计:

(1) 方法一: 传统的交叉验证, 这种方法广泛使用, 且是完全无参数化的(nonparametric);
(2) 方法二: 两种应用场景相对较少的, 但是效果非常好的参数化方法;
- ① 马洛斯 $C_p$ 估计量: Mallows’ $C_p$ estimate;
- ② 赤池信息准则(AIC): Akaike Information Criterion;

12.1 预测规则 Prediction Rules

典型的预测问题一般是根据一个有 $N$ 个样本对的训练集: $\bm{d}=\{(x_i,y_i),i=1,2,...,N\}\tag{12.1}$ 其中 $x_i$ 是一个包含 $p$ 个预测因子(predictors)的向量, $y_i$ 是一个真实的标签值(response); 通过训练集 $\bm{d}$ 学习到一个预测规则(prediction rule) $r_\bm{d}(x)$ , 使得可以在样本空间 $\mathcal{X}$ 上进行预测: $\hat y=r_\bm{d}(x)\quad x\in\mathcal{X}\tag{12.2}$ 推断任务是评估该预测规则 $r_\bm{d}(x)$ 的精确度;
常用的预测误差评估方法:

(1) 平方误差: $D(y,\hat y)=(y-\hat y)^2\tag{12.4}$
(2) 分类误差: $D(y,\hat y2)=\left\{\begin{aligned}1\quad{\rm if}\space y\neq\hat y\\0\quad{\rm if}\space y=\hat y\end{aligned}\right.\tag{12.5}$

假设训练集 $\bm{d}$ 中的每一对数据 $x_i,y_i)$ 都是从某个定义在 $\mathcal{R}^{p+1}$ 上的分布 $F$ 中随机采样得到的: $(x_i,y_i)\overset{iid}{\sim}F\quad i=1,2,...,N\tag{12.6}$

true error rate: $r_\bm{d}(x)$ 的真实误差率 ${\rm Err}_\bm{d}$ 定义如下: ${\rm Err}_\bm{d}=E_F\{D(y_0,\hat y_0)\}\tag{12.7}$ 其中 $x_0,y_0)$ 是从分布 $F$ 中独立于训练集 $bm{d}$ 随机采样得到的一个随机样本; 预测值 $\hat y_0=r_\bm{d}(x_0)$ 通过训练得到的预测规则 $r_\bm{d}$ 生成;
Figure 12.1中给出了一组超新星数据的散点图;

12.2 交叉检验 Cross-Validation

留一法与K折法;

12.3 协方差惩罚 Covariance Penalties

协方差惩罚指预测模型在训练集上和测试集上误差值之间的差距, 测试集上的误差当然要比训练集上大, 因为训练集的目标就是减少损失函数值(误差值为两倍的协方差), 正如P.219的引理Formula 12.39所示;

12.4 训练, 验证与短暂预测因子 Training, Validation, and Ephemeral Predictors

跳过, 暂时觉得用处不大;

13 目标贝叶斯推断与马尔科夫链蒙特卡洛法 Objective Bayes Inference and MCMC

13.1 目标先验分布 Objective Prior Distributions

13.2 共轭先验分布 Conjugate Prior Distributions

13.3 模型选择与贝叶斯信息标准 Model Selection and the Bayesian Information Criterion

13.4 基比斯采样与马尔科夫链蒙特卡洛法 Gibbs Sampling and MCMC

13.5 示例: 人口混合建模 Example: Modeling Population Admixture

14 战后统计推断与方法论 Postwar Statistical Inference and Methodology

PART 3 二十一世纪的话题 Twenty-First-Century Topics

15 大规模假设检验与错误发现率 Large-Scale Hypothesis Testing and FDRs

15.1 大规模检验 Large-Scale Testing

15.2 错误发现率 False-Discovery Rates

15.3 经验贝叶斯与大规模检验 Empirical Bayes Large-Scale Testing

15.4 局部错误发现率 Local False-Discovery Rates

15.5 零分布下的选择 Choice of the Null Distribution

15.6 相关性 Relevance

16 稀疏建模与最小绝对收缩和选择运算符 Sparse Modeling and the Lasso

16.1 前向逐步回归 Forward Stepwise Regression

16.2 最小绝对收缩和选择运算符 The Lasso

16.3 拟合Lasso模型 Fitting Lasso Models

16.4 最小角度回归 Least-Angle Regression

16.5 拟合广义Lasso模型 Fitting Generalized Lasso Models

16.6 Lasso的后选择推断 Post-Selection Inference for the Lasso

16.7 联系与拓展 Connections and Extensions

17 随机森林与提升方法 Random Forests and Boosting

17.1 随机森林 Random Forests

17.2 使用平方误差损失函数来提升 Boosting with Squared-Error Loss

17.3 梯度提升 Gradient Boosting

17.4 最初的提升算法 Adaboost: the Original Boosting Algorithm

17.5 联系与拓展 Connections and Extensions

18 神经网络与深度学习 Neural Networks and Deep Learning

神经网络概述:

20世纪80年代, 神经网络的提出震惊了应用统计学界;
神经网络是一种高度参数化的(highly parametrized)模型;
Figuer 18.1中是最简单的前馈神经网络示意图:
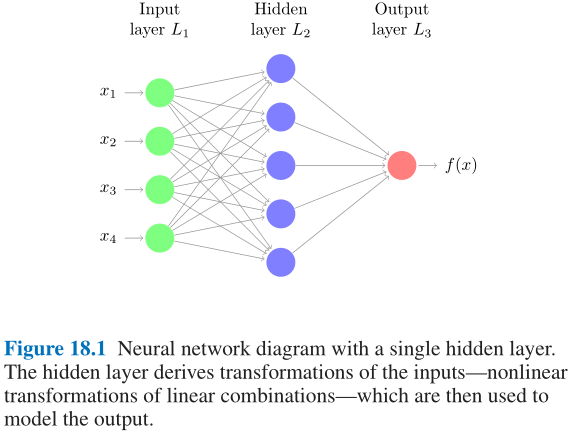
- 其中模型输入包含4个预测因子(predictors), 隐层节点共计5个, 最终输出为单个标量值; 具体计算公式如下:
  - 模型输入张量: $x_1,x_2,x_3,x_4)$
  - 计算隐层状态: $a_l=g(w_{l0}^{(1)}+\sum_{j=1}^4w_{lj}^{(1)}x_j)$
  - 计算输出标量: $o=h(w_0^{(2)}+\sum_{l=1}^5w_l^{(2)}a_l)$
- 上述公式中:
  - 称 $g$ 与 $h$ 为激活函数, 通常为非线性函数; 常见的激活函数有Sigmoid, ReLU, Softmax;
  - 称 $a_l$ 称为神经元(neurons); 神经元从数据中学习新特征的过程称为监督学习(supervised learning);
  - 每个神经元通过训练参数 ${w_{lj}^{(1)}\}_1^p$ 相互联系, 其中上标 $(1)$ 表示这是第 $1$ 层, 下标 $l j$ 表示这是第 $j$ 个变量的第 $l$ 个训练参数; 特别地, 截距项 $w_{l0}^{(1)}$ 称偏差(bias);
本质上神经网络就是一种非线性模型, 与其他线性模型的推广(广义线性模型等)并没有什么区别, 但是它确实给学界注入新鲜能量;
20世纪90年代, 随着boosting方法(Chapter 17)与支持向量机(Chapter 19)的兴起, 神经网络由于其解释性的缺乏逐渐没落;
2010年之后, 神经网络又突然以深度学习(deep learning)的身份重生, 再次制霸各类分类预测领域, 如图像与音像数据分类, 自然语言处理等;

18.1 神经网络与手写数字问题 Neural Networks and the Handwritten Digit Problem

本节从光学字符识别(optical character recognition, 下简称为OCR)任务中进行牛刀小式(积累一个俚语表达: cut one’s baby teeth);

Figure 18.2是经典手写数字数据集MNIST中的样例(该数据集可以直接通过Python的keras库模块中的相关模块获得: from keras.datasets import mnist, sklearn库中也有相应的接口):
- 每张手写数字图像为 $28\times28=784$ 像素的黑白图片: $x\in\mathbb{R}^{28\times28}$
- 每个像素点的取值范围是 ${0,1,2,...,255\}$ 的八位二进制表示;
- 每张手写数字图像的分类标签 $C(x)\in\{0,1,2,3,4,5,6,7,8,9\}$ ;
- 训练集有 $60000$ 张图像, 测试集有 $10000$ 张图像;
- 神经网络的目的即是学习概率函数 $\Pr(y=j|x),j=0,1,2,...,9$
Figure 18.3中的3层隐层架构神经网络就是典型的用于处理这种手写数字识别的经典神经网络配置:
- 第 $1$ 层到第 $2$ 层可以表达为: $z_l^{(2)}=w_{l0}^{(1)}+\sum_{j=1}^pw_{lj}^{(1)}x_j\tag{18.1}$ $a_l^{(2)}=g^{(2)}(z_l^{(2)})\tag{18.2}$ 同理第 $k - 1$ 层到第 $k$ 层可以表达为: $z_l^{(k)}=w_{l0}^{(k-1)}+\sum_{j=1}^{p_k-1}w_{lj}^{(k-1)}a_j^{(k-1)}\tag{18.3}$ $a_l^{(k)}=g^{(k)}(z_l^{(k)})\tag{18.4}$ 将上述公式使用张量表达则可以改写作: $z^{(k)}=\bm{W}^{(k-1)}a^{(k-1)}\tag{18.5}$ $a^{(k)}=g^{(k)}(z^{(k)})\tag{18.6}$ 其中 $\bm{W}^{(k-1)}$ 就是从网络层 $L_{k-1}$ 到网络层 $L_k$ 的权重矩阵, 注意这里已经把偏差截距项 $w_{l0}^{(k-1)}$ 加到 $\bm{W}^{(k-1)}$ 中了, 因此 $a^{(k)}$ 张量的第一个位置是常数 $1$ ;
- 该神经网络的最后输出层是多分类输出, 常见的激活函数为Softmax: $g^{(K)}(z_m^{(K)};z^{(K)})=\frac{e^{z_m^{(K)}}}{\sum_{l=1}^Me^{z_l^{(K)}}}\tag{18.7}$

18.2 拟合神经网络 Fitting a Neural Network

拟合神经网络本质是在最小化损失函数与正则项的累和: $\mathop{\rm minimize}\limits_{\mathcal{W}}\left\{\frac{1}{n}\sum_{i=1}^nL[y_i,f(x_i;\mathcal{W})]+\lambda J(\mathcal{W})\right\}\tag{18.8}$ 其中 $J(\mathcal{W})$

Formular 18.8说明:
- $f(x;\mathcal{W})$ 是神经网络的抽象的表达, 其中 $\mathcal{W}$ 是神经网络中所有权重矩阵构成的参数集合;
- $L [y, f (x)]$ 为损失函数, 其中 $f (x)$ 即为神经网络的预测值, $y$ 为真实值(ground truth);
- $J(\mathcal{W})$ 是一个与权重矩阵构成的参数集合 $\mathcal{W}$ 相关的非负正则项;
- $\lambda\ge0$ 是超参数, 用于控制正则项的权重; 实际情况中可能会有多个正则项, 每个正则项对应不同的超参数 $\lambda$ ;
在Chapter 7中的Formular 7.41中提到岭回归的二次正则项: $J(\mathcal{W})=\frac{1}{2}\sum_{k=1}^{K-1}\sum_{j=1}^{p_k}\sum_{l=1}^{p_k+1}\left\{w_{lj}^{(k)}\right\}^2\tag{18.9}$ 另外Chapter 16中提到的Lasso回归的惩罚项也是流行的方法;
如果是二分类问题, 则可以取损失函数 $L$ 为Formular 8.14所示的二项偏差(binomial deviance), 此时神经网络等价于带惩罚项的逻辑回归;
事实上找到Formular 18.8的全局最优点是非常困难的, 因此我们通常试图取寻找较好的局部最优解, 大部分优化方法都是在梯度下降的基础做一些增强(积累一个俚语表达: bells and whistles);

梯度计算: 反向传播(backpropagation);

Algorithm 18.1中是反向传播算法的详细说明:
- 反向传播算法说明:
  - (1) 给定训练集中的一对样本 $(x, y)$ , 首先进行在神经网络中进行前馈计算, 此时每层的节点 $a_l^{(k)}$ 中都被激活, 包括最后的输出层;
  - (2) 然后计算输出层的误差项 $\delta_l^{(K)}$ , 这就是简单的预测误差, 如Formular 18.10所示;
  - (3) 对于非输出层的隐层, 也可以计算误差项 $\delta_l^{(k)},k=K-1,K-2,...,2$ , 方法是将输出的误差值反向传播, 以下一层误差值作为该层的输入, 不断将误差传播到输入层, 如Formular 18.11所示;
  - (4) 此处的技巧如Formular 18.12所示, 即可以通过残差 $\delta$ 快速计算偏导值;

梯度下降:

(1) 随机梯度下降(SGD): Stochastic Gradient Descent, 每次选取若干参数进行梯度下降, 而非每次优化所有参数, 可以大大降低梯度计算的代价;
(2) 加速梯度方法(AGM): Accelerated Gradient Methods, 每次梯度下降在约定的下降方向上额外增加步长, 如经典的momentum方法;
(3) 模拟退火: Rate Annealing, 优化的步长应当逐渐减小;