最小平方误差的求值

 

    在很多问题里，通常要找到一个系数 a ，使得给定的误差函数值形如 f(d(x,a)-t) 期望最少，其中 t 为真实值， d(x,a) 是关于自变量 x ，系数为 a 的函数 ( 通常是线性函数 )( 注： x 和 a 通常是向量，表示一组自变量和对应的一组系数 ) 。给定的误差函数可以是误差的绝对值期望，也可以是误差值的平方的期望。通常平方比绝对值更常用，因为方便做微分运算。

    对于平方误差函数 E = Σ (d(x,a) – t(x) )² ，它的最小值称为最小均方误差 (MMSE) ，我们经常要求函数 d(x,a) 中系数 a ，使得误差最小，从而做出判断。例如在信源最优量化中，需要寻找一个最优量化值，用来代表附近范围的值，使得误差最小。在视频运动估计，预测编码等应用中，找出最好的预测值，使得与真实值最接近。在曲线拟合中，需要估计出一条曲线方程，使得样本点集与曲线上的估计值的均方误差最小，这种最小平方拟合也译作最小二乘法。 ( 又是高斯这大牛搞出来的 )

    为求局部极小值，对误差方程求导，使导数为 0 ，可得到关于系数向量 a 线性方程组，解出线性方程组便得到的解为最优的系数，参见：

   http://www.tyut.edu.cn/kecheng/jisff/dzja/ch6/ch6-1.htm

  

   然而，有时候很难或不可能得到方程组的显式解。我们可以用迭代逼近的方法寻找函数的最小值。一种常用的方法成为 ” 梯度下降法 ”(gradient descent method) ，也称最速下降法。

http://mathworld.wolfram.com/MethodofSteepestDescent.html

以一维情况为例，我们首先估计一个初始系数值 a⁰, 然后求出误差函数的在该点导数f'(x) , 迭代直到第r步系数值 a^r, 使该点梯度绝对值小于某一精度阀值。

   a^r = a^r-1 – k f'(x) | _a^r-1

 

  

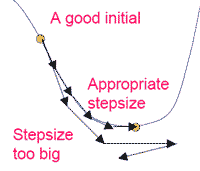
    其中k为速度常数，取过大会使在极值点附近振荡，过小则迭代次数太多。

    对于多维的情况，则利用 Jacobi 矩阵计算偏导数。

   更复杂的方法有共轭梯度法，牛顿 - 拉夫逊 (Newton-Raphson, N-R 法 ) ，  Levenberg-Marquardt方法

关于共轭梯度法求函数最小值的方法，有一篇很好的指导文章：

http://www.cs.utah.edu/classes/cs3200/notes/painless-conjugate-gradient.pdf

CMU计算机系写的共轭梯度法解惑，非常详细地讨论了梯度下降和共轭梯度法，还有一些线性代数的复习。

关于Levenberg- Marquardt的C＋＋程序：

http://www.ics.forth.gr/~lourakis/levmar/

关于他的原理：

http://www.cs.toronto.edu/~roweis/notes/lm.pdf