Fisher 线性分类器由R.A.Fisher在1936年提出,至今都有很大的研究意义,下面介绍Fisher分类器的Fisher准则函数
Fisher准则函数
在模式识别的分类算法中,大概可以分为两类,一种是基于贝叶斯理论的分类器,该类型分类器也称为参数判别方法,根据是基于贝叶斯理论的分类器必须根据所提供的样本数据求出先验概率和类概率密度函数的类型和参数;另一种是非参数判别方法,它倾向于由所提供样本数据直接求出在某一准则函数下的最优参数,这种方法必须由分类器设计者首先确定准则函数,并根据样本数据和该函数最优的原理求出函数的参数。基于贝叶斯理论的分类器对于设计者来说比较死板和原则,它必须知道类概率密度函数和先验概率才能估算出判别函数,但是实际上样本数据的类概率密度函数的类型和参数都是不知道的,这给参数判别方法带来了麻烦;而非参数方法的优点在于,当设计者设计好准则函数之后,便可用样本数据优化分类器参数,难点在于准则函数的设计,因此,两种方法各有千秋,互为补充!
设样本d维特征空间中描述,则两类别问题中线性判别函数的一般形式可表示成
 ,其中WT表示垂直于超平面的法向量,在二维的情况下,便是判别直线的法向量,W0称为阈权值,它只决定超平面在空间上的上下或者左右平移的位置。
,其中WT表示垂直于超平面的法向量,在二维的情况下,便是判别直线的法向量,W0称为阈权值,它只决定超平面在空间上的上下或者左右平移的位置。
在使用线性分类器时,样本的分类由其判别函数值决定,而每个样本的判别函数值是其各分量的线性加权和再加上一阈值w0。如果我们只考虑各分量的线性加权和,则它是各样本向量与向量W的向量点积。如果向量W的幅度为单位长度,则线性加权和又可看作各样本向量在向量W上的投影。显然样本集中向量投影的分布情况与所选择的W向量有关。如下图:

图1
红色跟蓝色分别为两类样本,显然,从分类的角度来看,W1要比W2要好,因此,Fisher准则函数的基本思路是向量W的方向选择应能使两类样本投影的均值之差尽可能大些,而使类内样本的离散程度尽可能小。
为了给出Fisher准则函数的数学定义,我们必须定义一些基本参量,如下:
1 样本在d维特征空间的一些描述量。
(1) 各类样本均值向量mi

(2) 样本类内离散度矩阵Si与总类内离散度矩阵Sw

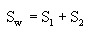
注释:类内离散矩阵Si在形式上与协方差矩阵很相似,但协方差矩阵是一种期望值,而类内离散矩阵只是表示有限个样本在空间分布的离散程度
2 在一维Y空间
(1) 各类样本均值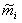
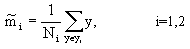
(2) 样本类内离散度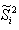 和总类内离散度
和总类内离散度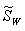
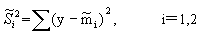
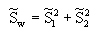
在定义了上述一系列描述量后,可以用这些量给出Fisher准则的函数形式。根据Fisher选择投影方向W的原则,即使原样本向量在该方向上的投影能兼顾类间分布尽可能分开,类内样本投影尽可能密集的要求,用以评价投影方向W的函数为:
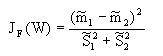
显然,准则函数的函数值跟总类内离散度成反比,跟样本差值的均方成正比,也就说,两类样本的均值相差越大,函数值越大,反之,则越小,类内离散度越小,函数值越大,反之则越小。同一类的样本,离散度应该要小。
各最优参数的确定
前面已提到,在非参数判别分类方法中,首先必须确定准则函数(假设样本是线性可分的),然后根据样本集求出使得准则函数达到极值的分类器参数,对于线性分类器,其典型形式为: ,因此需要确定WT和wo两个分类器参数。
,因此需要确定WT和wo两个分类器参数。
2、分类器参数的确定
关于Fisher的上一篇文章提到,其准则函数为

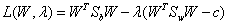
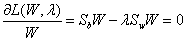

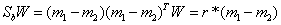
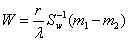
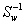 线性变换上,其中Sw为总类内离散度。
线性变换上,其中Sw为总类内离散度。
3.1、知道先验概率P(W1)和P(W2)若知道先验概率和各样本数量,可以根据以下公式计算W0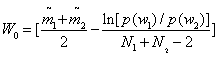

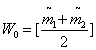


























 3417
3417

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








