Preface
主要内容:
Exponential Family(指数分布族)
Generalized Linear Models(广义线性模型)
Softmax Regression
Exponential Family
首先,我们回忆一下前面几节课所讲的内容,主要是通过高斯分布和伯努力分布进而推导出最小二乘法概率模型与逻辑回归概率模型。
y∈R:Gaussian(ϕ)→LeastSquares(1)
(1)
y
∈
R
:
G
a
u
s
s
i
a
n
(
ϕ
)
→
L
e
a
s
t
S
q
u
a
r
e
s
y∈{0,1}:Bernoulli(ϕ)→LogisticRegression(2)
(2)
y
∈
{
0
,
1
}
:
B
e
r
n
o
u
l
l
i
(
ϕ
)
→
L
o
g
i
s
t
i
c
R
e
g
r
e
s
s
i
o
n
而,高斯分布和伯努力分布都可以写成指数分布族的形式:
其中, η η 为自然参数(nature parameter), T(y) T ( y ) 是充分统计量(sufficient statistic),在一般情况下, T(y)=y T ( y ) = y 。当参数 a a , b b , T(y) T ( y ) 都固定以后,就定义了一个以 η η 为参数的函数族。
接下来以高斯分布和伯努力分布说明如何定义了一个以 η η 为参数的函数族:
1.Bernoulli Distribution
伯努利分布是对0,1分布的问题进行建模。所以,其概率密度函数如下:
即,
所以有,
η=logϕ1−ϕ(9) (9) η = l o g ϕ 1 − ϕ
ϕ=11+e−η(10) (10) ϕ = 1 1 + e − η
T(y)=y(13) (13) T ( y ) = y
b(y)=1(14) (14) b ( y ) = 1
这样我们就可以清楚地看出伯努力分布如何定义了一个以 η η 为参数的函数族。同时也说明了, y∈{0,1}:Bernoulli(ϕ)→LogisticRegression y ∈ { 0 , 1 } : B e r n o u l l i ( ϕ ) → L o g i s t i c R e g r e s s i o n 的模型函数的logistic函数的形式问题。
2.Gaussian Distribution
在线性回归模型中,
σ2
σ
2
的取值对于最后的
θ
θ
与
hθ(x)
h
θ
(
x
)
无影响,故以在这里,我们将
σ2
σ
2
取值为1。所以,高斯分布概率密度函数如下:
所以有,
η=μ(18)
(18)
η
=
μ
T(y)=y(19)
(19)
T
(
y
)
=
y
a(η)=μ2/2=η2/2(20)
(20)
a
(
η
)
=
μ
2
/
2
=
η
2
/
2
b(y)=12π√exp(−12y2)(21)
(21)
b
(
y
)
=
1
2
π
e
x
p
(
−
1
2
y
2
)
这样我们就可以清楚地看高斯分布如何定义了一个以 η η 为参数的函数族。
这样,我们就说明了高斯分布和伯努力分布属于指数分布族 。同样的还有泊松分布(用于对记数建模,例如网站的访客数量,商店的顾客数)、伽马分布与指数分布(用于正数的分布,对间隔进行建模,例如在公交站等车时的下一趟车什么时候到)、 β β 分布与Dirichlet分布(用于小数的分布,对概率分布进行建模的概率分布)、Wishart分布(协方差矩阵分布)等等都属于指数分布族。
Multinomial Distribution
多项式分布是对伯努力分布的多元扩展,主要用于解决多分类问题。多分类问题使得对于0-1问题建模的伯努力分布 y∈{0,1} y ∈ { 0 , 1 } 无法满足问题需要,进而有 y∈{1,2...k} y ∈ { 1 , 2 . . . k } 。
定义1:概率
p(y=i)=ϕi
p
(
y
=
i
)
=
ϕ
i
,为了避免过参数化所以有:
ϕi=p(y=i;ϕ)
ϕ
i
=
p
(
y
=
i
;
ϕ
)
,
k∈{1,k−1}
k
∈
{
1
,
k
−
1
}
,可以推出
ϕk=1−∑i=1k−1ϕi
ϕ
k
=
1
−
∑
i
=
1
k
−
1
ϕ
i
。
定义2:由于
T(y)≠y
T
(
y
)
≠
y
,所以
T(y)∈Rk−1
T
(
y
)
∈
R
k
−
1
,即为:
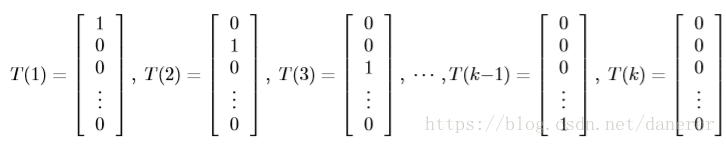
定义3: 指示器函数
1{true}=1;1{false}=0
1
{
t
r
u
e
}
=
1
;
1
{
f
a
l
s
e
}
=
0
,既有
(T(y))i=1{y=i}
(
T
(
y
)
)
i
=
1
{
y
=
i
}
,继而推得
E[(T(y))i]=P(y=i)=ϕi
E
[
(
T
(
y
)
)
i
]
=
P
(
y
=
i
)
=
ϕ
i
。
所以,多项式分布概率密度函数如下:
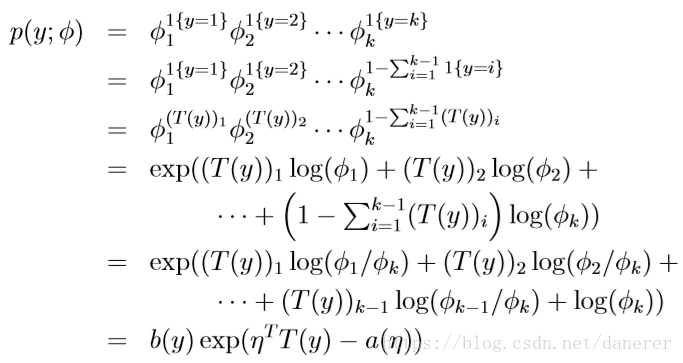
所以有,
所以,推导可得: ηi=logϕiϕk η i = l o g ϕ i ϕ k ,同时 ηk=logϕkϕk=log1=0 η k = l o g ϕ k ϕ k = l o g 1 = 0 。
继续推导:
由等式(23)
ϕkeηi=ϕi
ϕ
k
e
η
i
=
ϕ
i
可以得:
Generalized Linear Models
Three Assumptions
首先我们对于GLM(Generalized Linear Models,广义线性模型)做出下述三个假设(设计决策):
- y|x;θ∼ExponentialFamily(η) y | x ; θ ∼ E x p o n e n t i a l F a m i l y ( η ) ,假设一的式子表示变量 y y 在给定的 ,并以 θ θ 为参数下的条件概率分布,属于以自然参数 η η 的指数分布族。
- 给定 ,目标输出期望 E[T(y)|x] E [ T ( y ) | x ] ,估计函数为: h(x)=E[T(y)|x] h ( x ) = E [ T ( y ) | x ] ,一般 T(y)=y T ( y ) = y 。
- η=θTx η = θ T x ,即指数分布族中参数 η η 与输入特征 x x 满足某种线性关系。(一般而言,)
由Bernoulli Distribution到Logistic Regression模型
Step1:Bernoulli:
y|x;θ∼ExpFamily(η)
y
|
x
;
θ
∼
E
x
p
F
a
m
i
l
y
(
η
)
;
Step2:由假设二
hθ(x)=E(y|x;θ)=P(y=1|x:θ)=ϕ
h
θ
(
x
)
=
E
(
y
|
x
;
θ
)
=
P
(
y
=
1
|
x
:
θ
)
=
ϕ
;
Step3:由公式(10)
ϕ=1/(1+e−η)
ϕ
=
1
/
(
1
+
e
−
η
)
和 假设三
η=θTx
η
=
θ
T
x
;
Step4:所以
ϕ=1/(1+e−η)→ϕ=1/(1+e−θTx)
ϕ
=
1
/
(
1
+
e
−
η
)
→
ϕ
=
1
/
(
1
+
e
−
θ
T
x
)
;
Step5:
ϕ=1/(1+e−θTx)
ϕ
=
1
/
(
1
+
e
−
θ
T
x
)
就是Logistic Regression模型;
Note:
- g(η)=E[y|η]=(1+e−η)−1 g ( η ) = E [ y | η ] = ( 1 + e − η ) − 1 ,正则响应函数 。
- g(η)−1 g ( η ) − 1 ,正则关联函数。
由Gaussian Distribution到Ordinary Least Squares模型
Step1:Gaussian:
y|x;θ∼ExpFamily(η)∼N(μ,σ2)
y
|
x
;
θ
∼
E
x
p
F
a
m
i
l
y
(
η
)
∼
N
(
μ
,
σ
2
)
;
Step2:由假设二
hθ(x)=E(y|x;θ)=μ
h
θ
(
x
)
=
E
(
y
|
x
;
θ
)
=
μ
;
Step3:由公式(18)
η=μ
η
=
μ
和 假设三
η=θTx
η
=
θ
T
x
;
Step4:所以
hθ(x)=E(y|x;θ)=μ=η=θTx
h
θ
(
x
)
=
E
(
y
|
x
;
θ
)
=
μ
=
η
=
θ
T
x
;
Step5:
hθ(x)=θTx
h
θ
(
x
)
=
θ
T
x
就是Ordinary Least Squares模型;
由Multinomial Distribution到Softmax Regression模型
Step1:Multinomial :
y|x;θ∼ExpFamily(η)
y
|
x
;
θ
∼
E
x
p
F
a
m
i
l
y
(
η
)
;
Step2:由假设三
η=θTx
η
=
θ
T
x
,
;
Step3:由假设二

;
For Example:
假设有一个大小为m的训练集,它的似然函数为:
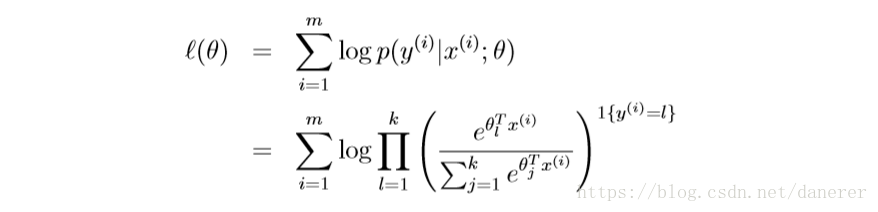
最后在在有了最大似然函数之后,我们就可以使用牛顿法或梯度法来求
θ
θ
。









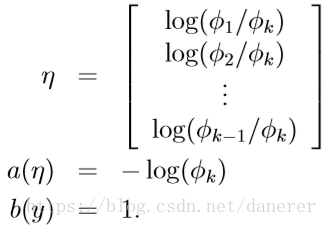














 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








