匈牙利算法与卡尔曼滤波

DCGJ666

于 2022-10-06 09:56:46 发布

阅读量941

点赞数

分类专栏：深度学习文章标签：算法机器学习 python

本文链接：https://blog.csdn.net/dcgj666/article/details/125505337

版权

深度学习专栏收录该内容

39 篇文章 1 订阅

订阅专栏

匈牙利算法与卡尔曼滤波

匈牙利算法
- 指派问题概述
- 匈牙利算法流程
卡尔曼滤波

匈牙利算法

指派问题概述

首先，对匈牙利算法解决的问题进行概述：实际中，会遇到这样的问题，有n项不同的任务，需要n个人分别完成其中的1项，每个人完成任务的时间不一样。于是就有一个问题，如何分配任务使得花费时间最少。
通俗来讲，就是n*n矩阵中，选取n个元素，每行每列各有一个元素，使得和最小。

可以抽象成一个矩阵，如果是求和最小问题，那么这个矩阵就叫做花费矩阵（Cost Matrix）；如果要求的问题是使之和最大化，那么这个矩阵就叫做利益矩阵（Profit Matrix）.

匈牙利算法流程

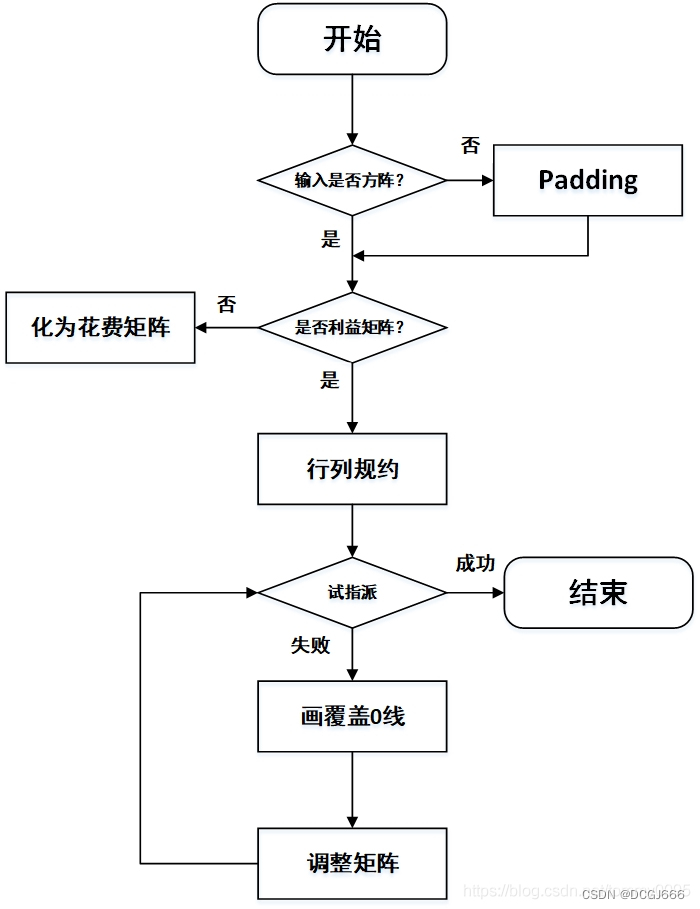
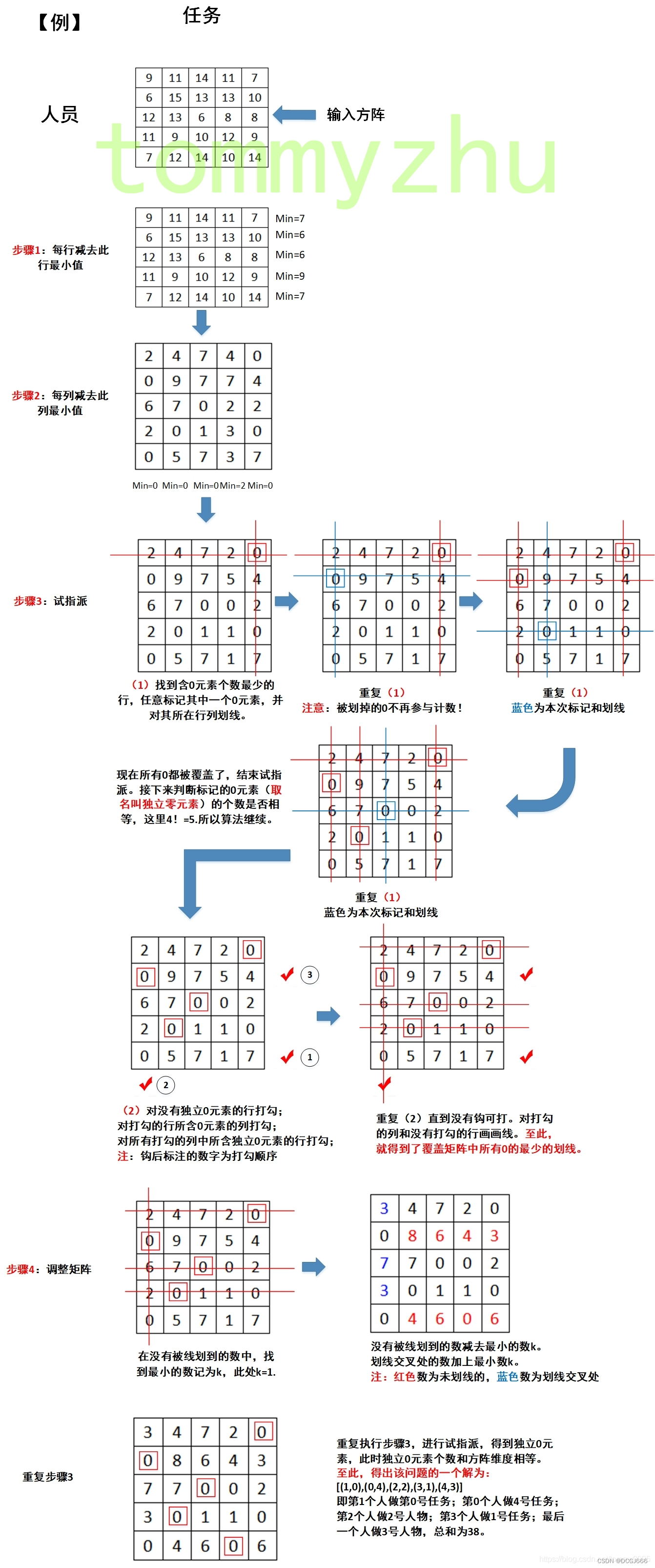
在这里插入图片描述
匈牙利算法首先进行列规约，即每行减去此行最小元素，每一列减去该列最小元素，规约后每行每列中必有0元素出现。接下来进行试指派，也就是划最少的线覆盖矩阵中全部的0元素，如果试指派的独立0元素数等于方阵维度则算法结束，如果不等于则需要对矩阵进行调整，重复式指派和调整步骤直到满足算法结束条件。
在这里插入图片描述

import numpy as np
import collections
import time

class Hungarian():
	def __init__(self, input_matrix=None, is_profit_matrix=False):
		"""
		输入为一个二维嵌套列表
		is_profit_matrix = False代表输入是消费矩阵（需要使消费最小化），反之则为利益矩阵（需要使利益最大化）
		"""
		if input_matrix is not None:
			# 保存输入
			my_matrix = np.array(input_matrix)
			self._input_matrix = np.array(input_matrix)
			self._maxColumn = my_matrix.shape[1]
			self._maxRow = my_matrix.shape[0]
			# 本算法必须作用于方阵，如果不为方阵则填充为方阵
			matrix_size = max(self._maxColumn, self._maxRow)
			pad_columns = matrix_size - self._maxRow
			pad_rows = matrix_size - self._maxColumn
			my_matrix = np.pad(my_matrix, ((0, pad_columns), (0, pad_rows)), 'constant', constant_values=(0))
			# 如果需要，则转化为消费矩阵
			if is_profit_matrix:
				my_matrix = self.make_cost_matrix(my_matrix)
			self._cost_matrix = my_matrix
			self._size = len(my_matrix)
			self._shape = my_matrix.shape
			# 存放算法结果
			self._results = []
			self._totalPotential = 0
		else:
			self._cost_matrix = None
	def make_cost_matrix(self, profit_matrix):
		'''利益矩阵转化为消费矩阵，输出为numpy矩阵'''
		# 消费矩阵 = 利益矩阵最大值组成的矩阵 - 利益矩阵
		matrix_shape = profit_matrix.shape
		offset_matrix = np.ones(matrix_shape, dtype=int) * profit_matrix.max()
		cost_matrix = offset_matrix - profit_matrix
		return cost_matrix
	def get_results(self):
		"""获取算法结果"""
		return self._results
	def calculate(self):
		"""
		实施匈牙利算法的函数
		"""
		result_matrix = self._cost_matrix.copy()
		# 步骤1：矩阵每一行减去本行的最小值
		for index, row in enumerate(result_matrix):
			result_matrix[index] -= row.min()
		# 步骤2：矩阵每一列减去本行的最小值
		for index, column in enumerate(result_matrix.T):
			result_matrix[:, index] -= column.min()
		# 步骤3：使用最少数量的划线覆盖矩阵中所有的0元素
		# 如果划线总数不等于矩阵的维度，需要进行矩阵调整并重复循环此步骤
		total_covered = 0
		while total_covered < self._size:
			time.sleep(1)
			# 使用最少数量的划线覆盖矩阵中所有的0元素同时记录划线数量
			cover_zeros = CoverZeros(result_matrix)
			single_zero_pos_list = cover_zeros.calculate()
			covered_rows = cover_zeros.get_covered_rows()
			covered_columns = cover_zeros.get_covered_columns()
			total_covered = len(covered_rows) + len(covered_columns)
			# 如果划线总数不等于矩阵的维度需要进行矩阵调整（需要使用未覆盖处的最小元素）
			if total_covered < self._size:
				result_matrix = self._adjust_matrix_by_min_uncovered_num(result_matrix, covered_rows, covered_columns)
		# 元组形式结果对存放到列表
		self._results = single_zero_pos_list
		# 计算总期望结果
		value = 0
		for row, column in single_zero_pos_list:
			value += self._input_matrix[row, column]
		self._totalPotential = value
	def get_total_potential(self):
		return self._totalPotential
	def _adjust_matrix_by_min_uncovered_num(self, result_matrix, covered_rows, covered_columns):
		"""计算未被覆盖元素中的最小值（m）,未被覆盖元素减去最小值m,行列划线交叉处加上最小值m"""
		adjusted_matrix = result_matrix
		# 计算未被覆盖元素中的最小值（m）
        elements = []
        for row_index, row in enumerate(result_matrix):
            if row_index not in covered_rows:
                for index, element in enumerate(row):
                    if index not in covered_columns:
                        elements.append(element)
        min_uncovered_num = min(elements)
        #print('min_uncovered_num:',min_uncovered_num)
        #未被覆盖元素减去最小值m
        for row_index, row in enumerate(result_matrix):
            if row_index not in covered_rows:
                for index, element in enumerate(row):
                    if index not in covered_columns:
                        adjusted_matrix[row_index,index] -= min_uncovered_num
        #print('未被覆盖元素减去最小值m',adjusted_matrix)
    
        #行列划线交叉处加上最小值m
        for row_ in covered_rows:
            for col_ in covered_columns:
                #print((row_,col_))
                adjusted_matrix[row_,col_] += min_uncovered_num
        #print('行列划线交叉处加上最小值m',adjusted_matrix)

        return adjusted_matrix

class CoverZeros():
	"""
    使用最少数量的划线覆盖矩阵中的所有零
    输入为numpy方阵
    """
    def __init__(self, matrix):
        # 找到矩阵中零的位置（输出为同维度二值矩阵，0位置为true，非0位置为false）
        self._zero_locations = (matrix == 0)
        self._zero_locations_copy = self._zero_locations.copy()
        self._shape = matrix.shape

        # 存储划线盖住的行和列
        self._covered_rows = []
        self._covered_columns = []

    def get_covered_rows(self):
        """返回覆盖行索引列表"""
        return self._covered_rows

    def get_covered_columns(self):
        """返回覆盖列索引列表"""
        return self._covered_columns

    def row_scan(self,marked_zeros):
        '''扫描矩阵每一行，找到含0元素最少的行，对任意0元素标记（独立零元素），划去标记0元素（独立零元素）所在行和列存在的0元素'''
        min_row_zero_nums = [9999999,-1]
        for index, row in enumerate(self._zero_locations_copy):#index为行号
            row_zero_nums = collections.Counter(row)[True]
            if row_zero_nums < min_row_zero_nums[0] and row_zero_nums!=0:
                #找最少0元素的行
                min_row_zero_nums = [row_zero_nums,index]
        #最少0元素的行
        row_min = self._zero_locations_copy[min_row_zero_nums[1],:]
        #找到此行中任意一个0元素的索引位置即可
        row_indices, = np.where(row_min)
        #标记该0元素
        #print('row_min',row_min)
        marked_zeros.append((min_row_zero_nums[1],row_indices[0]))
        #划去该0元素所在行和列存在的0元素
        #因为被覆盖，所以把二值矩阵_zero_locations中相应的行列全部置为false
        self._zero_locations_copy[:,row_indices[0]] = np.array([False for _ in range(self._shape[0])])
        self._zero_locations_copy[min_row_zero_nums[1],:] = np.array([False for _ in range(self._shape[0])])

    def calculate(self):
        '''进行计算'''
        #储存勾选的行和列
        ticked_row   = []
        ticked_col   = []
        marked_zeros = []
        #1、试指派并标记独立零元素
        while True:
            #print('_zero_locations_copy',self._zero_locations_copy)
            #循环直到所有零元素被处理（_zero_locations中没有true）
            if True not in self._zero_locations_copy:
                break
            self.row_scan(marked_zeros)
            
        #2、无被标记0（独立零元素）的行打勾
        independent_zero_row_list = [pos[0] for pos in marked_zeros]
        ticked_row = list(set(range(self._shape[0])) - set(independent_zero_row_list))
        #重复3,4直到不能再打勾
        TICK_FLAG = True
        while TICK_FLAG:
            #print('ticked_row:',ticked_row,'   ticked_col:',ticked_col)
            TICK_FLAG = False
            #3、对打勾的行中所含0元素的列打勾
            for row in ticked_row:
                #找到此行
                row_array = self._zero_locations[row,:]
                #找到此行中0元素的索引位置
                for i in range(len(row_array)):
                    if row_array[i] == True and i not in ticked_col:
                        ticked_col.append(i)
                        TICK_FLAG = True
            
            #4、对打勾的列中所含独立0元素的行打勾
            for row,col in marked_zeros:
                if col in ticked_col and row not in ticked_row:
                    ticked_row.append(row)
                    FLAG = True
        #对打勾的列和没有打勾的行画画线
        self._covered_rows    = list(set(range(self._shape[0])) - set(ticked_row))
        self._covered_columns = ticked_col
            



        return marked_zeros

卡尔曼滤波

现代系统大多数都配备了多个传感器，这些传感器根据一系列测量值提供隐藏变量的估计。例如，GPS接收机提供位置和速度估计，其中位置和速度是隐藏变量，卫星信号到达差值时间是测量值。

一维卡尔曼滤波

系统状态 当前状态是预测算法的输入，下一个状态（下一时间间隔的目标参数）是算法输出。
动态模型 描述输入和输出之间的关系
测量噪声 测量中包含的误差
过程噪声 动态模型误差

https://zhuanlan.zhihu.com/p/80255855

卡尔曼滤波器方程

状态更新方程 State Update Equation
这里的factor成为**卡尔曼增益（Kalman Gain）*用 $K_n$ 表示。下标n表示卡尔曼增益随每次迭代而变化。
也就是说，当前状态等于卡尔曼滤波在n时刻的预测值＋系数（n时刻测量值-n时刻的预测值）
状态外推方程（过渡方程或预测方程）
这个方程组将当前状态外推到下一个状态，即判断状态是否更新，或怎么更新。
卡尔曼增益方程

当测量不确定度非常大且估计不确定度非常小时，卡尔曼收益趋近于0.因此，我们估计值一个较大的权重，给测量值一个较小的权重。
卡尔曼增益>>通过给定的测量值改变我的估计。
卡尔曼增益越低，越依赖估计值；相反，越依赖测量值。
协方差更新方程

由于（1-Kn）<=1，我们可以很清楚的从方程中看到，随着滤波器的每次迭代，估计不确定行会变得越来越小。当测量不确定性增大，卡尔曼增益会变小，因此，估计不确定度的收敛会变慢。
协方差外推方程

利用动态模型方程进行。

总结

初始化时，当估计误差很大时，估计初值并不重要，因为这样会计算出较大的卡尔曼增益导致预测值与测量值非常接近。
如果我们使用了一个恒定系统动力模型的一维卡尔曼滤波器来测量温度变化的液体温度。我们在卡尔曼滤波器估计中观察了滞后误差。这个滞后误差是由错误的系统动力模型与错误的过程模型导致的。（ps:滞后误差可以通过合理的定义系统动力模型与过程模型得到解决）
一个较大的过程误差，能够维持协方差不会一致缩小，使得卡尔曼增益维持一个较大的水平，从而更加贴近观测值。

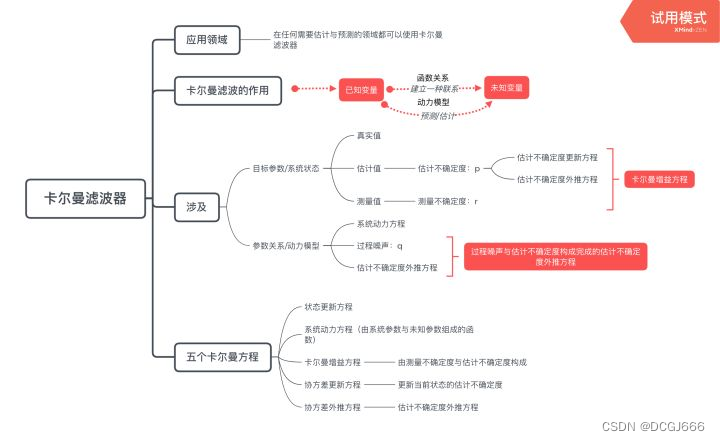
在这里插入图片描述

多维卡尔曼滤波

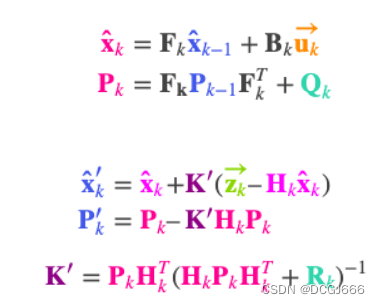
在这里插入图片描述
卡尔曼滤波的五个方程分别为：状态方程、协方差方程，状态更新方程、协方差更新方程、卡尔曼增益方程。
B：表示控制矩阵
Q：过程噪声
F：转移矩阵
z: 观测值
R：观测方差
HPH^T: 估计方差

扩展卡尔曼滤波器（EKF）

处理非线性问题
有两件事要考虑：

在不知道它的基本函数的情况下，如何从实际信号中计算一阶导数；
如何将我们的单值非线性状态/观测模型推广到我们一直在考虑的多值系统中；
如果一个信号（如传感器值z_k）是另一个信号的函数（如状态x_k），我们可以使用第一个信号的连续差除以第二个信号的连续差：

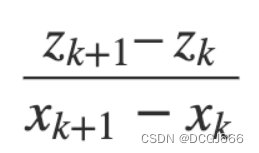
扩展卡尔曼滤波器【EKF】雅可比矩阵

雅可比矩阵
如何将我们的单值非线性状态/观测模型推广到多值系统，这将有助于我们回忆线性模型传感器组件的方程：

$z_k=Cx_k$
对于一个有两个状态值与三个传感器的系统，我们可以重写系统观测模型：
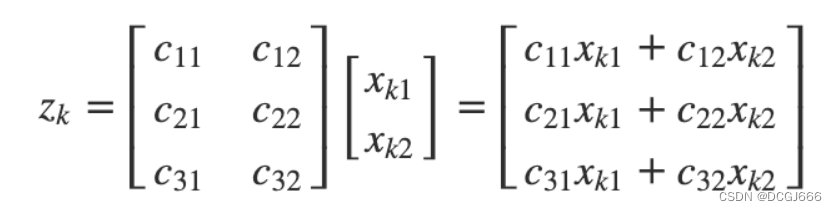
在这里插入图片描述
对于非线性模型，同样会有一个矩阵，其行数等于传感器数，列数等于状态数；但是，该矩阵将包含传感器值相对于该状态值的一阶导数的当前值。数学家将这种导数称为偏导数，并将这些导数的矩阵称为雅可比矩阵。

例如一项调查，其中一组人被要求在一个量表上对两种不同的产品进行评分。每个产品的总分将是该产品所有用户评分的平均值。为了了解一个人如何影响单个产品的整体评级，我们将查看此人对该产品的评级。每个人都像是一个偏导数，而这个人就像是雅可比矩阵。用传感器替换人，用状态替换问题，你就能理解扩展卡尔曼滤波器的传感器模型。

我们的线性模型：
$x_k=Ax_{k-1}+w_k$
变成：
$x_k=f(x_{k-1})+w_k$

在非线性的情况下，我们可以使用扩展卡尔曼滤波器（EKF），它把非线性函数在当前估计状态的平均值附近进行线性化。
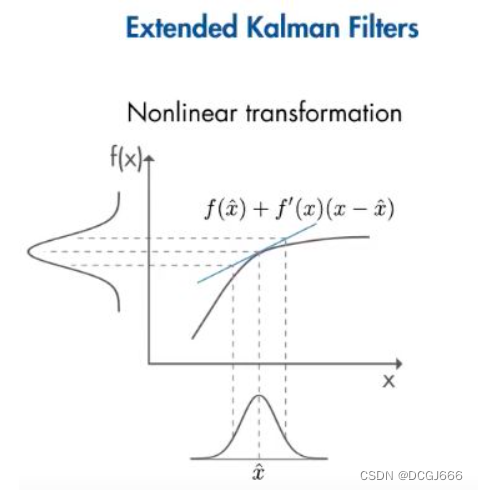
在这里插入图片描述
在每个微小时刻执行线性化，然后将得到的雅可比矩阵用于预测和更新卡尔曼滤波器的算法状态。

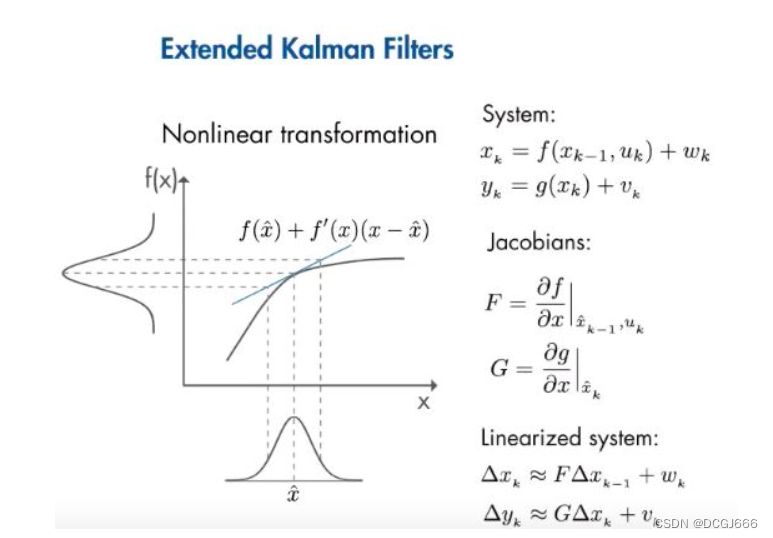
当系统是非线性的，并且可以通过线性化很好的近似时，那么扩展卡尔曼滤波器（EKF）是状态估计的一个很好的选择。
但是，扩展卡尔曼滤波器有以下缺点：

由于复杂的导数，可能难以解析计算雅可比矩阵
以数值方式计算雅可比矩阵，可能需要很高的计算成本
扩展卡尔曼滤波器不适用于不连续的系统，因为系统不可微分时，雅可比矩阵不存在
对于高度非线性化的系统，效果并不好。

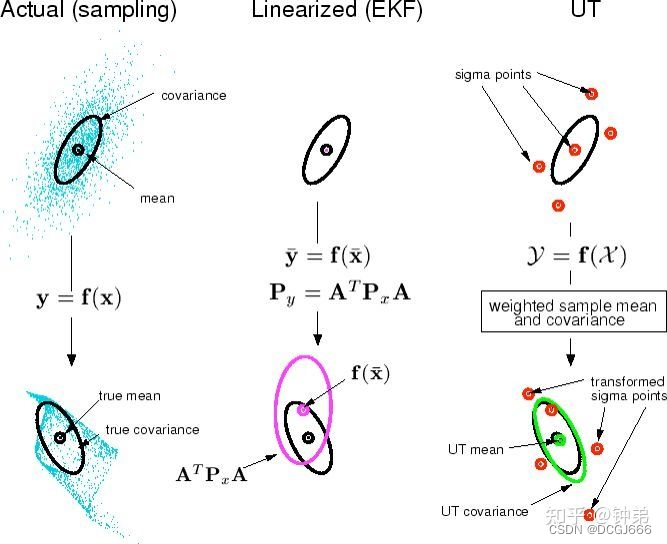
UFK 无迹卡尔曼滤波

逼近概率分布要比逼近任意的非线性函数要容易得多。
在这里插入图片描述

DCGJ666

关注

0
点赞
踩
2

收藏

觉得还不错? 一键收藏
0
评论
匈牙利算法与卡尔曼滤波

首先，对匈牙利算法解决的问题进行概述：实际中，会遇到这样的问题，有n项不同的任务，需要n个人分别完成其中的1项，每个人完成任务的时间不一样。于是就有一个问题，如何分配任务使得花费时间最少。通俗来讲，就是n*n矩阵中，选取n个元素，每行每列各有一个元素，使得和最小。可以抽象成一个矩阵，如果是求和最小问题，那么这个矩阵就叫做花费矩阵（Cost Matrix）；如果要求的问题是使之和最大化，那么这个矩阵就叫做利益矩阵（Profit Matrix）.
复制链接

扫一扫