基于混沌的可调图像加密

基于混沌模式的可调图像加密算法设计

摘要

本文提出了一种基于置乱‐扩散结构的可调彩色图像加密方案，利用分段非线性混沌映射在加密过程中生成伪随机序列。通过引入相同调整参数，同一明文图像可被加密为不同的密文图像，从而使得攻击者无法破解该方案。仅需一轮加密即可获得满意的安全性能，且有效性显著提高。我们详细描述了所提算法，并通过安全分析和仿真验证了其安全性、有效性和鲁棒性。与现有彩色图像加密方案的比较结果表明，所提出的方案具有非常优越的性能。

Keywords : 混沌系统；保密性；彩色图像加密；安全性。

1 引言

近年来，信息技术网络得到了巨大发展，使得数字图像等大文件的交换成为可能。尽管如此，此类数据（尤其是私人数据）的安全性在防止未经授权访问方面仍是一个挑战，吸引了众多研究人员的关注（Vesal 和 Fathian，2012；Yang 和 Yang，2007；Al‐Khassaweneh，2011；Choi，2014；Oladayo，2011）。

用于文本数据加密的密码系统由于图像具有强相关性和大量数据量，尤其是彩色图像，因此不适合用于图像加密。因此，在加密此类数据时需要特别注意 （Uhl 和 Pommer，2005）。根据香农（1949）的观点，混淆和扩散是消除像素间冗余和强相关性的两种主要方法。扩散通过使用密钥来改变像素值，而混淆则通过将像素分布在整个密文图像中以减少冗余（Abdullah 等，2012；Patidar 等， 2011；Al‐Khassaweneh 和 Tawalbeh，2013）。文献中已提出多种图像加密机制。近年来，由于混沌系统对初值的敏感性和非线性特性，其在密码学中的应用吸引了大量研究关注（Kocarev 等，1998；Alvarez 等，1999；Guo 等，2000； Chen 等，2003）。

Mazloom和Eftekhari‐Moghadam（2009）在一种彩色图像加密方案中使用了一种称为CNCM的耦合非线性混沌映射。Rhouma等人（2009）提出了一种基于单向耦合映射格子（OCML）的彩色图像加密方案。刘和王（2010）在一种新的利用分段线性混沌映射（PWLCM）生成密钥的彩色图像加密算法中使用了一次性密钥。卡迪尔等人（2014）提出了一种基于斜帐篷映射和六阶CNN超混沌系统的彩色图像加密方案。Tang等人（2010）在一种基于置换‐扩散结构的新型图像加密方案中使用了带时间延迟的耦合映射格子（CML）。刘和王（2011）提出了一种基于混沌的彩色图像加密方案，使用分段线性混沌映射系统对明文图像的红、绿、蓝通道的所有比特进行置乱，然后利用陈系统对置乱后的图像进行进一步混淆和扩散。Bigdeli等人（2012）在一种新型彩色图像加密算法中使用了混沌神经网络。Seyedzadeh和Mirzakuchaki（2012）耦合了二维分段非线性混沌映射，以提出一种具有非线性和耦合结构特性的新型基于混沌的图像加密算法。董（2014）提出了一种利用安全哈希算法3（SHA‐3）与初始密钥结合生成新密钥的彩色图像加密方法，从而使密钥流在每次加密过程中发生变化。

此外，帕蒂达尔等人（2010）对帕蒂达尔等人（2009）提出了修改，以使其能够抵御罗玛等人（2010）所描述的已知/选择明文攻击。为此，他们首先从密钥计算出一些称为扩散密钥的中间密钥，然后在扩散过程中使用它们。然而，李等人（2011）证明，该修改后的方案仍然存在安全弱点，无法抵御罗玛等人（2010）所述的相同已知/选择明文攻击。王等人（2012）提出了一种基于混沌逻辑映射的彩色图像加密方案混淆‐扩散；然而，所提出的方案对选择明文分析不安全（Tu 等人，2013）。

刘等人（2012）提出了一种基于DNA编码和混沌映射的RGB图像加密算法。在此方案中，使用DNA加法来扰乱彩色明文图像的像素值，然后对打乱后的图像进行加密。然而，刘等人（2014）对该方案的安全性进行了重新评估，表明所提出的算法仅需一个已知明文图像即可被破解；此外，还指出了该加密方案在敏感性分析方面的其他局限性。埃尔‐利法特和牛（2013）设计了一种使用循环椭圆曲线和混沌系统的图像加密算法。使用一个256位的外部密钥和混沌系统生成初始密钥，接着将生成的密钥与来自循环椭圆曲线点的密钥结果相结合。但是，刘和刘（2014）使用一对明文图像/密文图像成功破解了该方案。

本文旨在提出一种具有结构简单和可变性特点的新型基于混沌的算法，我们引入了一种基于置乱‐扩散结构的可调彩色图像加密方案，该方案采用具有良好动态特性的分段非线性混沌映射。仅在一轮加密中即可获得令人满意的安全性能，并且与现有的彩色图像加密方案相比，渲染效果得到改善。实验结果表明，所提出的算法是安全且高效的。因此，每个像素的加密不仅依赖于明文像素，还依赖于所有其他像素。因此，明文图像中任意像素的微小变化都将产生完全不同的密文图像。此外，通过引入调整参数，同一密钥可以将同一明文图像加密为不同的密文图像。因此，所提出的方案能够有效抵抗已知/选择明文攻击。

本文其余部分安排如下：在第2节中，我们阐述了分段混沌系统；在第3节中，我们描述了所提方案；第4节给出了性能和安全性分析，结论部分设计在第5节。

2 分段线性混沌映射系统

分段线性混沌映射系统具有良好的遍历性，并且对初始值非常敏感，适用于密码学。分段线性混沌映射系统如公式(1)所示。

$$
F(x_i) =
\begin{cases}
p x_i, & 0 \leq x_i \leq p \
p - (x_i - p), & p \leq x_i \leq 0.5 \
1 - p(x_i - 0.5), & 0.5 \leq x_i \leq 1
\end{cases}
\quad (1)
$$

当 $ x \in [0, 1) $ 且控制参数 $ p \in (0.5, 0) $ 时，该映射是混沌的（Fouda 等，2014年）。

在本文中，该映射的一些初始值 $ x $ 和控制参数 $ p $ 被设为密钥的一部分。

在所提方案的置换和扩散过程中均使用了混沌分段线性混沌映射系统。在混淆阶段，我们通过以下方程将随机序列转换为整数序列：

$$
\alpha_i = \text{fix}(\text{bitsll}(x_i, 8)) \quad (2)
$$

其中，$ \text{fix}(n) $ 返回 $ n $ 的整数部分，$ \text{bitsll}(n, i) $ 返回输入操作数 $ n $ 按位左移 $ i $ 位后的值。

3 提出的图像加密方案

3.1 置换过程

为了消除相邻像素之间的相关性，使用分段线性混沌映射系统对明文图像的像素进行置换过程。此步骤中使用两个随机序列，以增强置换空间和方案的安全性。

设 $ I $ 为大小为 $ H \times W \times 3 $ 的明文彩色图像。该置换过程表达如下。

1. 使用密钥 $ (x_1, p_1) $ 和 $ (x_2, p_2) $ 两次迭代分段线性映射，得到两个长度均为 $ 3 \times H \times W/2 $ 的随机序列 $ {x’ 1, x’_2, …, x’ {3HW/2}} $, $ {x’‘ 1, x’‘_2, …, x’‘ {3HW/2}} $。
2. 将这两个序列的连续值交替赋值，构造一个新的序列 $ S = {x’ 1, x’‘_1, x’_2, x’‘_2, …, x’ {3HW/2}, x’‘_{3HW/2}} $。接着将 $ S $ 按升序排列，得到索引顺序序列 $ {O_i, i = 1,…,3 \times H \times W} $。
3. 将明文图像重塑为一个向量 $ U $；使用 $ O $ 对向量 $ U $ 进行打乱，得到打乱的向量 $ P $。

3.2 扩散过程

在所提出的方案中，每个密文像素不仅与生成它的明文像素相关，还与其他所有像素相关。因此，明文图像中任意像素的微小变化都会导致完全不同的密文图像。

此外，为了确保所提方案的可变性，已采用调整参数加密的概念。因此，在添加调整参数后，使用相同的密钥可以将同一明文图像加密为不同的密文图像。因此，调整参数的作用是提供可变性（利斯科夫等人，2011年）。

定义所提方案的扩散过程，该过程有三个输入：一个密钥 $ K \in {0, 1}^k $ （$ k $ 为密钥空间），一个调整参数 $ T \in {0, 1}^t $ （$ t = 256 \times 256 $），以及置乱向量 $ P \in {0, 1}^n $ （$ n = H \times W \times 3 $），并输出密文图像 $ C’ \in {0, 1}^n $。该函数在公式(3)中定义：

$$
\phi: {0,1}^k \times {0,1}^t \times {0,1}^n \rightarrow {0,1}^n \
(K, T, P) \rightarrow C’
\quad (3)
$$

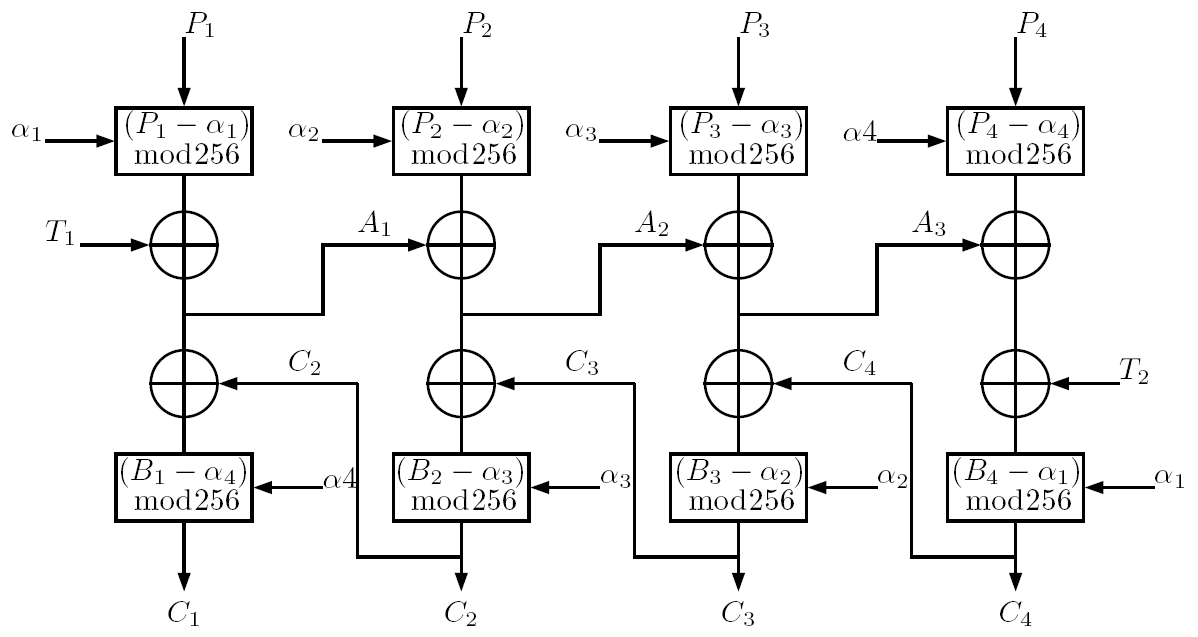
图1 展示了所提方案的扩散模型。所提出的扩散方法的算法解释详见算法1。

算法1 扩散

1. 输入：打乱向量：$ P $；密钥参数：$ x_3, p_3 $；调整参数：$ T_1, T_2 $；图像尺寸：$ H, W $
2. 输出：密文图像: $ C’ $
3. 使用 $ x_3, p_3 $ 通过公式(1)生成大小为 $ 3 \times H \times W $ 的混沌序列 $ X $
4. 将 $ X $ 转换为整数序列，即使用公式(2)得到 $ \alpha $
5. $ A_0 \leftarrow T_1 $
6. $ m \leftarrow 3 \times H \times W $
7. for $ i = 1 $ 到 $ m $ do
8. $ R_i \leftarrow (P_i - \alpha_i) \mod 256 $
9. $ A_i \leftarrow R_i \oplus A_{i-1} $
10. $ A_m \leftarrow A_m \oplus T_2 $
11. $ C_m \leftarrow (A_m - \alpha_1) \mod 256 $
12. for $ i = m - 1 $ 到 $ 1 $ 执行
    13. $ A_i \leftarrow A_i \oplus C_{i-1} $
    14. $ C_i \leftarrow (A_i - \alpha_{m-i+1}) \mod 256 $
13. 将得到的结果 $ C $ 重塑回三维矩阵，得到加密图像 $ C’ $
14. 返回 $ C $

4 提出的图像解密算法

4.1 逆扩散算法

所提出的可调整扩散机制的逆过程需要三个输入：密钥 $ K \in {0,1}^k $、调整参数 $ T \in {0,1}^t $ 和密文图像 $ C’ \in {0,1}^n $，并输出打乱后的向量 $ P \in {0,1}^n $。

逆扩散方法的算法解释详见算法2。

算法2 逆扩散

1. 输入：密文图像: $ C’ $; 密钥参数: $ x_3, p_3 $; 调整参数: $ T_1, T_2 $; 图像尺寸: $ H, W $
2. 输出：打乱向量: $ P $
3. 将加密图像 $ C’ $ 重塑为一个向量 $ C $
4. 使用 $ x_3, p_3 $ 通过公式(1)生成大小为 $ 3 \times H \times W $ 的混沌序列 $ X $
5. 将 $ X $ 转换为整数序列，即使用公式(2)得到 $ \alpha $
6. $ m \leftarrow 3 \times H \times W $
7. $ A_m \leftarrow (C_m + \alpha_1) \mod 256 $
8. $ A_m \leftarrow A_m \oplus T_2 $
9. for $ i = m - 1 $ 到 $ 1 $ 执行
10. $ A_i \leftarrow (C_i + \alpha_{m-i+1}) \mod 256 $
11. $ A_i \leftarrow A_i \oplus C_{i-1} $
12. $ A_0 \leftarrow T_1 $
13. for $ i = 1 $ 到 $ m $ 执行
14. $ R_i \leftarrow A_i \oplus A_{i-1} $
15. $ P_i \leftarrow (R_i + \alpha_i) \mod 256 $
16. 返回 $ P $

4.2 逆置换算法

1. 使用密钥 $ (x_1, p_1) $ 和 $ (x_2, p_2) $ 对分段线性映射进行两次迭代，得到两个长度均为 $ 3 \times H \times W/2 $ 的随机序列 $ {x’ 1, x’_2, …, x’ {3HW/2}} $, $ {x’‘ 1, x’‘_2, …, x’‘ {3HW/2}} $。
2. 将这两个序列的连续值交替组合，形成一个新的序列 $ S = {x’ 1, x’‘_1, x’_2, x’‘_2, …, x’ {3HW/2}, x’‘_{3HW/2}} $，然后将 $ S $ 按升序排列，得到索引顺序序列 $ {O_i, i = 1,…,3 \times H \times W} $。
3. 使用 $ O $ 对打乱的向量 $ P $ 进行逆置换，得到向量 $ U $。
4. 将向量 $ U $ 转换为原始彩色图像 $ I $。

5 性能分析

已进行数值模拟，以验证所提出的加密方案在不同安全措施下的性能。采用尺寸为 256 × 256 的标准彩色图像“Lena”、“Pepper”和“Boat”作为明文图像。设定的控制参数和初始值为：$ x_1 = 0.3425 $，$ x_2 = 0.7759 $，$ x_3 = 0.9286 $，$ p_1 = 0.4549 $，$ p_2 = 0.2543 $ 和 $ p_3 = 0.1974 $，调整参数设置为 $ T_1 = 174 $，$ T_2 = 210 $。仿真结果如图2所示。可以看出，明文图像分别显示在图2(a)、2(b)和2(c)中，而图2(d)、2(e)和2(f)分别为对应的加密图像。

Lena (b)pepper (c)boat (d)(e)(f)对应的密文图像)

5.1 密钥空间分析

一个密码系统的密钥空间应足够大，以确保其在面对暴力攻击时的安全性。在提出的图像加密算法中，密钥包括：
1. 控制参数 $ p_1, p_2, p_3 $
2. 初始值 $ x_1, x_2, x_3 $

对于分段线性混沌映射系统，其敏感性被视为 $ 10^{-16} $（刘和王，2011）。因此，每个初始值的密钥空间为 $ 10^{16} $。而控制参数 $ p_1, p_2, p_3 \in (0, 0.5) $，则每个控制参数的密钥空间为 $ 0.5 \times 10^{16} $。因此，所提方案的密钥空间为 $ 0.125 \times 10^{96} $。该密钥空间足够大，足以使任何密钥穷举攻击都不可行。

5.2 敏感性分析

5.2.1 差分攻击

一个好的加密算法应对明文图像的修改具有敏感性，因此明文图像中的微小变化应在密文图像中产生显著改变。为了评估单像素修改对密文图像的影响，通常使用两个指标：像素变化率（NPCR）和归一化平均变化强度（UACI），其定义可参考毛等人，2004：

$$
\text{NPCR} {R,G,B} = \frac{\sum {i,j} f_{R,G,B}(i,j)}{W \times H} \times 100\% \quad (4)
$$

$$
\text{UACI} {R,G,B} = \frac{1}{W \times H} \sum {i,j} \frac{|C_{R,G,B}(i,j) - \hat{C}_{R,G,B}(i,j)|}{255} \times 100\% \quad (5)
$$

其中 $ W $ 和 $ H $ 分别表示图像的宽度和高度。$ C_{R,G,B}(i,j) $ 是加密图像，而 $ \hat{C} {R,G,B}(i,j) $ 是明文图像的一个像素被改变后的加密图像。对于位置 $ (i,j) $ 处的像素，如果 $ C {R,G,B}(i,j) \neq \hat{C} {R,G,B}(i,j) $，则令 $ f {R,G,B}(i,j) = 1 $；否则令 $ f_{R,G,B}(i,j) = 0 $。

仅改变明文图像中随机选择的一个像素的最低位。使用不同的图像进行了 NPCR 和 UACI 测试，并重复实验 50 次。实验结果如表1所示。此外，与现有的彩色图像加密方案进行了比较，结果表明所提出的方案具有非常出色的性能。

算法	NPCR%			UACI%
	R	G	B	R	G	B
提出的	99.9281	99.8346	99.6896	33.5821	33.6687	33.5408
王和张（2015）	99.6124	99.6134	99.6192	33.4438	33.5232	33.5010
刘和卡迪尔（2015）	99.6231	99.6338	99.6170	33.4747	33.5683	33.3382
张和肖（2014）	99.6755	99.6622	99.6619	33.4216	33.4211	33.4308
穆里略‐埃斯科巴等人 (2015年)	99.63	99.60	99.61	33.31	33.34	33.43
卡迪尔等人 (2014年)	99.5643	99.6258	99.6285	35.4560	33.2199	33.0184

5.2.2 密钥敏感性分析

所有图像加密方案的通用条件是密钥敏感性。为了评估所提出算法的密钥敏感性，测试中使用了两个密钥。第一个密钥是原始密钥，而我们仅对其中一个参数进行了 $ 10^{-16} $ 的修改，其余参数保持不变。然后，使用这两个略微不同的密钥对明文图像 Lena 进行加密。

对两个加密图像进行了比较。结果汇总于表2，显示出所提方案具有很高的密钥敏感性。此外，如果对密钥进行微小修改，并使用修改后的密钥来解密密文图像，则解密将完全失败。图3展示了测试结果。

修改	NPCR%			UACI%
参数	R	G	B	R	G	B
$ p_1 $	99.5918	99.6235	99.6044	33.4980	33.4622	33.5187
$ p_2 $	99.6326	99.5975	99.6227	33.4481	33.4973	33.4648
$ p_3 $	99.6109	99.6349	99.6162	33.4513	33.5476	33.4739
$ x_1 $	99.6243	99.6033	99.6204	33.4405	33.4446	33.4838
$ x_2 $	99.6082	99.6254	99.5922	33.4800	33.4686	33.5027
$ x_3 $	99.6204	99.6120	99.6140	33.5223	33.5197	33.4917

原始Lena图像 (b)使用原始密钥生成的密文图像 (c)使用仅修改了p1的修改后的密钥生成的密文图像 (d)(b)与(c)之间的差异 (e)使用原始密钥解密得到的解密图像 (f)使用修改后的密钥解密得到的解密图像)

5.2.3 调整参数敏感性

另一方面，本节还研究了调整参数敏感性，以确保所提方案的可变性。为了评估调整参数敏感性，仅改变两个调整参数中其中一个的最低有效位，并使用相同的密钥和略有不同的调整参数对两个加密图像进行比较。表3显示了所提方案的调整参数敏感性评估。因此，所提方案对调整参数的更改非常敏感。

修改	NPCR%			UACI%
参数	R	G	B	R	G	B
$ T_1 $	99.5865	99.6170	99.6231	33.6509	33.5369	33.4196
$ T_2 $	99.6201	99.6094	99.5941	33.4452	33.5396	33.4855

5.3 加密图像的随机性特性

为了测试所提方案生成的加密图像的随机性，使用了NIST（2010）测试套件版本。由于该统计测试需要大量数据，测试中使用了512 × 512密文图像。结果的详细信息见表4，表明所有加密图像均成功通过了所有NIST测试。因此，采用所提出的方案得到的加密图像具有良好的随机性特性。

统计测试	测试图像
	Lena	Pepper	Boat
频率	0.753521	0.098943	0.157950
区块频率	0.322226	0.493783	0.427333
累积和（前向）	0.675485	0.093845	0.099758
累加和（逆向）	0.855466	0.077657	0.102114
Runs	0.193635	0.704893	0.225509
最长游程	0.825319	0.635556	0.347930
Rank	0.188150	0.785979	0.093579
FFT	0.354010	0.093089	0.797221
非重叠模板	0.014082	0.948289	0.704478
重叠模板	0.788155	0.950197	0.246692
通用统计	0.232503	0.980860	0.905970
近似熵	0.098851	0.001366	0.492156
随机游走	0.847058	0.439047	0.814918
随机游走变体	0.276227	0.675158	0.397392
序列1	0.146951	0.531820	0.096066
序列2	0.183719	0.755228	0.260585
线性复杂度	0.649625	0.038249	0.034130

5.4 统计分析

5.4.1 相关性分析

标准图像的相邻像素具有强相关性。一个良好的图像加密方案应消除这种相关性，以确保抵御统计分析的安全性。分别从明文图像“Lena”及其对应的密文图像的 R、G、B 分量中，随机选取水平、垂直和对角方向上各10,000对相邻像素，使用以下公式（Chen et al., 2004）计算每对像素的相关系数：

$$
r = \frac{\text{cov}(x,y)}{\sqrt{D(x)D(y)}} \quad (6)
$$

其中

$$
\text{cov}(x,y) = \frac{1}{N} \sum_{i=1}^{N} (x_i - E(x))(y_i - E(y)) \quad (7)
$$

$$
E(x) = \frac{1}{N} \sum_{i=1}^{N} x_i, \quad D(x) = \frac{1}{N} \sum_{i=1}^{N} (x_i - E(x))^2 \quad (8)
$$

表5 总结了使用所提方案获得的结果，并证明所提出的方案成功消除了相邻像素之间的相关性。此外，研究了原始图像和加密图像的相关系数，并与现有方案进行了比较。检验结果如表6所示。结果表明，明文图像中两个相邻像素的相关性接近1，而加密图像的相关性接近0。

方向	明文图像			密文图像
	R	G	B	R	G	B
水平	0.9680	0.9441	0.9179	0.0054	0.0027	0.0096
垂直	0.9516	0.9204	0.8955	0.0013	0.0104	0.0003
对角	0.9087	0.8729	0.8513	0.0027	0.0003	0.0047

算法	明文图像			密文图像
	水平	垂直	对角	水平	垂直	对角
提出的	0.9715	0.9478	0.9346	0.0007	0.0013	0.000001
王和张（2015）	0.9764	0.9546	0.9263	0.0098	0.0050	0.0013
董（2014）	0.9271	0.9230	0.9847	0.0058	0.0026	0.0024
刘等（2013）	0.9271	0.9230	0.9847	0.0580	0.0024	0.0170

5.4.2 直方图分析

直方图分析是评估图像加密方案强度的重要测试。图像直方图显示了图像中像素值的分布情况。从图4可以看出，三个加密图像的直方图相当均匀，攻击者无法通过直方图分析攻击提取任何信息。

Lena (b)Pepper (c)Boat)

5.5 熵分析

信息的一个主要随机性度量是信息熵。对于一个用N位编码的随机消息，理想的信息熵为8。因此，对于彩色加密图像，每个颜色通道的信息熵应接近8。信息熵计算公式为：

$$
H(m) = -\sum_{i=1}^{2^n} p(m_i) \log_2 p(m_i) \quad (9)
$$

表7表明，使用我们所提方法得到的密文图像在三个颜色通道上的熵值非常接近于8，且所提出的方案能够成功通过信息熵分析。

加密图像	分量
	R	G	B
Lena	7.9968	7.9973	7.9972
Pepper	7.9971	7.9973	7.9974
Boat	7.9974	7.9973	7.9974

5.6 选择明文攻击

在这种情况下，攻击者被设计为活跃的，并且可以访问预言机加密，能够加密任意选择的消息，但不能加密当前考虑的明文。

在所提方案中，一个像素的加密依赖于所有其他像素，并且每次加密都使用一个随机选择的调整参数；此外，如果对手尝试对同一明文图像进行两次加密，将得到两个不同的密文图像，因此所提出的方案是概率性的。

此外，所提方案在某种程度上呈现了一种加密的调整链模式，关于该模式在抵抗选择明文分析方面的安全性完整证明可在 Liskov 等人 (2011) 中找到。

6 结论

本文提出了一种基于使用调整参数的新彩色图像加密算法，以确保数字图像数据的保密性。仅通过一轮加密即可达到令人满意的安全性能，且与现有的彩色图像加密方案相比，有效性显著提高。通过使用多种安全措施进行了仿真和安全分析，所得结果证实了我们所提方案的有效性和安全性。