关于涉及频谱分辨率的一些问题以及FFT幅度谱数值矫正问题的梳理

本文纯原创，有不对的地方敬请指正，有不懂的地方可以讨论，搬运请注明来源，谢谢。

一、问题

在研究matlab的FFT函数的时候发现了如下问题：对于信号
$$y=e^{j2\pi f_{1}t}+e^{j2\pi f_{2}t}+e^{j2\pi f_{3}t}$$
其中$f_1=500Hz$，$f_2=505Hz$，$f_2=1010Hz$。当我用$F_s=5120Hz$的采样率对其进行采样得到512个离散数据点，画出其频谱为：

问题一：频谱本应该是在500Hz、505Hz和1010Hz三处有峰，但是频谱上却没有显示出505Hz的信号。
问题二：由时域表达式可知，三个不同频点的信号功率一致，都为1。但是幅度谱上却无体现。

二、频谱分辨率、栅栏效应及频谱泄露

在简介栅栏效应之前，我们要分清DTFT、DFT和FFT三者的关系，可以参考我的这篇文章。

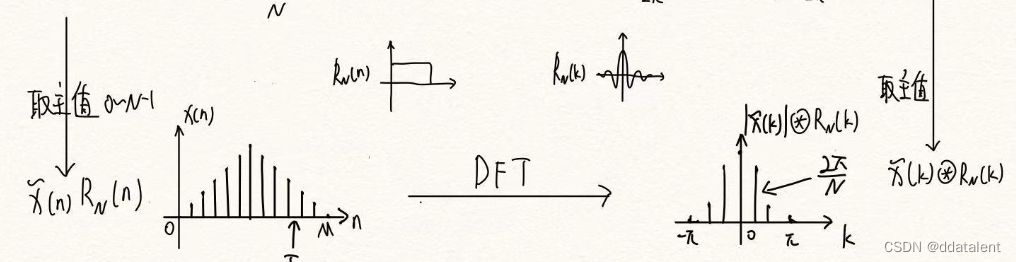
我们不妨细看DFT这个步骤，我们在matlab里调用FFT函数就是采用的DFT算法（当FFT点数是2的整数次幂的时候，就可以用快速傅里叶变换）。

2.1频谱分辨率

由上图可知，我们最终得到的时域信号是以采样周期$T=\frac{1}{Fs}$为间隔，频谱中的谱线以$\frac{2\pi }{N}$间隔，转换到数字上则有：$\Delta f=\frac{Fs}{N}$，在本例中频谱分辨率则是$\Delta f=\frac{5120}{512}=10Hz$。

2.2栅栏效应

我们可以想象，间隔10Hz的谱线，应该是会跳过我们的505Hz这个频点的信号。就好像通过栅栏观察频谱一样，因此叫做栅栏效应。

那么难道我们就观察不到这个频点的信号了吗？如果我们漏掉了505Hz这个频点的信号，那我们500Hz和1010Hz两个频点的信号功率不应该是一致的吗，怎么会幅度不一样呢？

2.3频谱泄露

由上图可知，DFT的最后一个步骤是加窗，将一个无限长的信号截断为有限长的信号。在频域上，就是卷积一个Sa函数。

Sa函数的特性是能量集中在主瓣，少部分能量分布在旁瓣。这样原本各个频点的冲激信号经过卷积变为了Sa函数，能量也从集中分布在某个频点变为大部分集中，小部分泄露的情况。这就是我们说的频谱泄露。

回归到这个例子中，505Hz频点处的信号能量理应集中分布在505Hz附近的主瓣中，少部分泄露到其他地方去了。

可是505Hz谱线最后由于频谱分辨率的原因并没有被采集到，而500Hz的谱线不仅集中了500Hz信号的能量，还因为离505Hz太近，包含在其主瓣内，分到了505Hz频点信号的能量，因此幅度变得特别大。而1010Hz离得很远，只分到了一点点的能量，所以它的幅度也不是整数。（具体该是多少我们下一章节讨论）

由此可见，如果需要缓解频谱泄露的问题，如何选择一个好的窗函数是很重要的。

2.4如何提高频谱分辨率

如要提高频谱分辨率，还是从公式考虑
$$\Delta f=\frac{Fs}{N}$$
要缩小$\Delta f$，采样率$Fs$一般是不做改动，而是增大$N$。通常大家会提到**“补零”、“重复数据”和“增加采样点”**三种方法，我们一一讨论

2.4.1补零是否可以提高分辨率？

频谱分辨率公式里的$N$究竟是什么呢？是采样点个数还是FFT点数？首先要分辨频谱密度和频谱分辨率两个不同的概念，经常有人对此混淆不清。
频谱密度=$\frac{Fs}{N_{fft}}$，$N_{fft}$是FFT点数。
频谱分辨率= F s m i n { N , N f f t } \frac{Fs}{min\{N,N_{fft}\}} min{N,Nfft​}Fs​，$N$是采样点个数。
我们讨论以下三种情况：

采样点个数=FFT点数

易知，当采样点个数与FFT点数相同时，频谱密度=频谱分辨率=$\frac{Fs}{N_{fft}}$=$\frac{Fs}{N}$。

采样点个数>FFT点数

当采样的数据点过多时候，如果做大点数的FFT变换，运算量会很大。一般会选择1024点，16384点这样的点数进行快速傅里叶变换以提高计算效率。
此时频谱密度=频谱分辨率=$\frac{Fs}{N_{fft}}$。但是增加FFT点数可以继续增大频谱分辨率，直到$\frac{Fs}{N}$为止，这也可以说是频谱分辨率的上限。

采样点个数< FFT点数

这就是我们常说的补0的情况。在这个例子中，我们用$F_s=5120Hz$的采样率对其进行采样得到512个离散数据点，结果没有分出500Hz和505Hz两个频点的信号。那我们在512个数据点后面补512个0，然后做1024点的FFT，这样频谱分辨率会不会变成5Hz，就可以区分出两个相邻频点的信号呢？

由上图可知，我们仍然无法区分出500Hz和505Hz两个相邻频点的信号，但是我们的谱线明显更平滑了。

其实，从数学的角度出发，我们可以知道，时域补0对应的是频域插值，插值只会让谱线更平滑，而不会引入新的频率分量。从公式的角度出发，增大了FFT的点数，频谱密度增大了，而频谱分辨率没有提升，因此还是无法区分相邻频点。

如果了解DFT和DTFT的关系就更容易理解， 补零越多，就是在DTFT连续的频谱上采样得到更密集的谱线而已。看我上面那个链接，再结合这篇文章可以很透彻的理解

但是补0也不是毫无作用的，此时看频谱的栅栏更密集了，更容易进行观察和分析。通常我们认为补0是无害的，可以适当补0以完成快速傅里叶变换。例如把500个点补到512个点进行FFT。

（题外话，时域插值是否可行）

既然时域补零对应频域插值，那时域插值对应的就是频域的补0，自然也无法引入新的频域分量。这是上采样的工作原理，有兴趣的可以看我这篇文章

2.4.2重复数据是否可以提高频谱分辨率

首先声明，本文不讨论周期信号进行整周期采样的情况。
一般来说我们采样得到的信号都是非周期的，不管是对无限长非周期信号的采样，还是对周期信号的截断采样。
回到我们的例子，我们我们用$F_s=5120Hz$的采样率对其进行采样得到512个离散数据点，然后把它重复一遍，拼凑得到1024个数据点进行FFT

可以看出，确实多了一个频率分量，区分出来两个相邻频点的信号了。这是因为重复一遍信号，相当于增加了实际有用信息的采样点个数，因此不仅可以缓解频谱泄露的问题，还可以增大频谱分辨率。此时的频谱分辨率$\Delta f=\frac{5120}{1024}=5Hz$。

不过这种方法也有缺点，它伪造了一个与实际信号可能并不相符的新的信号出来，这样得到的频谱与我们实际信号的频谱有所区别。只有当我们无法获取更多采样点的时候才考虑这种方法。

2.4.3增加采样点是否可以提高频谱分辨率

先说结论，这是唯一正确的方法。增加采样点个数相当于加窗的时候加了一个更长的窗，不仅有效缓解了频谱泄露的问题，也大大提升了频谱分辨率。只是很多时候受限于存储条件和计算性能的限制，我们无法采样得到足够多的数据点进行FFT变换。

回到我们的例子，我们我们用$F_s=5120Hz$的采样率对其进行采样得到1024个离散数据点进行FFT，此时的频谱分辨率$\Delta f=\frac{5120}{1024}=5Hz$。恰好可以分辨出500Hz和505Hz两个相邻频点信号。

而且此时频谱泄露的问题得到了有效缓解，各个频点的信号的功率没有泄漏到其他频点，所有频点信号的功率一致，幅度谱上都显示1024。

由此我们解决了问题一，那么问题二究竟是怎么回事呢？

三、FFT幅度谱数值矫正问题

我们重新来看我们的信号
$$y=e^{j2\pi f_{1}t}+e^{j2\pi f_{2}t}+e^{j2\pi f_{3}t}$$
这是由三个平均功率为1的复单音信号合并而成的一个混合信号。
我们对其采样1024点做1024点FFT，以及采样2048点做2048点FFT得到两个频谱。

我们看幅度，做1024点FFT的三根谱线的幅度都是1024，而做2048点FFT的三根谱线的幅度是2048。由帕萨瓦尔定理我们可知

信号在时域的总能量等于信号在频域的总能量，即信号经傅里叶变换后其总能量保持不变，符合能量守恒定律。

明明他们都是平均功率为1的信号啊，怎么会这样呢？我们还是要从FFT底层入手。

要知道，非周期信号FFT算的是傅里叶变换，周期信号FFT算的是傅里叶级数（因为周期信号傅里叶变换是$\delta$冲激函数，没有意义）

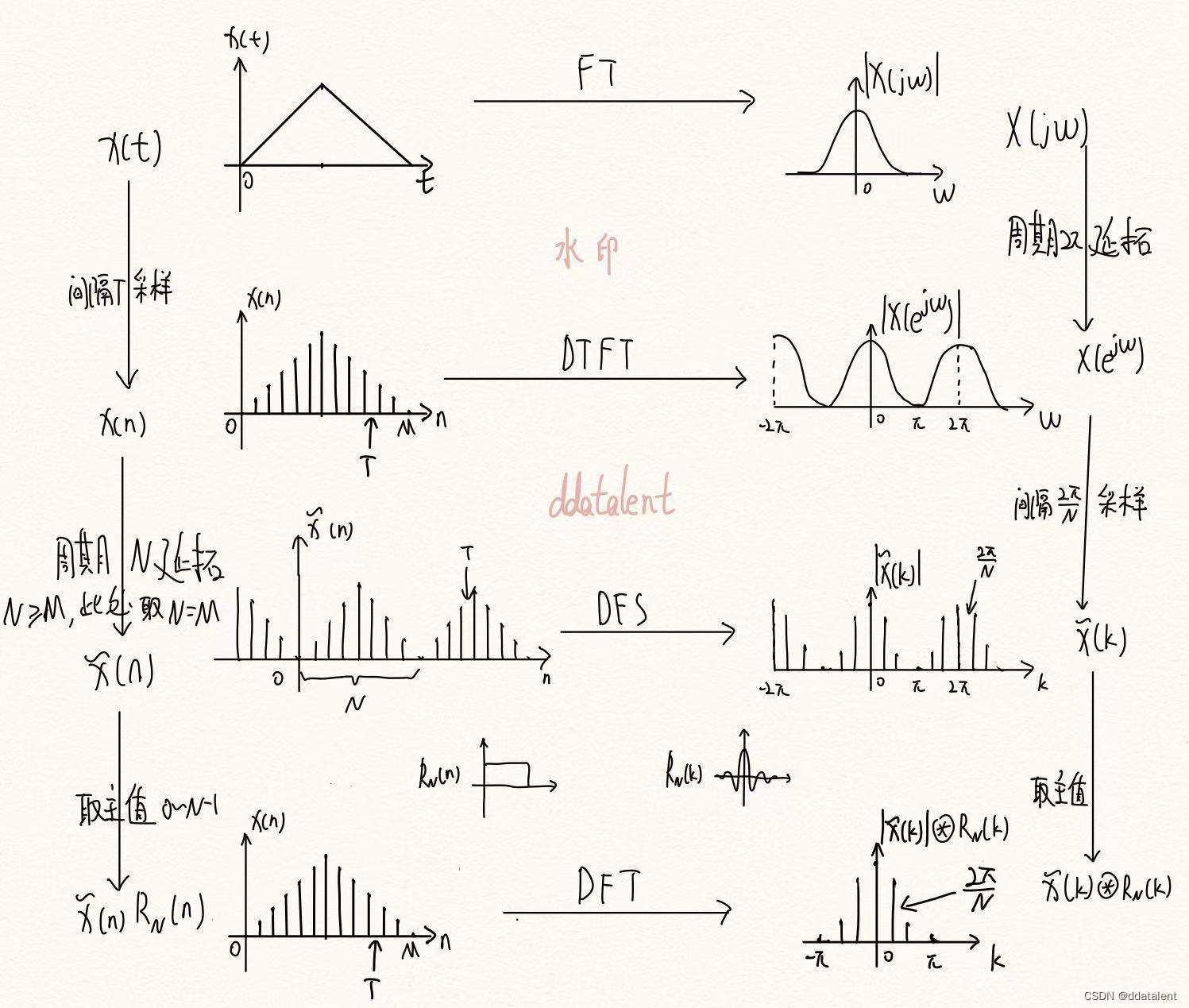
回到我最开始引用的那篇文章里的这个图，由于非周期无限长的信号没有办法求得离散频谱，因此我们是对其做一个周期延拓得到周期信号，然后求得离散频谱。

对一个周期延拓的信号，求的是其傅里叶级数。而我们本来要求的是非周期信号的傅里叶变换。那么DFS和DFT求得东西是一样的吗？

我们看公式：

离散周期傅里叶级数DFS
$$x[n]=\sum _{k=0}^{N-1}{a}_k{e}^{jk(2\pi /N)n}$$
$$a_k=\frac{1}{N}\sum _{n=0}^{N-1}x[n]e^{-jk(2\pi /N)n}$$
离散傅里叶变换DFT
$$x[n]=\frac{1}{N}\sum _{k=0}^{N-1}X[k]e^{jk(2\pi /N)kn}$$
$$X[k]=\sum _{n=0}^{N-1}x[n]e^{-jk(2\pi /N)kn}$$

仔细比较就可以发现，DFT算出来的X[k]的幅度是$a_k$的N倍，Matlab中FFT使用的就是这个算法，所以实际的幅值大小要乘以1/N。

回到我们的例子，我们在1024点FFT频谱中得到的幅度是1024，乘以1/N得到1，所以各频点信号的平均功率为1，与时域功率一致，符合帕萨瓦尔定理。

但是为什么有的文章说要乘以2/N那？这只是单边谱和双边谱的区别，DFT算出来的是双边谱，换算到单边谱幅度要加倍，注意直流不加倍，仅此而已。

在进行谱分析的过程中我们其实一般不会注意到幅度具体的值，只会关注该点有无信号以及信号强度相对大小，但是若能够了解其幅度变换关系，相信更有利于大家的分析！