如何理解注意机制中经常提到的键、查询和值 ?

Attention 机制很厉害，但是他是怎么想出来的，少有人讨论。stackexchange 上有人讨论了一些，可作为参考：

neural networks - What exactly are keys, queries, and values in attention mechanisms? - Cross Validated

置顶的回答：

键/值/查询的概念类似于检索系统。例如，当您在Youtube上搜索视频时，搜索引擎会将您的查询(搜索栏中的文本)映射到数据库中与候选视频相关的一组键(视频标题、描述等)，然后向您显示最佳匹配的视频(值)。

注意操作也可以被认为是一个检索过程。

接下来这个回答解释了注意力机制的好处：

在seq2seq模型中，我们将输入序列编码为上下文向量，然后将该上下文向量提供给解码器以产生预期的良好输出。

但是，如果输入序列很长，只依赖一个上下文向量就不那么有效了。我们需要输入序列(编码器)中隐藏状态的所有信息来进行更好的解码(注意机制)。

一种利用输入隐藏状态的方法如下所示:

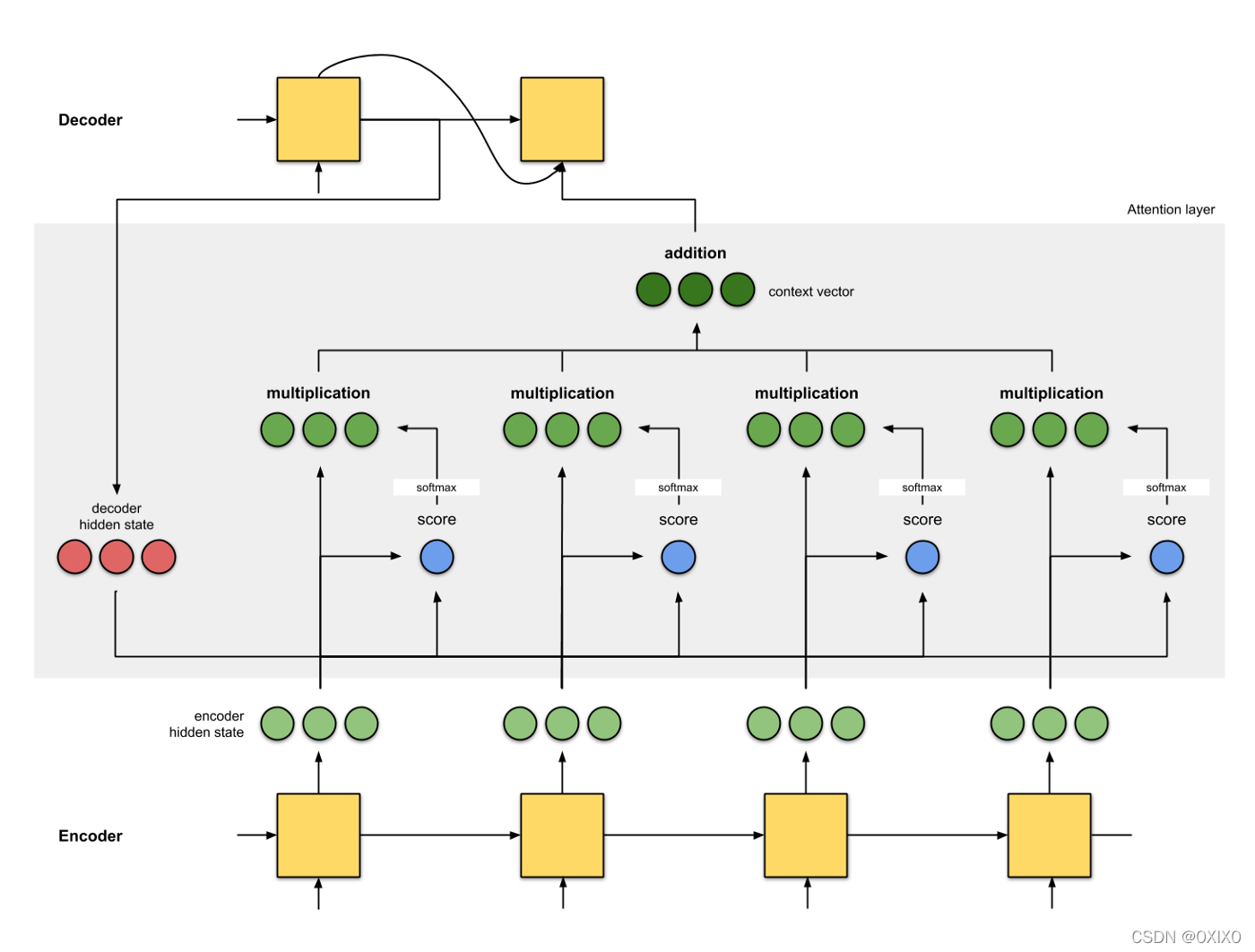
换句话说，在这种注意机制中，上下文向量是作为值的加权和计算的，其中分配给每个值的权重是通过与相应键的查询的兼容函数计算的(这是来自 [Attention Is All You Need]的一个稍微修改过的句子)

这里，查询来自解码器的隐藏状态，键和值来自编码器的隐藏状态(键和值在此图中是相同的)。分数是查询和键之间的相似性，它可以是查询和键之间的点积(或其他形式的相似性)。然后，这些分数通过softmax函数生成一组权重，其总和等于1。每个权值乘以它对应的值，得到上下文向量，它利用所有的输入隐藏状态。

请注意，如果我们手动将最后一个输入的权重设置为1，其所有优先级设置为0，那么我们将注意机制减少到原始的seq2seq上下文向量机制。也就是说，不需要注意先前的输入编码器状态。

现在，让我们考虑如下图所示的自我注意机制:

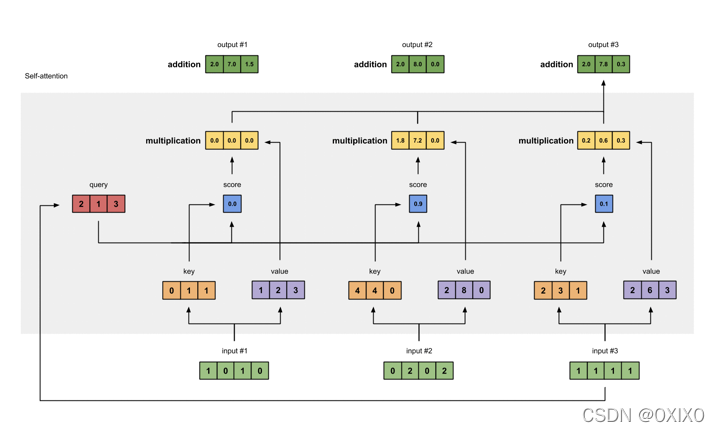
与上图的不同之处在于，查询、键和值是对应输入状态向量的转换。其他的保持不变。

注意，我们仍然可以使用原始的编码器状态向量作为查询、键和值。那么，我们为什么需要这种转变呢?这个变换是一个简单的矩阵乘法，像这样:

Query = I x W(Q)

Key = I x W(K)

Value = I x W(V)

其中I是输入(编码器)状态向量，W(Q)、W(K)和W(V)是将I向量转换为Query、Key、Value向量的相应矩阵。

这个矩阵乘法(向量变换)的好处是什么?

显而易见的原因是，如果我们不转换输入向量，用于计算每个输入值的权值的点积将总是为单个输入token本身产生最大的权值得分。这可能不是我们想要的情况，例如，对于代词标记，我们需要它注意它的所指物。

另一个不太明显但重要的原因是，转换可能会为Query、Key和Value产生更好的表示。回想一下奇异值分解(SVD)的效果，如下图所示:

通过将一个输入向量与一个矩阵V(来自SVD)相乘，如果这两个向量在主题空间中类似，如图中示例所示，我们可以获得计算两个向量之间兼容性的更好表示。

这些用于变换的矩阵可以在神经网络中学习!

简而言之，将输入向量与矩阵相乘，得到:

1、增加每个输入token处理输入序列中其他tokens的可能性，而不是单个token本身。

2、可能是输入向量更好的(潜)表示;

3、将输入向量转换为一个具有期望维数的空间，例如，从维数5到维数2，或从维数n到m，等等(这实际上很有用);

注意转换矩阵是可学习的(不需要手动设置)。

我希望这能帮助您理解深度神经网络(自我)注意机制中的查询、键和值。

我的思考：

从之前 seq2seq 的注意力机制可以看出一些 transformer 中注意力机智的雏形。transformer的作者可能在考虑语言理解问题的时候重点考虑了 it 这类词的指代问题。因为 word2vec 得到的词向量，类似词语的距离已经是接近的了。所以不需要很特别的机制，就可以计算一句话里那些词可能是关联的。对于 it 指代这个问题，它和YouTube检索太像了，作者可能就产生了联想。这样将一个词分为 Q、K、V  三个向量就多了一个存储关系的空间。下图是一个答主的示意，也可以做参考：

 文末顺带给有道翻译点赞！本文都是用“有道翻译”翻译的，翻译文本基本可以直接使用。论文这种专业文本都翻译这么好，很厉害。