上一篇博客提到 K-kmeans 算法存在好几个缺陷,其中之一就是该算法无法聚类哪些非凸的数据集,也就是说,K-means 聚类的形状一般只能是球状的,不能推广到任意的形状。本文介绍一种基于密度的聚类方法,可以聚类任意的形状。
基于密度的聚类是根据样本的密度分布来进行聚类。通常情况下,密度聚类从样本密度的角度出来,来考查样本之间的可连接性,并基于可连接样本不断扩展聚类簇,以获得最终的聚类结果。其中最著名的算法就是 DBSCAN 算法
DBSCAN 算法有两个参数:半径 eps 和密度阈值 MinPts,具体步骤为:
1、以每一个数据点 xi 为圆心,以 eps 为半径画一个圆圈。这个圆圈被称为 xi 的 eps 邻域
2、对这个圆圈内包含的点进行计数。如果一个圆圈里面的点的数目超过了密度阈值 MinPts,那么将该圆圈的圆心记为核心点,又称核心对象。如果某个点的 eps 邻域内点的个数小于密度阈值但是落在核心点的邻域内,则称该点为边界点。既不是核心点也不是边界点的点,就是噪声点。
3、核心点 xi 的 eps 邻域内的所有的点,都是 xi 的直接密度直达。如果 xj 由 xi 密度直达,xk 由 xj 密度直达。。。xn 由 xk 密度直达,那么,xn 由 xi 密度可达。这个性质说明了由密度直达的传递性,可以推导出密度可达。
4、如果对于 xk,使 xi 和 xj 都可以由 xk 密度可达,那么,就称 xi 和 xj 密度相连。将密度相连的点连接在一起,就形成了我们的聚类簇。
用更通俗易懂的话描述就是如果一个点的 eps 邻域内的点的总数小于阈值,那么该点就是低密度点。如果大于阈值,就是低密度点。如果一个高密度点在另外一个高密度点的邻域内,就直接把这两个高密度点相连,这是核心点。如果一个低密度点在高密度点的邻域内,就将低密度点连在距离它最近的高密度点上,这是边界点。不在任何高密度点的 eps 邻域内的低密度点,就是异常点。
周志华《机器学习》书上给的伪代码如下。

公式性有点强,用语义表达算法的伪码如下:
|
1、根据 eps 邻域和密度阈值 MinPts ,判断一个点是核心点、边界点或者离群点。并将离群点删除
2、如果核心点之间的距离小于 MinPts ,就将两个核心点连接在一起。这样就形成了若干组簇
3、将边界点分配到距离它最近的核心点范围内
4、形成最终的聚类结果 |
DBSCAN 算法评价及改进
DBSCAN优点:
1、对噪声不敏感。这是因为该算法能够较好地判断离群点,并且即使错判离群点,对最终的聚类结果也没什么影响
2、能发现任意形状的簇。这是因为DBSCAN 是靠不断连接邻域呢高密度点来发现簇的,只需要定义邻域大小和密度阈值,因此可以发现不同形状,不同大小的簇
DBSCAN 缺点:
1、对两个参数的设置敏感,即圈的半径 eps 、阈值 MinPts。
2、DBSCAN 使用固定的参数识别聚类。显然,当聚类的稀疏程度不同,聚类效果也有很大不同。即数据密度不均匀时,很难使用该算法
3、如果数据样本集越大,收敛时间越长。此时可以使用 KD 树优化
Python 代码:
from sklearn.datasets.samples_generator import make_circles
import matplotlib.pyplot as plt
import time
from sklearn.cluster import KMeans
from sklearn.cluster import DBSCAN
X,y_true = make_circles(n_samples=1000,noise=0.15) #这是一个圆环形状的
plt.scatter(X[:,0],X[:,1],c=y_true)
plt.show()
#DBSCAN 算法
t0 = time.time()
dbscan = DBSCAN(eps=.1,min_samples=6).fit(X) # 该算法对应的两个参数
t = time.time()-t0
plt.scatter(X[:, 0], X[:, 1], c=dbscan.labels_)
plt.title('time : %f'%t)
plt.show()
初始数据点分布是这样的:
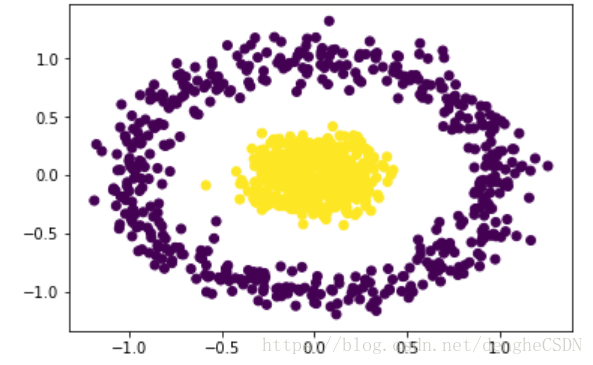
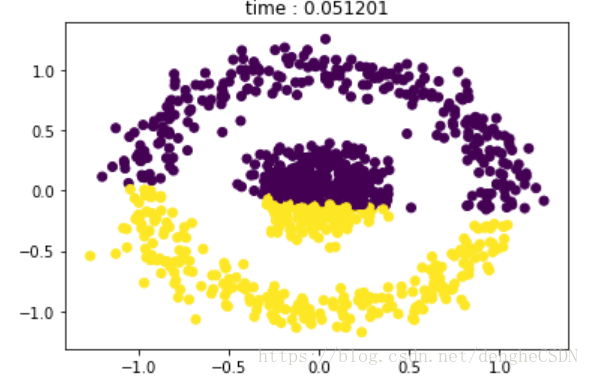
密度阈值均取 6,eps 分别为 0.01,0.05,0.2,0.8时的聚类效果
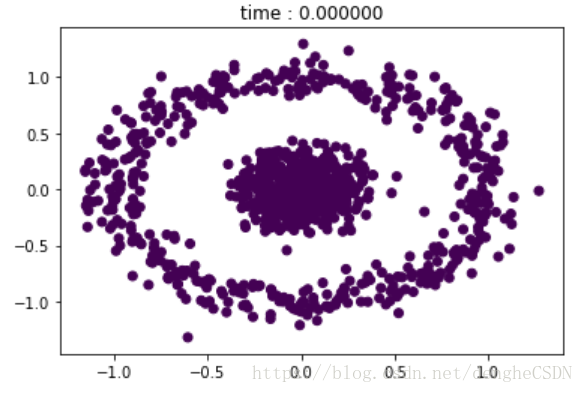
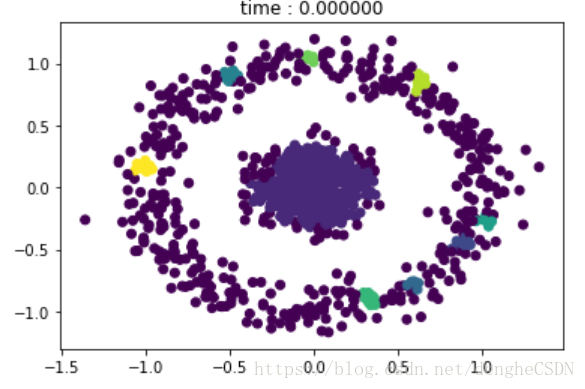
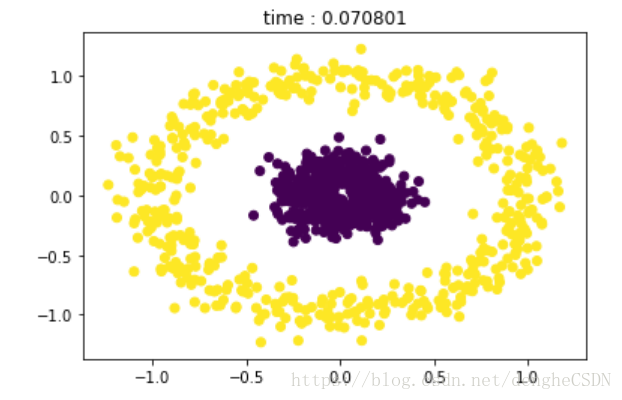
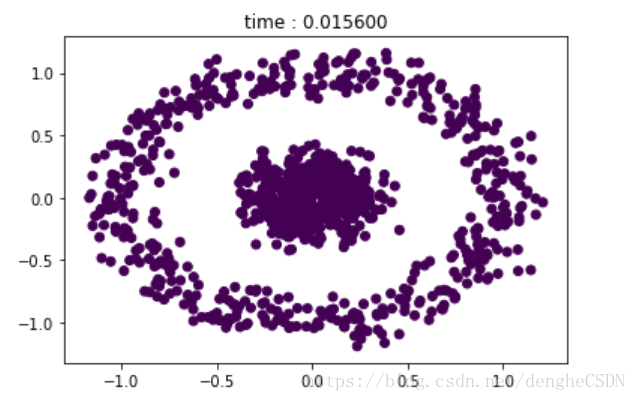
来来来,你再看看 K-means 的聚类效果,对于非凸的数据聚类效果就是这个样子。。。
 du
du
拓展阅读:
1、为了解决 DBSCAN 很难聚类不同密度的簇,目前已经有很多新的方法被发明出来,比如OPTICS(Ordering points to identify the clustering structure)将邻域点按照密度大小进行排序,再用可视化的方法来发现不同密度的簇
2、2014年Science杂志刊登了一种基于密度峰值的算法DP(Clustering by fast search and find of density peaks),也是采用可视化的方法来帮助查找不同密度的簇。其思想为每个簇都有个最大密度点为簇中心,每个簇中心都吸引并连接其周围密度较低的点,且不同的簇中心点都相对较远。为实现这个思想,它首先计算每个点的密度大小(也是数多少点在邻域eps-neigbourhood内),然后再计算每个点到其最近的且比它密度高的点的距离。这样对每个点我们都有两个属性值,一个是其本身密度值,一个是其到比它密度高的最近点的距离值。对这两个属性我们可以生成一个2维图表(决策图),那么在右上角的几个点就可以代表不同的簇的中心了,即密度高且离其他簇中心较远。然后我们可以把其他的点逐步连接到离其最近的且比它密度高的点,直到最后连到某个簇中心点为止。这样所有共享一个簇中心的点都属于一个簇,而离其他点较远且密度很低的点就是异常点了。由于这个方法是基于相对距离和相对密度来连接点的,所以其可以发现不同密度的簇。DP的缺陷就在于每个簇必须有个最大密度点作为簇中心点,如果一个簇的密度分布均与或者一个簇有多个密度高的点,其就会把某些簇分开成几个子簇。另外DP需要用户指定有多少个簇,在实际操作的时候需要不断尝试调整。
话说,一个聚类算法就可以发 Science 了吗????哪位大佬帮我解释下





 本文介绍了基于密度的聚类算法DBSCAN,详细阐述了DBSCAN算法的工作原理、参数设置、优缺点,并通过Python代码展示了不同eps值下的聚类效果。此外,还探讨了DBSCAN在数据密度不均匀时的挑战以及相应的优化方法,如OPTICS和DP算法。
本文介绍了基于密度的聚类算法DBSCAN,详细阐述了DBSCAN算法的工作原理、参数设置、优缺点,并通过Python代码展示了不同eps值下的聚类效果。此外,还探讨了DBSCAN在数据密度不均匀时的挑战以及相应的优化方法,如OPTICS和DP算法。
















 2554
2554










