逻辑回归算法是用于分类的。本案例中,建立一个逻辑回归模型来预测一个学生是否被大学录取。假设你是一个大学系的管理员,你想根据两次考试的结果来决定每个申请人的录取机会。你有以前的申请人的历史数据,你可以用它作为逻辑回归的训练集。对于每一个培训例子,你有两个考试的申请人的分数和录取决定。为了做到这一点,我们将建立一个分类模型,根据考试成绩估计入学概率。
1、首先,导入库,并且读取数据集。原来数据集是 .txt 结尾的。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import os
path = 'LogiReg_data.txt'
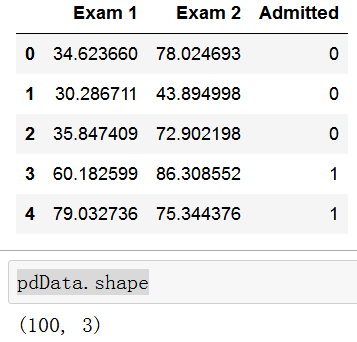
pdData = pd.read_csv(path, header=None, names=['Exam 1', 'Exam 2', 'Admitted'])由于原始数据中并没有给出每一列的列的名字,所以,我们自己加一个 “Exam 1”、"“Exam 2”、"Admitted",我们最好列举前几行数据,确认一下是否读入了数据,并且,看一下数据的维度:
pdData.head()
pdData.shape显示结果如下:
2、将数据分成正负样本,利用散点图,大致看一下数据分布(不是必要步骤,而且因为数据只有两个维度,才添加了此步骤)
positive = pdData[pdData['Admitted'] == 1]
negative = pdData[pdData['Admitted'] == 0]
fig, ax = plt.subplots(figsize=(10,5))
ax.scatter(positive['Exam 1'], positive['Exam 2'], s=30, c='b', marker='o', label='Admitted')
ax.scatter(negative['Exam 1'], negative['Exam 2'], s=30, c='r', marker='x', label='Not Admitted')
ax.legend()
ax.set_xlabel('Exam 1 Score')
ax.set_ylabel('Exam 2 Score')补充说明一下:Admitted 是标签,当标签为 1 时,认为是正样本;标签为 0 时,认为是负样本。而 pd Data['Admitted'] == 1,是一堆 True 和 false。散点








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 825
825

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








