@TOC最简单的单纯形法是用来解决形如
min /max cx
Ax <= b
x>=0
这样的问题的，那么如何解决呢，我觉得这篇知乎上的帖子写的很好，直接搬运过来了：
我们直接给出线性规划的标准型：
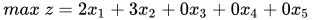
①初始基可行解的确定：先写出系数矩阵为
,(非负条件不写在内)可见这个矩阵是53维的，根据上一节所讲的知识我们需要找一个33维的非奇异子矩阵，观察到他的后三列列向量是相互独立的，可以构成一组基，即为
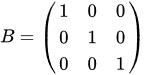②求出基可行解
,B所对应的基变量分别是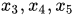
。这时在约束条件上进行变换，把基变量分别表示出来
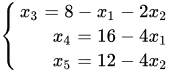,此时基变量表达式带入目标函数之中有：
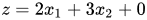（目标函数之中基变量的系数均为零），此时我们只改变非基变量，就可以得到不同的基可行解。如当令
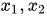均等于0时，z＝0。此时就得到了一个基可行解X. 
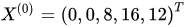。这个基可行解的实际意义是有利润的产品1，2均未被生产，故利润也为0。这一个基可行解对应的顶点处无法取到最优解。所以我们要换下一个顶点找。我们可以通过分析解析式来推出顶点需要怎么换。
③最优性检验
我们看目标函数的表达式：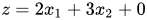
，非基变量的系数为正，表示只要非基变量增加，z也会增加，代表z并没有达到最优解。同时这样系数为正的表达式并无法反应出约束条件对z的影响，所以我们要想办法去换元，使变量的系数都为负，然后式子中的那个常数就为最优解。
④换基变量
顺着这个思路我们来对我们的式子变换，我们先选择正系数最大的变量 ，把它转换为其他变量。我们称 当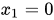 
，有
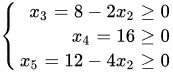，由非负条件，我们换基时也要保证变量≥0 。所以
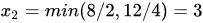此时
均满足非负条件。此时 为换出基变量。所以现在我们要做的事情就是把所有的 换为 。输入基变量换为输出基变量。
原有式子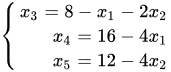
做简单的变换
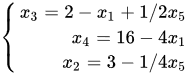就达到了互换的目的。下一步再做最优性检测，将上式带入到目标函数中得到：
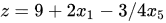发现还是存在正系数 ，说明还不是最优解。我们需要再进行一次迭代。
⑤迭代运算
显然换入基变量 为x1,x2,x3 时，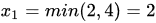
,所以换出基变量为 x3 。作变换有
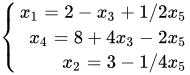，得到基可行解 
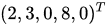,带入目标函数发现仍然有正系数，继续进行迭代得出基可行解 
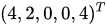，此时的目标函数为
。
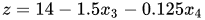终于！我们得到了一个想要的函数表达形式。所以最优解就为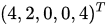
，对应z的最大值为14
从这里之后大家大概就对单纯形法有了一定的了解，但如果大家看运筹学教材或者从其他方面了解单纯形法就会发现，他们的解释形式不是这样的，又时候会列一些表，有时候会摆出一堆数字，还有一些类似于检验数的概念。（另外说一句，单纯形表之类的可能和上面方程组的差不多，有时间可以去体会一下。）
为什么呢，从我的理解来说，一开始人们想出这个单纯形法的时候应该是按如上的方法列方程组一步一步做的。但随着对处理大量数据的需要，即线性代数以及相关知识方面的拓展，（大家都知道现在方程组都是以矩阵的形式表示的，而对其计算方法属于线性代数），而且我们发现在所有的迭代过程中，方程组都是以第一个等式所演变的矩阵等式Ax=b所表示的,而且我们现在有了线性代数的计算知识，为什么不能把所有量都以一开始所给的量为基准进行一些变换演变过来呢。当然这只是一个猜测，不过事实证明确实可以，而且也确实是这么做了
从计算机的角度来说，如果我们按照手写方程组的方式贮存每一步迭代的数据，那么相比于只存下第一步的数据，明显是耗费过多的，在数据量大的时候尤为明显。所以我们学习单纯形法普遍以只存下第一步数据，再对其进行矩阵形式变换表示迭代的每一个过程的每一组数据为准，而一般不怎么说如上方程组的形式。
以上都是我根据我对单纯形认识的说法，并不专业。
以下是一个例题的计算步骤与单纯形法matlab代码
如果这里有一些部分不理解为什么会这样做，建议把第一部分的方程组和这里的直接给出的数据结合起来就会知道给出的特定的如z之类的数据是什么意思，至于具体证明，如果非要想知道的，我这里大概也说不明白了，建议去网上找一些书籍，因为我也只是个实用派，而且我并不是学习这方面的，只是因为要用才学了一下，希望理解。
function [M,x,minf] = SimpleMthd(A,c,b,baseVector)
diedaicishu = 0;
sz = size(A); %生成矩阵【A矩阵的行数，列数】
nVia = sz(2); %约束矩阵的列数,或者说费用向量的维数,此题为2
n = sz(1); %约束矩阵的行数，此题为3
xx = 1:nVia;
nobase = zeros(1,1); %生成 1*1的 0矩阵
m = 1;
for i=1:nVia
if(isempty(find(baseVector == xx(i),1)))
nobase(m) =i; %找到i，如果为0，停止
m = m+1; %产生nobase[1,2]
else
;
end
end
bCon = 1;
M = 0;
while bCon
nB = A(:,nobase); %非基变量矩阵
ncb = c(nobase); %非基变量系数
B = A(:,baseVector);%基变量矩阵
cb = c(baseVector);%基变量系数
xb = inv(B)*b; %这三个参数都是计算中的常用部分，
f = cb*xb;
w = cb*inv(B);
for i=1:length(nobase) %sigma 判别数，理解为基变量前面的系数
sigma(i) = w*nB(:,i)-ncb(i); %在矩阵变换中表示为
end %cb*inv(B)*nB-ncb 意义为（正号，表示下降速度，个人理解）
[maxs,ind] = max(sigma); %找出判别数中最大的那个，记录下标为ind，这就是所需要的出基变量
if maxs <= 0 %如果都小于0，这就是最优解，输出结果
minf = cb*xb;
vr = find(c~=0,1,'last'); %最后一个系数不为0的变量的下标
for l=1:vr
ele = find(baseVector ==1,1);%找出baseVector为l的数的下标
if(isempty(ele))
x(l) = 0;%如果为0，为0
else
x(1) = xb(ele);%不为0，输出
end
end
bCon = 0; %结束标志
else
y=inv(B)*A(:,nobase(ind)); %被选中的基变量前的系数
if y <= 0 %如果都小于0，那么该问题无界，无最优解
disp('不存在最优解！');
x = NaN;
minf = NaN;
return;
else
minb = inf; %先设minb为无穷大
chagB = 0; %chagB 记录下标的参数
for j=1:length(y)
if y(j)>0
bz = xb(j)/y(j);
if bz<minb
minb = bz;
chagB = j; %对y中每一个进行寻找，如果xb（j）/y(j)大于0，且最小
end %那么为所需要的入基变量
end
end
tmp = baseVector(chagB);
baseVector(chagB) = nobase(ind);
nobase(ind) = tmp; %将基变量放入基变量的（下标）数组中，非基变量放入非基变量（下标）数组中
%baseVector由[3 4 5]变成了[3 4 1],;另一个[1 2]》》[5 2]
end
end
M=M+1;
if (M == 1000000)
disp('找不到最优解！');
x = NaN;
minf = NaN;
return;
end
end注释的某些部分不是很专业。。
当然其实matlab自带的优化函数更方便而且高效，这里写出来只是加深大家对这个的理解。
测试用例：
A = [-1 2 1 0 0;2 3 0 1 0;1 -1 0 0 1];
c = [-4 -1 0 0 0];
b = [4;12;3];
[x mf] = SimpleMthd(A,c,b,[3 4 5]);
那么如果问题变复杂了我们的小于号变成了大于号呢。
解释一下为什么大于号小于号会造成差别
面对小于号与b大于0时我们会发现（0，0，0，0，0，0，0……)必定是原方程的一个解，称为初始可行解，（了解之前的知识就会发现，之前的问题都是预选000为初始解的，因为这是最简单，最容易找到的解），那么如果情况改变了，出现了大于号，（000）不在范围内呢，那么就需要我们自己去找迭代的第一步的解了。
那么这里引入了二阶段法和大M法。
@TOC二阶段法
在引入松弛变量（不知道什么是松弛变量的可以去自己找一下，之前没写这个，主要是没注意，而且这个也很简单）使不等式变成等式之后，再引入人工变量（人工变量在这里都大于0，引入的原则是使形成单位矩阵，便于计算），再求1人工变量的和（你用10也可以），如果求出来人工变量都是0的话那么就得到了初始解。就可以代入原式进行正常的单纯形法了。
@[TOC](3.大M法：)大M法：
大M法原理类似于 1对于无穷大来说和0差不多。这里依旧是引入人工变量。如果得到的解中，人工变量不是全为0的话，该问题无解，解出来全为0的话所得就是最终解。
上面的几种方法写的只是针对最小化问题，其实最大化问题也差不多，修改一些细节即可。
@TOC修正单纯形法：
我们前面说明了把方程组里加过来减过去的形式转化为各个特定部分组成的矩阵乘积形式，这样可以简化计算，而且步骤看起来非常格式化，每一步都是去找特定的值，然后判断，选取，迭代，结束，非常适合编程。
但以计算机计算的角度来说，这样真的好吗，问题比较简单的时候或许差不多，但我们计算的时候会发现一个关键就是 B^-1,这个东西是求每一步迭代中的特定值时所必须要求的，如果我们引入了六七个松弛变量，那么这就变成了六七阶的矩阵求逆，而且每一次迭代都要求一次，计算量非常大，考试的时候总是只让你求三四阶的随机矩阵逆就是这个原因，对于电脑来说也是一样的。
所以提出了修正单纯形法对其进行了折中，从粗略上看可能像是方程组解题和线性代数解题的结合版，会让人疑问为什么会提出这样一个不伦不类的解法，但精华在于通过多储存了一些数据解决了B^-1的求取问题，减少了一定的计算量，这在解决大规模问题时是十分关键的。
function [x,minf] = ModifSimpleMthd(A ,c ,b,baseVector)
sz = size(A);
nVia = sz(2);
n = sz(1);
xx = 1:nVia;
nobase = zeros(1,1);
m = 1;
if c >= 0
vr = find(c ~= 0,1,'last');
rgv = inv(A(:,(nVia-n+1):nVia))*b;
if rgv >= 0
x = zeros(1,vr);
minf = 0;
else
disp('不存在最优解！');
x = NaN;
minf = NaN;
return;
end
end
for i=1:nVia
if(isempty(find(baseVector == xx(i),1)))
nobase(m) =i; %找到i，如果为0，停止
m = m+1;
else
;
end
end
bCon = 1;
M = 0;
B = A(:,baseVector);
invB = inv(B);
while bCon
nB = A(:,nobase);
ncb = c(nobase);
B = A(:,baseVector);
cb = c(baseVector);
xb = invB*b;
f = cb*xb;
w = cb*invB;
for i=1:length(nobase)
sigma(i) = w*nB(:,i)-ncb(i);
end
[maxs,ind] = max(sigma);
if maxs <= 0
minf = cb*xb;
vr = find(c~=0,1,'last');
for l=1:vr
ele = find(baseVector ==l,1);
if(isempty(ele))
x(l) = 0;
else
x(l) = xb(ele);
end
end
bCon = 0;
else
y=inv(B)*A(:,nobase(ind));
if y <= 0
disp('不存在最优解！');
x = NaN;
minf = NaN;
return;
else
minb = inf;
chagB = 0;
for j=1:length(y)
if y(j)>0
bz = xb(j)/y(j);
if bz<minb
minb = bz;
chagB = j;
end
end
end
tmp = baseVector(chagB);
baseVector(chagB) = nobase(ind);
nobase(ind) = tmp;
for j = 1:chagB-1
if y(j) ~= 0
invB(j,:) = invB(j,:) - invB(chagB,:)*y(j)/y(chagB);
end
end
for j = chagB+1:length(y)
if y(j)~= 0
invB(j,:) = invB(j,:) - invB(chagB,:)*y(j)/y(chagB);
end
end
invB(chagB,:) = invB(chagB,:)/y(chagB);
end
end
M = M + 1;
if (M == 1000000)
disp('找不到最优解！');
x = NaN;
minf = NaN;
return;
end
end测试用例：
A=[2 -1 1 0 0;2 1 0 -1 0;1 2 0 0 1];
c = [1 -3 1 0 0];
b = [8;2;10];
[x,mf]=MOdifSimpleMthd(A,c,b,[3 4 5])
@TOC5.对偶单纯形法：
首先什么是对偶这里就粗略提一下了，再线性规划里，一般就是根据原问题的每一个区块作出判断将其逆转到另一个区块所形成的一个新问题叫做它的对偶问题。
如：
明显注意到min和max，c和b的位置互换了等等。以及补充一条性质，如果原问题解出来有极大值（极小值），那么这也是对偶问题的极小值（极大值）
在引入的松弛变量为负系数但又不想引入人工变量的时候可以使用这种方法，
类比于原来的单纯形法，你需要保持判别数小于0（极小值问题），同时不断把b由负数变成正数，因为在这里b和判别数的意义在其对偶问题里已经互换了，这样是为了保证在对偶问题里的递增与可行性，最后如果有解，那么它就是原，对偶问题共同的解。
因为实力和时间都有点不够的情况，这篇博文里应该是会有点问题的，而且有点虎头蛇尾，希望理解，欢迎指正
2309
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
