修正单纯性算法、对偶问题及理论与对偶单纯型算法

参考来源运筹学与控制论

一、修正单纯性算法

1.1 修正单纯性算法基本思想与优势

修正单纯形算法的基本思想就是在给定一个初始可行基矩阵 𝑩 的逆矩阵以及初始基本可行解之后，通过不断地修正旧的可行基矩阵的逆矩阵 𝑩−1，获得新的可行基矩阵的逆矩阵 𝑩̂−1，进而完成单纯形算法所需要的其他运算。在迭代过程中，修正单纯形算法只保留一些重要的核心信息，其他的信息可以根据需求适时地生成出来，因而可以节省内存空间。

1.2 算法基本流程

从上述修正单纯形算法中我们可以看出最耗费计算量的步骤是 step 1，在 step 1 中我们需要求解一个线性代数方程组。
$w=c_b{B}^{-1}$
那么关键就在于如何得到基矩阵的逆$B^{-1}$.一般来说直接求解$B^{-1}$需要$O(n^3)$的复杂度。但是在修正单纯形法中，我们发现前后两次迭代过程中的基矩阵只差别一列，利用这个性质我们可以实现对 $B^{-1}$的快速求解。
设基矩阵为：
$$B=(a_{j_1},a_{j_2},...,a_{j_m})$$
我们不妨设非基列$a_q$代替$B$的第$p$列$a_{j_p}$得到新的基为：

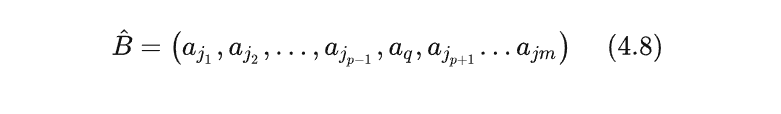
我们在上一步已经知道了$B^{-1}$，而现在需要求的是新的基矩阵的逆$\hat{B}$以转入下一次迭代。
这样的进基和出基操作相当于用 $m\ast m$初等矩阵：

左乘单纯形表的前m行。该矩阵可由单位矩阵经同样的初等变换得到。显然，它完全由 ${\bar{a}}_q$确定，除第 列外等同于一个单位阵。由 (4.8) 和 (4.9) 可推出：

至此，我们通过做一次矩阵乘法就可以得到${\hat{B}}^{-1}$,而不必直接求${\hat{B}}^{-1}$，这样就达到了节省计算量的目的，这也就是我们修正单纯形法的核心之处。

1.3 算法复杂度讨论

1.4 编写程序解决

参考修正单纯形算法bySunglary

二、对偶问题以及理论

2.1 从 reduced cost 出发导出线性规划对偶问题

如果是以往接触过线性规划的同学，或多或少肯定接触过对偶问题。那么头一次接触到对偶问题的时候，总会感觉到对偶问题出现地非常突兀，往往是不知道为什么就来突然要定义出一个对偶问题。那么本小节就从 reduced cost 的角度出发给出线性规划对偶问题一个从直觉上的观察。

首先回归线性规划的标准形式：

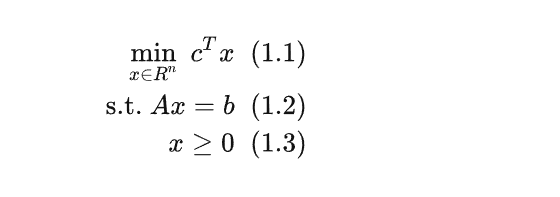
那么对上述线性规划问题，它的 reduced cost 的计算：
$$r_q=c_q-c_B^T{B}^{-1}{A}_q(1.4)$$
从之前的内容我们知道$r_q$代表着目标函数下降与否的，这是在单纯型算法中一个非常重要的指标。如果对于所有的$q$都有$r_q$那么我们就知道当前所在的点就是最优点，这一个结论在之前我们已经说明过了，如下所示：
定理一
若满足




线性规划问题(1.11-1.13) 就是线性规划问题(1.1-1.3)的对偶问题，简便起见我们也把(1.11-1.13)称之为对偶问题，把(1.1-1.3)称之为原问题。实际上在线性规划问题中是互为对偶的，但是在很多时候我们可能会刻意强调一方是另外一方的对偶，而忽略掉互为对偶。关于互为对偶的问题我们将在后边再详细讨论，此处不做展开了。

2.2 基于拉格朗日推导对偶问题

首先我们将原线性规划问题(1.1-1.3)中的约束，通过乘子的方式加入到目标函数中，即可得到松弛问题：


上述问题和我们上一节中给出的对偶问题是完全一样的。

基于拉格朗日松弛可以非常容易地推导出线性规划的对偶问题，并且我们从拉格朗日松弛的推导过程中可以获得关于对偶问题的一个直观的感受就是：对偶问题实际上是在寻找原问题（若是极小化问题）下界的最大值。采用拉格朗日来推导对偶问题的好处是你无需强行记忆线性规划对偶问题，而且在非线性规划中拉格朗日松弛的过程依然适用。

2.3 对偶问题和原问题的关系

2.3.1 弱对偶定理

若 $x4是原问题(1.1-1.3)的可行解，$w$是对偶问题 (1.11-1.13) 的可行解，则有 $c^{T}x>=b^{T}w$

从弱对偶定理出发，我们很快就可以得到三个非常重要的推论

推论1：若$x^0$是原问题 (1.1-1.3) 的可行解，$w^0$是对偶问题 (1.11-1.13) 的可行解，同时还有$c^T{x}^0=b^T{w}^0$成立，则表明 $x^0$是原问题的最优解，$w^0$是对偶问题的最优解。

证明：从弱对偶定理可得，对于任意的原问题可行解$x$有如下表达式成立$c^T{x}^0>=b^T{w}^0$ ，结合题目中条件进一步可得: $c^T{x}^0>=b^T{w}^0=c^T{x}^0$, 由上式可得$x^0$是原问题的最优解。证明 是对偶问题最优解的过程和上面的流程类似。

推论2 :若原问题最优解趋于负无穷，则对偶问题必不可行。

转化为逆否命题：若对偶问题有可行解，则原问题最优解必然有解。我们只需证明推论2上述的逆否命题即可。

推论3 ：若对偶问题最优解趋于正无穷，则原问题必然不可行。

还是转化为逆否命题：若原问题存在可行解，则对偶问题最优解必然有界。我们只需证明推论3上述的逆否命题即可。

2.3.2 强对偶定理

1、若原问题和对偶问题中有任意一个存在有界的最优解，则另外一个存在相同的最优解。

2、若原问题和对偶问题中有任意的最优解趋于无穷大，则另外一个不存在可行解。

2.4 对偶变量的物理意义----影子价格

这是一个在教材上被广泛使用的解释：如果原问题是企业A拥有m种资源（有m个约束），计划生产n种产品（有n个变量），目标是最大化总收入；那么对偶问题就是，企业B想要收购这些资源，需要确定m种资源的报价（有m个变量），目标是最小化总成本，但企业A只有在卖资源的收益不低于卖产品的时候才会同意卖资源（n个约束）。

企业A生产书架、桌子和椅子三种产品，拥有48单位木材，20单位塑料，8单位钢材三项资源。已知：书架售价60元，生产一个书架需要8单位木材、4单位制造塑料和2单位钢材；桌子售价30元，生产一张桌子需要6单位木材、2单位塑料和1.5单位钢材；椅子售价20元，生产一把椅子需要1单位木材、1.5单位塑料和0.5单位钢材；


如果企业B想要收购木材、塑料和钢材三种资源，就必须为每项资源报价，并且这个报价要让企业A愿意让出资源给企业B，即让企业A获得不低于自己制作产品的收入。设$y_1,y_2,y_3$分别为单位木材、塑料和钢材的报价。

由此可以写出对偶问题的线性规划为：

由此可以看出，对偶变量具备非常直观的物理含义，这种意义在经济学中体现的尤为明显。

三、对偶单纯型法

3.1 对偶单纯型法

我们根据强对偶定理可知，线性规划问题的原问题和对偶问题是等价的。这就自然而然让我们产生一个想法就是我们可以通过求解对偶问题来达到求解原问题的目的。我们从一个直观的例子先入手来看一下

之前我们在推导线性规划对偶问题的时候提到过，对偶问题决策变量的维数等于原问题约束的个数，那么确实从上面例子中我们可以发现原问题决策变量 $x$是四维的，而对偶问题决策变量 $w$是二维的。这就给了我们一个直观的启发，如果说线性规划的原问题的决策变量维数很多，而约束很少的话，我们把它转化为对偶问题后会得到一个约束很多，但是决策变量维数很少的对偶问题。这样转化之后，我们求解对偶问题可能会比求解原问题要简单。

以上仅仅是一个直观的想法，下面我们将这个直观的想法转化为具体的算法流程：



在对偶单纯形中有两个地方和原始单纯形有着很大的区别：

1、是进基的时候对偶单纯形选择的是$x_{j_p}<0$ 的非基变量，而不是选择 reduced cost 小于等于0的。
2、判断收敛性条件的时候，对偶单纯形中是检验解是否是可行的 $x_b>=0$
我们会在下一节最优性条件中再次分析一下原始单纯形和对偶单纯形的区别。

3.2 线性规划最优性条件

最优性条件对于优化问题而言往往有着举足轻重的作用。比方说通过最优性条件我们可以比较方便的验证一个可行解是不是最优解。本节我们集中讨论线性规划的最优性条件。

3.2.1 互补松弛条件

3.2.2 线性规划的KKT最优性条件

由此线性规划KKT条件的含义为：

1、需要原问题可行
2、需要对偶问题可行
3、原问题最优解和对偶问题最优解相等

实际上在原单纯形法中，我们是从满足 primal feasibility 的点但不满足 dual feasibility的点， 去逐渐搜索得到满足 dual feasibility 的点，最后使得使得 primal feasibility 和 dual feasibility 条件都满足，即得到最优解。

而在对偶单纯形法中，我们是从满足 dual feasibility 的点但不满足 primal feasibility 的点， 去逐渐搜索得到满足 prima feasibility 的点，最后使得使得 dual feasibility 和 primal feasibility 条件都满足，即得到最优解。

3.2.3 能否直接强解最优性条件？

到这里我们会产生一个念头就是我们是不是可以直接求解最优性条件来解线性规划问题呢？

事实上，直接求解最优性条件（也就是解KKT条件得到的方程组）确实可以用来求解线性规划问题，但是这么做并不会让问题变得简单。这是因为我们可以看出在最优性条件中 primal feasibility 和 dual feasibility 两个方程是线性代数方程，求解起来比较容易。而最后一个互补松弛条件 是一个多元二次方程组，求解起来比较困难。因此我们一般极少采用强解最优性条件的方法来解线性规划。