机器学习笔记—支持向量机（3）

线性不可分的线性支持向量机的学习问题为如下的凸二次规划问题（原始问题）：

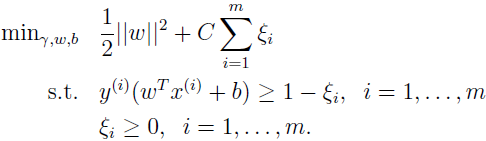
这是个凸二次规划问题，所以关于 {w,b,ξ} 的解释存在的。可以证明 w 的解是唯一的，但 b 的解不唯一，存在于一个区间。

设该问题的解是 w*、b*，于是得到分离超平面 w*·x+b*=0 及分类决策函数 f(x)=sign(w*·x+b*)。

构建拉格朗日函数：

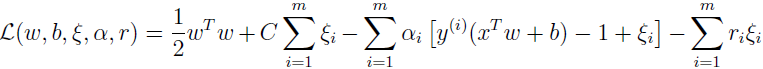其中 α_i 和 r_i 是拉格朗日乘子。

根据拉格朗日对偶性，原始问题的对偶问题是极大极小问题：

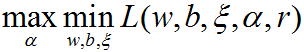
所以，为了得到对偶问题的解，需要先求 L(w,b,ξ,α,r) 对 w,b,ξ 的极小，由

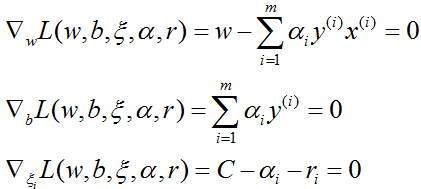
得

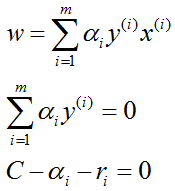
将上式代入拉格朗日函数，得

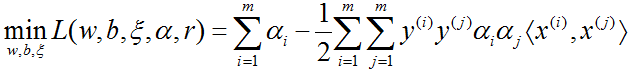
再对 min L(w,b,ξ,α,r)  求 α 的极大，即得对偶问题：

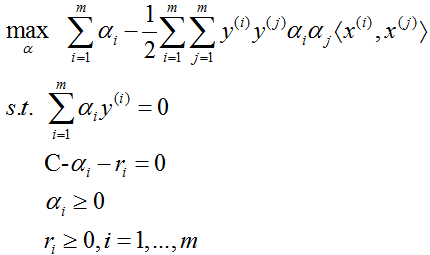
将上面的对偶最优化问题进行变换：利用等式约束消去 r_i，从而只留下变量 α_i，再将对目标函数求极大转换为求极小，于是得对偶问题：

可以通过求解对偶问题而得到原始问题的解，进而确定分离超平面和决策函数。 

设 α*=(α₁*,α₂*,...,α_m*) 是对偶问题的一个解，若存在 α* 的一个分量 α_j* ，0<α_j*<C，则原始问题的解 w*,b* 可按下式求得

于是得到分离超平面 w*·x+b*=0 及分类决策函数 f(x)=sign(w*·x+b*)。

下面我们就来讲如何解对偶问题。

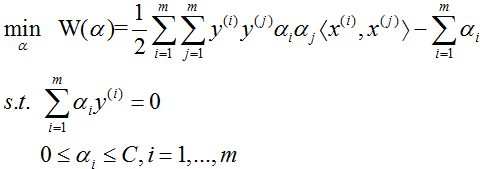
在对偶问题中，变量是拉格朗日乘子，一个变量 α_i 对应于一个样本点 (x_i,y_j)；变量的总数等于训练样本容量 m。

对偶问题也就是凸二次规划问题，凸二次规划具有全局最优解，有许多最优化算法可以用于解该问题，但是当训练样本容量很大时，这些算法往往变得非常低效，以致无法使用。所以，如何高效地实现支持向量机的学习就成为一个重要的问题。目前人们已提出许多快速实现算法。下面讲其中的序列最小最优化（sequential minimal optimization，SMO）算法，这种算法是 1998 年由 Platt 提出的。

SMO 算法是一种启发式算法，基本思路是：如果所有变量的解都满足此最优化问题的 KKT 条件，那么这个最优化问题的解就得到了。否则，选两个变量，固定其它变量，针对这两个变量构建一个二次规划问题，这个二次规划问题关于这两个变量的解应该更接近原始二次规划问题的解，因为这会使得原始二次规划问题的目标函数值变得更小。重要的是，这时子问题可以通过解析方法求解，这样就可以大大提高整个算法的计算速度。子问题有两个变量，一个是违反 KKT 条件最严重的那一个，另一个由约束条件自动确定。如此，SMO 算法将原问题不断分解为子问题并对子问题求解，进而达到求解原问题的目的。

注意，子问题的两个变量中只有一个是自由变量，假设 α_1,α₂ 为两个变量，α₁,α₂,…,α_m 固定，那么由等式约束 ∑α_iy_i=0 可知

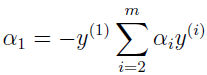
此处用到了 y∈{-1,1}。

如果 α₂ 确定，那么 α₁ 也随之确定。所以子问题中同时更新两个变量。

不失一般性，假设选择的两个变量是 α₁ 和 α₂，其它变量 α_i(i=3,4,...,m) 固定。于是对偶问题的子问题可以写成：

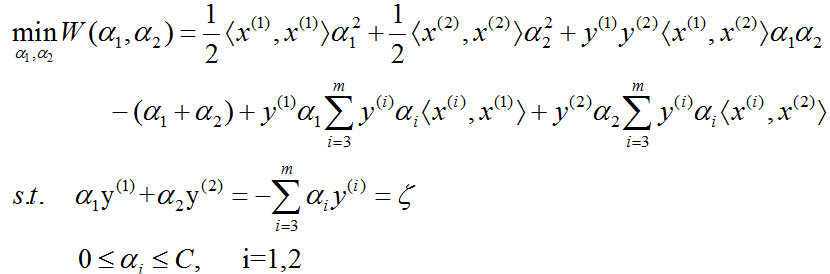
为表示方便起见，我们使用核函数 K_ij 来代替 〈x⁽ⁱ⁾,x^(j)〉，则上式就变成：

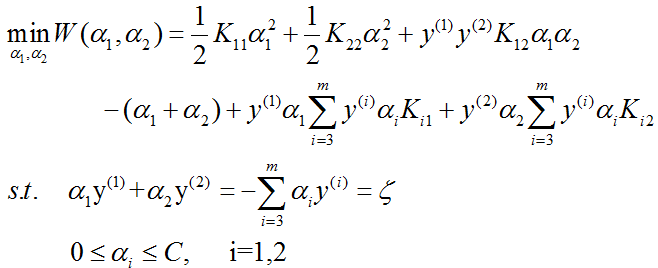
由 α₁y⁽¹⁾=ζ-α₂y⁽²⁾ 及 y_i²=1，可将 α₁ 表示成

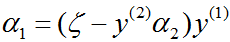
把 α₁ 代入 W(α₁,α₂)，得到只是 α₂ 的函数的目标函数：

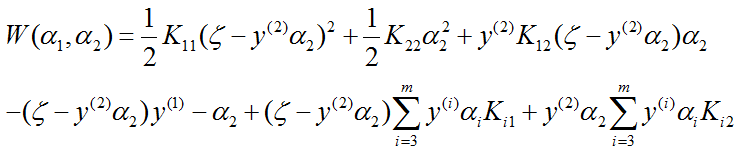
对 α₂ 求导数（自己手算下，再整理出结果）

令其为 0，得到

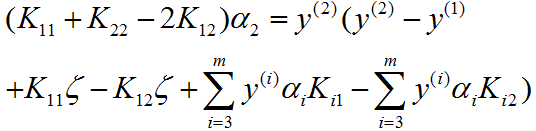
可得

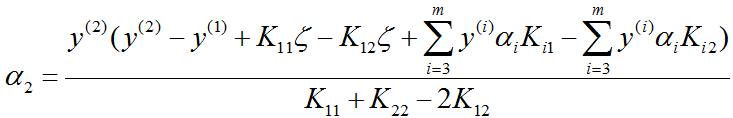
注意此处的 α₂ 是新值，且未经约束条件 α₁y⁽¹⁾+α₂y⁽²⁾=ζ 和 0≤α_i≤C ,i=1,2 的剪辑。

为避免混淆，我们把旧的 α₁ 和 α₂ 表示为 α_1^old 和 α_2^old，把上式等号左边的 α₂，也就是未经剪辑的 α₂ 表示为 α₂^new,unc，把剪辑后的 α₂ 表示为 α₂^new。

同时，把 ζ=α₁y⁽¹⁾+α₂y⁽²⁾ 代入上式得

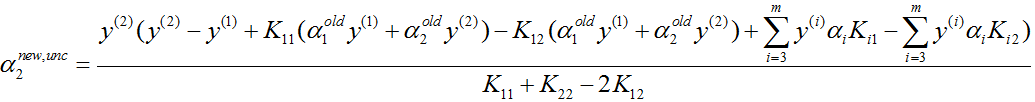
再经过约束条件 α₁y⁽¹⁾+α₂y⁽²⁾=ζ 和 0≤α_i≤C ,i=1,2 的剪辑，即可得解 (α_1^new,α_2^new)。

 

 

 

参考资料：

1、http://cs229.stanford.edu/notes/cs229-notes3.pdf

2、李航,著.统计学习方法[M]. 清华大学出版社, 2012

转载于:https://www.cnblogs.com/NaughtyBaby/p/5343883.html