【leetcode】01背包总结（2024/2/2更新）

本文内容参考了代码随想录，并进行了自己的总结。

01 背包

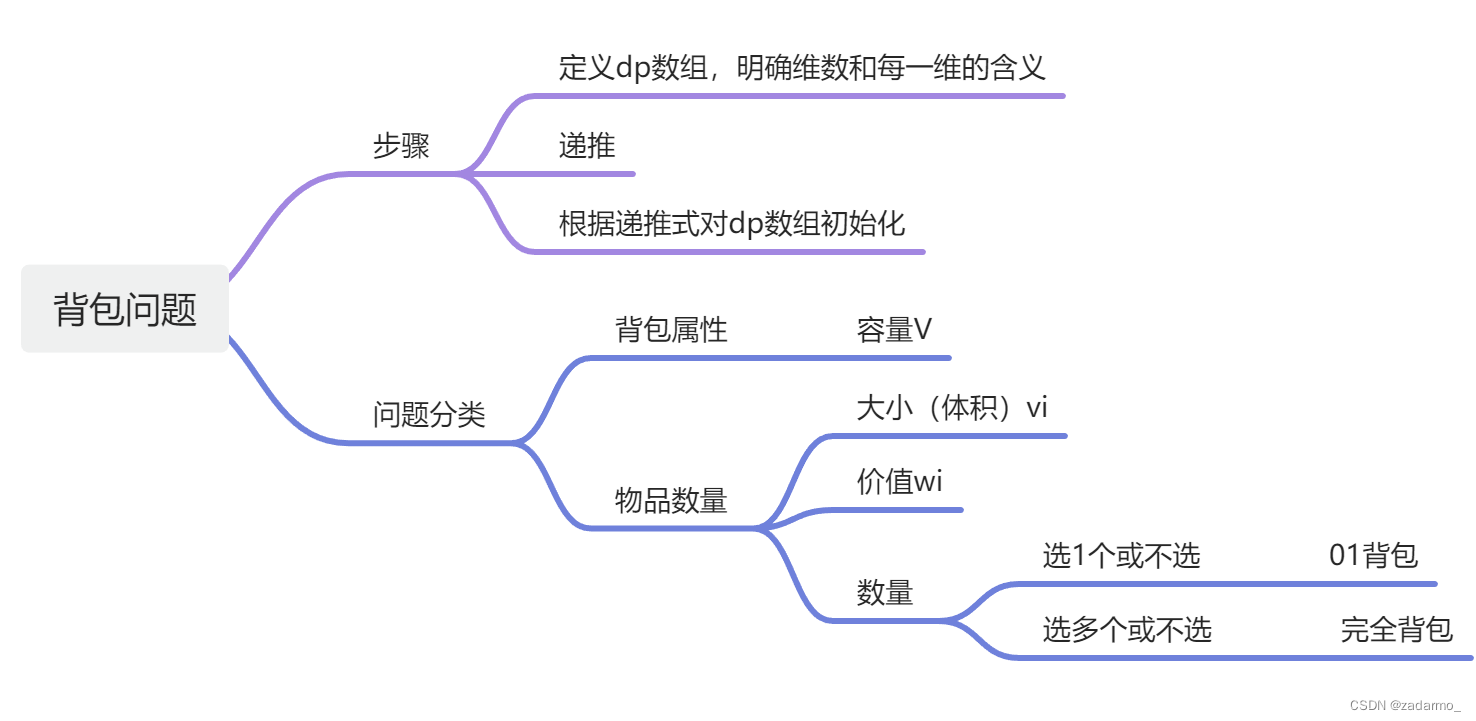
这篇文章先总结01背包，完全背包见下一篇文章。

关键点

• 每件物品只有两种状态：不选、选 1 件

代码

int N, W; // N件物品，容量为W
int w[N], v[N]; // w为大小，v为容量

/* 数组定义 */
int[][] dp = new int[N][W + 1]; // 注意是W + 1, 因为重量会取到W
dp[i][j]; // 从下标为[0, i]的物品中选若干件物品（注意是若干件，不是全部），放入大小为j的容器时的最大价值

/* 递推公式 */
// 由于每件物品有选、不选两种状态，所以两种状态取最大值即可
// 比如，对于dp[i][j]来说，
// 如果不选下标为i的物品，那么价值 = dp[i - 1][j]；
// 如果选下标为i的物品，那么价值 = dp[i - 1][j - w[i]] + v[i]
// 两种状态取max
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);

/* 初始化 */
// 从递推公式可以看出来，会存在dp[0][j]、dp[i][0]
// 对于dp[0][j]来说，回到数组定义，即选择下标为0的物品，放入大小为j的容器时的最大价值
// 这里又分两种情况，下标为0的物品的大小w[0]比j大，即放不进去，那么dp[0][j]=0；w[0]比j小，即放的进去，那么dp[0][j]=v[0]
// 对于dp[i][0]来说，回到数组定义，即从下标为[0, i]的物品中选若干件物品，放入大小为0的容器时的最大价值
// 显然dp[i][0] = 0
for(int i = 0; i < N; i ++ ) dp[i][0] = 0;
for(int j = 0; j <= W; j ++ ) {
	if (j >= w[0]) dp[0][j] = v[0];
    else dp[0][j] = 0;
}

/* 求解 */
// 先遍历物品、再遍历大小
// 由于dp[0]j]已经初始化过了，所以从第1件物品开始循环
// 由于dp[i][0]已经初始化过了，所以从重量为1开始循环
for(int i = 1; i < N; i ++ )
	for(int j = 1; j <= W; j ++ ) {
    	if (j < w[i]) dp[i][j] = dp[i - 1][j];
        else dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i];
    }

/* 输出答案 */
// dp[N - 1][W]: 即从[0, N-1]中选若干件物品，放入大小为W的容器时的最大价值
return dp[N - 1][W]; 

时间复杂度：O(NW)
空间复杂度：O(NW)

优化：滚动数组，二维空间 -> 一维空间

递推公式

滚动数组思想：
回到递推公式：
$dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-w[i]]+v[i])$

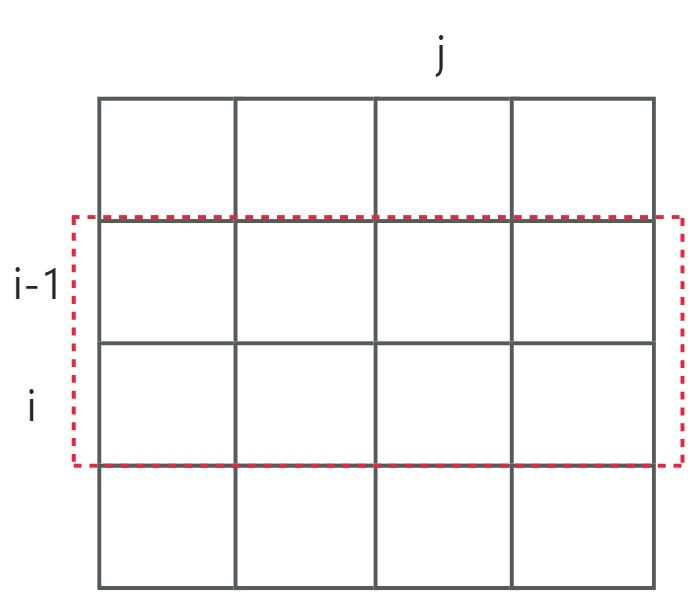
可以看出，第一维只用到了相邻两层的一个状态，没有第三个状态了。那实际上这个维度就可以去掉了，相当于用一个变量表示两个状态，赋值前就是上一层的状态，赋值后就是下一层的状态！
所以递推公式变成：
$dp[j]=Math.max(dp[j],dp[j-w[i]]+v[i])$

容量 W 遍历方向

对于遍历方向也需要改。如下图所示：

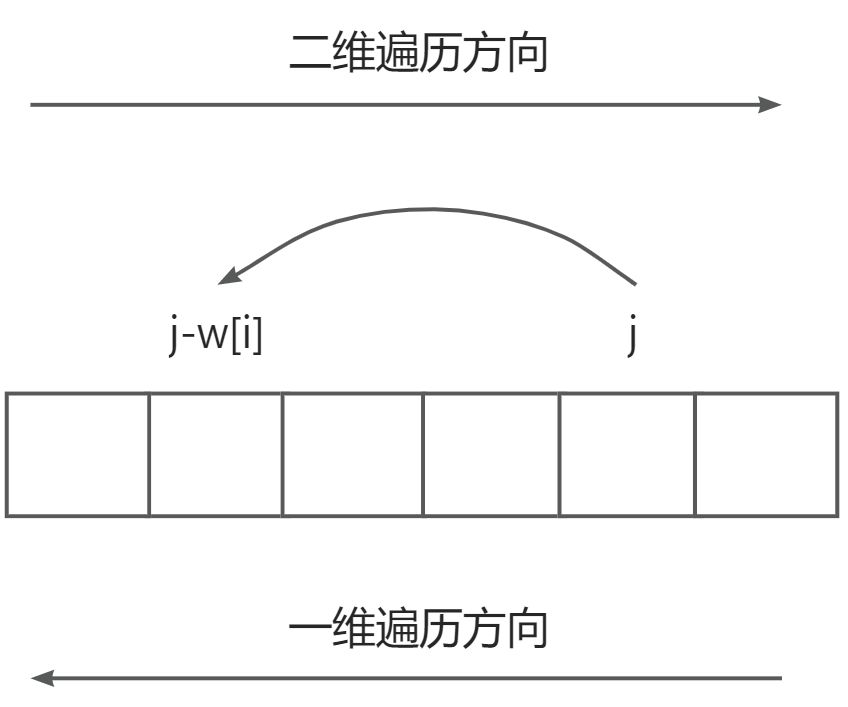
可以看出，后面的状态是用到了前面的状态的。如果还是像二维一样从左往右遍历的话，会出现这种情况：dp[j-w[i]] 被物品 i 更新了，dp[j] 也被物品 i 更新了。由于 dp[j] 是由 dp[j-w[i]] 更新过来的，相当于在重量为 j 的容器里放了两次物品 i，这和 01 背包的题目含义就冲突了：每件物品只有选和不选两种状态。
所以就要保证 dp[j] 用到的 dp[j-w[i]] 是没有被更新过的。方法也容易，反过来遍历就可以了。

初始化

一维的初始化实际上就是初始化一个物品都没用到时的价值。显然，对于任何重量的容器，不放物品，价值就是 0。初始化代码：

for(int j = 0; j <= W; j ++ ) dp[j] = 0;

容量 W 和物品 N 的遍历顺序

对于二维的形式，两种遍历方式都可以，因为不管怎么样，dp[i][j] 都是被左上角的状态更新的，所以先更新左上角的哪一个，实际上都一样。但是对于一维的形式，情况就不一样了。详细看一下两种方法的遍历的含义：

1. 先遍历容量 W，再遍历物品 N：（×）

for(int j = W; j >=0; j -- )
	for(int i = 0; i < N; i ++ ) {
    	if (j >= w[i]) dp[j] = Math.max(dp[j], dp[j - w[i]] + v[i]);
    }

这种方法，相当于是对于同一个重量 j，从 N 个物品中选 1 个，看哪个价值最大。那最后 dp[W] 表示的就是从 N 个物品中选 1 个物品时的最大价值，这显然与 01 背包的题目含义冲突了：从 N 个物品中选若干个物品时（每个物品只选一次）的最大价值。
进一步分析，为什么这种方法每次都只会用到一个物品？因为每次递推用到的 dp[j-w[i]] 都是 0，因为 j 是从大到小遍历的，递推公式相当于变成了 dp[j]=Math.max(dp[j], v[i])，那不就是 N 个物品取最大值吗？所以也进一步加深了对一维递推公式的理解：要利用一维的递推，dp[j-w[i]] 一定要叠加了前面选了物品的状态。

2. 先遍历物品 N，再遍历容量 W：（√）

for(int i = 0; i < N; i ++ )
	for(int j = W; j >=0; j -- ) {
    	if (j >= w[i]) dp[j] = Math.max(dp[j], dp[j - w[i]] + v[i]);
    }

这种方法，是先考虑前面物品的使用情况，放到 dp 中去，然后再开始考虑下一件物品。所以这种方法中，dp[j - w[i]] 是叠加了前面选了若干件物品之后的状态的。
因此，应该选择第二种遍历顺序。

时空复杂度

时间复杂度：O(NW)
空间复杂度：O(W)，空间上比二维少了一个数量级

完整代码

int N, W; // N件物品，容量为W
int w[N], v[N]; // w为大小，v为容量

/* 数组定义 */
int[] dp = new int[W + 1]; // 注意是W + 1, 因为重量会取到W
dp[j]; // 大小为j的容器时的最大价值

/* 递推公式 */
dp[j] = Math.max(dp[j], dp[j - w[i]] + v[i]);

/* 初始化 */
for(int j = 0; j <= W; j ++ ) dp[j] = 0;

/* 求解 */
// 每迭代一次i，dp就多叠加了一件物品的状态
for(int i = 0; i < N; i ++ )
	for(int j = W; j >= 0; j -- ) {
        if (j >= w[i]) dp[j] = Math.max(dp[j], dp[j - w[i]] + v[i]);
    }

/* 输出答案 */
// dp[W]: 大小为W的容器时的最大价值
return dp[W]; 

题目

问能装的最大容量，或者问能不能装满的这种题目，属性既是重量又是价值。

下面是代码随想录中，01背包问题的总结。

题目	问题转换	属性拆解
416. 分割等和子集 01 背包 求最大容量	选一堆数出来，让它们的和等于 sum / 2。 将若干个数放入大小为sum / 2的背包，问背包是否能装满？进一步，问背包能装的最大容量是否和背包容量相同？	背包容量：sum / 2。 物品体积：由于是选若干个数出来让他们的和等于 sum /2，所以物品的大小（体积）就是数的数值大小。 物品价值：这一题没有价值这个维度，只是问背包能装的最大容量。那其实就可以把数值大小看成价值。能不能装满，其实就是最后的最大价值和背包容量是否相等。 物品数量：每个数字只能选择一次。
1049. 最后一块石头的重量 II 01 背包 求最大容量	将石头分成尽可能重量相等的两堆，这样他们之间两两粉碎，就可以使得重量差值最小，所以最后剩下的石头重量也就最小。 将若干个数放入容量为 sum / 2 下取整的背包中，问总重量 - 能放的最大重量为多少？	背包容量：sum / 2。 物品体积：由于是选若干个数出来让他们的和等于 sum /2，所以物品的大小（体积）就是数的数值大小物品体积：石头重量就是体积。 这一题没有价值这个维度，只是问背包能装的最大容量。那其实就可以把石头重量看成价值。 物品数量：每个石头只能选择一次。
494. 目标和 01 背包，二维背包，求最大容量	假设加的和为x（绝对值），则减的和为sum - x，则加 - 减 = target => x - (sum - x) = target => x = (target + sum) / 2。所以，即在n个数中，选若干个数，和为(target + sum) / 2的方案数。 在n个数中，选若干个数，放入大小为(target + sum) / 2的背包，问放满有几种方案？ 前提条件： ● target + sum是偶数，否则无解 ● abs(target) <= sum，否则无解	背包容量：(target + sum) / 2。 物品体积：数值大小就是体积。 物品价值：这一题没有价值这个维度，只是问背包放满有几种方案。 物品数量：每个数字只能选择一次。
474. 一和零 01 背包 恰好装满，求方案数	这题我认为比较隐蔽，不太能看出来是背包问题。这种题目只能看一个学一个了。题目中“最多有 m 个 0 和 n 个 1”，其实蕴含了背包是个二维背包，容量是 m、n。 从 n 个字符串中选若干个字符串，放入一维体积为 m 二维体积为 n 的背包中，问最大容量是多少？	背包容量：m、n。 物品体积：每个物品有两个维度的体积，字符串中 的 0 就是第一维体积、字符串中的 1 就是第二维体积。 物品价值：同样的，这题问最大容量，所以没有价值的概念，所以把体积看成价值。 物品数量：每个数字只能选择一次。

注意416. 分割等和子集这个题和494. 目标和这个题的关系和区别。前者要判断是否能装满，因为是存在装不满的情况的。而后者是要求装满的方案数。虽然代码中没有明显判断是否能装满，但其实如果装不满的话，方案数就会为 0。