二氧化碳和全球变暖

总  结

伴随着全球气候变暖问题的日益严峻,越来越多的研究者认为二氧化碳排放是影响全球气候变化的重要因素。利用1959-2021年相关CO2浓度和相应的温度数据进行对比分析并进行预测, ,利用ARIMA模型、Winters Additive model模型、线性回归模型等对未来世界的二氧化碳浓度进行预测以及二氧化碳浓度和陆地-海洋温度之间是否存在某种关系。

经过相关研究表明: CO2浓度的确与相应温度有关，并且是显著影响，但是相应CO2浓度并不会过于增长。通过相应的时间序列预测模型进行对未来时间的CO2浓度进行预测，可以使相应研究更加精确、快速。

目  录

总  结............................................................................................................................... I

第1章 简  介................................................................................................................ 3

1.1 背景....................................................................................................................... 3

1.2 我们的工作........................................................................................................... 3

第2章 一般假设和符号说明........................................................................................ 5

2.1 一般假设............................................................................................................... 5

2.2 符号说明............................................................................................................... 5

第3章 是否同意二氧化碳级别的说法........................................................................ 6

3.1 介绍自己的观点并说明理由............................................................................... 6

3.2 根据相应模型预测二氧化碳的浓度水平........................................................... 9

3.2.1 ARIMA模型预测二氧化碳的浓度水平........................................................ 9

3.2.2 Winters Additive model模型预测二氧化碳的浓度水平.................... 11

3.2.3 线性回归模型预测二氧化碳的浓度水平................................................. 13

3.2.4 指数平滑Simple Exponential Smoothing模型预测二氧化碳的浓度水平......................................................................................................................... 17

3.3 是否同意2050年CO2浓度将达到685ppm的说法和预测............................... 20

3.3.1 是否同意相关观点..................................................................................... 20

3.3.2 预测什么时侯CO2浓度将达到685ppm.................................................... 22

第4章 探究温度和二氧化碳之间的关系.................................................................. 23

4.1 建立模型并进行论证相应问题......................................................................... 23

4.1.1 建立模型..................................................................................................... 23

4.1.1 论证相应问题............................................................................................. 24

4.2 分析1959年以来CO2浓度和陆地海洋温度之间的关系并证明.................... 25

参考文献......................................................................................................................... 29

附录................................................................................................................................. 30

第1章 简  介

1.1 背景

地球是人类的唯一的家园，是人类赖以生存的星球，正是因为地球环境适宜、拥有大量的水资源和氧气，人类才能在地球上繁衍至今，不断创造出惊人的高科技。随着人类的发展，对地球环境有很大的考验，地球环境的变化或直接影响人类在地球上的生存，如果再不重视环境问题，人类未来或会从这个地球上消失。

工业革命以后，人类活动越来越频繁，不断索取拍在地球上的资源，地球的资源已经匮乏，甚至都面临紧缺的情况。同时人类正在面临一个严峻的问题，那就是地球的表面温度不断升高，加快了两极极地地区的冰川融化和高原冻土层的融化，这些问题都给人类带来巨大的影响。

起初大家认为全球变暖，主要是因为大气层中二氧化碳的含量增高，后续根据研究发现，全球变暖和二氧化碳并没有很大关系。地球体积巨大，人类在地球上不过是像一只“小蚂蚁”，我们只关注到了地球上方大气层中的环境问题，却忽略了地球内部的变化。科学家研究发现，除了二氧化碳的含量增多以外，地球内部的压力逐渐增大，地核温度越来越高，让许多火山变得非常活跃。

1.2 我们的工作

为了更好的进行对相应结果的展示和论证的说明，我们完成了以下工作。

1.选取了从1959年到2021年之间的63个年份的CO2的含量水平以及增长水平数据的原始数据。然后通过为了更好的进行数据展示，选用2004年前后的数据并通过差值为3的等差数列进行选取相应年份数据信息进行绘制相应的折线图以便实现数据可视化。

2.通过建立了ARIMA模型、Winters Additive model模型、指数平滑模型、线性回归模型等4种模型进行分别预测大气中CO2的浓度。通过不同的实验数据集进行对不同模型进行介绍和描述，将相应数据集带入到对应的模型计算中得到对应的结果集，然后进行对结果集的分析和说明，进行论述相应的问题。并通过相应的模型进行说明具体哪一个模型的结论更加精准。

3.通过模型以及相应的算法等进行说明CO2跟温度之间的关系，进行计算回归斜率t的值，从而说明CO2跟温度之间的影响关系。

第2章 一般假设和符号说明

2.1 一般假设

为了使相应模型能够更准确的反映CO2和温度之间的关系，我们对相应建模系统中可以使用的模型方法进行类比，并作了以下假设：

1. 我们从网站收集的统计数据使真是可靠的。
2. 相应大气中的CO2浓度只和温度有关。
3. 我们选择的相应的年份中相应的CO2的浓度在不同月份中平均分布，可以通过样本来进行估计总体情况。
4. 不同年份中的CO2浓度符合相应的分布规律，可以用来衡量相应的与温度之间的关系。
5. 在一定时间内，对于一些不受相应因素影响的数据可以视为常量。

基于以上假设，我们选取了合理的数据集,并采用了相应的处理方法,建立了不同模型进行说明相应CO2和温度之间的关系。

2.2 符号说明

符号名	符号所代表的意思
d	差分阶数
H0	原假设
H1	择备假设
p	滞后阶数
q	阶数
alpha	平滑系数

第3章 是否同意二氧化碳级别的说法

    本章节主要介绍是否同意2004年3月二氧化碳的增加导致了比过去任何10年期间观察到的更大的增长这一观点。相应章节的内容主要是首先进行介绍自己的观点（同意或者不同意），并说明相应的理由。然后利用其中的多个数据模型和数据进行结合，主要用来描述过去或者预测未来大气中的二氧化碳浓度。最后对其中的每个模型进行预测全年大气中的二氧化碳浓度，并判断不同模型是否符合2050年二氧化碳浓度将达到685ppm的说法和预测，如果2050年不能达到该浓度的话，则说明一下具体某一年能到达相应的浓度。以下则是本章节的相应观点和论证。

 3.1 介绍自己的观点并说明理由

本小节主要介绍是否同意2004年3月二氧化碳的增加导致了比过去任何10年期间观察到的更大的增长的这一观点。相应的观点是不同意。相应的理由如下：

通过收集从1959年到2004年的数据进行对相应理论进行说明，但是由于相应数据共有将近45个，因此，为了更好的进行绘制相应的统计图，选取2004年以前的年份信息中进行选取每隔两年的数据，这样既不影响数据的真实性，同时还能通过相应数据进行更好的论证，使得对应数据也更加有代表性。

年份	1959	1962	1965	1968	1971	1974	1977	1980
大气中CO2的浓度	315.98	318.45	320.04	323.05	326.32	330.19	333.84	338.76
陆地-海洋温度差	0.03	0.03	-0.11	-0.08	-0.08	-0.07	0.18	0.26

年份	1983	1986	1989	1992	1995	1998	2001	2004
大气中CO2的浓度	343.15	347.61	353.20	356.54	360.97	366.84	371.32	377.70
陆地-海洋温度差	0.31	0.18	0.27	0.22	0.45	0.61	0.53	0.53

  

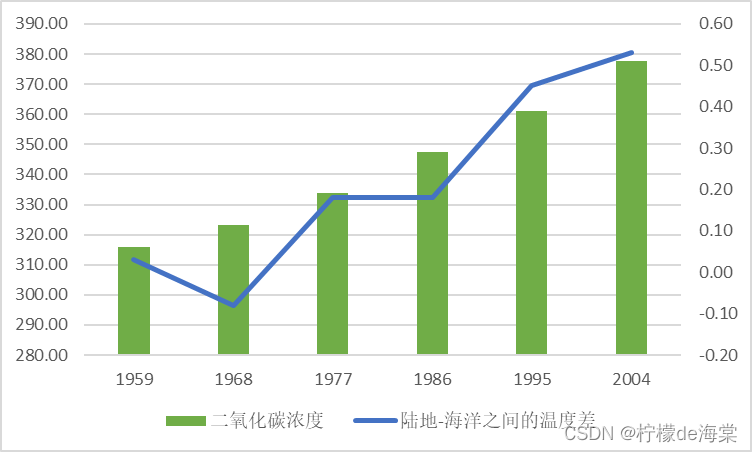
   由所给的数据集数据可知，CO2含量水平趋势从最初的1959年的315.98稳定增长到2004年的377.70，并且其中每一年都在一点点的增长，相应总体水平也呈现一个稳定增长的趋势，并且从相应数据中可以看出，2004年的CO2增长率在过去45年中处于中等水平，其在近45年的时间内，稳定增长61.72，其增长量相当于1959年的总含量水平的百分之二十。

但是如果从CO2的增长率来看的话，相应数据从最开始的0.03不规律的变化到2004年的0.53，其中1952，1962以及1983年的增长率相对来说持平，在1962年之后到1974年，相应CO2的增长率呈现负增长状态。对比每一年与上一年的CO2水平增长幅度也能得出类似的结果。因此认为2004年之后观察到更大的CO2增加有支撑证据。

然而，如果说每隔两年的数据集选取的方法使得相应数据集同样过多，相应效果不明显的话，那么同样，选用2004年前每隔10年的数据进行分析并绘制相应的折线图进行对比图如下，这样可以通过简单的数据集使得相应的结论更加有说服力，下面的折线图图像更有力说明上面的分析结论。

            

当然，上面的数据可视化分析由于根据相应的图像走向以及数值等因素进行判断，使得其结果都带有主观成分，那么我们使用t值进行检验2004年之前的CO2的增长水平与2004年之后的增长是否有显著性差异。对比两个时期的CO2的平均增长来看，在2004年之前，CO2的平均每10年增长15.02，或许增长4.46%。而在2004年之后，CO2的平均每10年增长22.86，或许增长5.94%。

Year Label	CO2 ten year change	CO2 _ ten year growth rate
after 2004	21.28	0.06
before 2004	13.80	0.040

对于10年CO2的的增长t检验，t统计量为-11.20，p值接近为0，我们应该拒绝原假设，认为2014年之后CO2的的增长更加快。

	before 2004	after 2004
mean	13.80	21.28
variance	7.13	3.43
sample size	2.67	1.85
pooled standard deviation	36.00	17.00
df	0.72
T-statisitc	51.00
T critical value ( one-tailed)	-10.40
T critical value (two-tailed)	1.68
P value ( one-tailed )	2.01
P value (two-tailed )	0.00

同样道理，对于10年CO2的增长率t值进行检验，则发现t统计量为-10.21，p值接近为0。因此，我们应该拒绝原假设，认为2004年之后10年CO2增长率更大。

3.2 根据相应模型预测二氧化碳的浓度水平

3.2.1 ARIMA模型预测二氧化碳的浓度水平

（1）模型介绍：ARIMA全称自回归积分滑动平均模型,也记作ARIMA (p,d，q),属于统计预测模型。所谓ARIMA模型,是指将非平稳时间序列转化为平稳时间序列,然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。ARMA模型根据原序列是否平稳以及回归中所含部分的不同。差分自回归滑动平均模型（ARIMA），综合了三项 AR、I（integration）、MA，是在ARMA基础上改进而来的模型。

（2）模型要求：ARMA模型的平稳性要求X的均值、方差和自协方差都是与时间无关的、有限的常数，也就说ARMA模型是针对平稳时间序列建立的模型，只能处理平稳序列。而ARIMA模型是针对非平稳时间序列建模。换句话说，非平稳时间序列要建立ARMA模型，首先需要经过差分转化为平稳时间序列，然后建立ARIMA模型。

如果非平稳时间序列Xt经过d次差分后的平稳序列Zt服从ARMA(p,q)模型，那么称原始序列Xt服从ARIMA(p,d,q)模型。也就是说，原始序列是I(d)序列，d次差分后是平稳序列I(0)。平稳序列I(0)服从ARMA模型，而非平稳序列I(d)服从ARIMA模型。

  基于ARMA添加差分处理，在前述模型上多了一个差分阶数需要进行确定，表达式如下：

1-i=1p∅i Li1-Ld xt=(1+ i=1qθiLi)ϵt

ARIMA模型虽然不要求时间序列数据平稳，但是需要确定差分阶数d。对CO2增长（CO2水平的一阶差分）进行进行ADF（单位根）检验，判断是否平稳序列。

（3）ARIMA建模基本步骤:

1.获取被观测系统时间序列数据;若不是时间序列数据需要转换为时间序列数据。

2.对数据绘图,观测是否为平稳时间序列;对于非平稳时间序列要先进行d阶差分运算,化为平稳时间序列。

3.要对平稳时间序列分别求得其自相关系数ACF和偏自相关系数PACF,通过对自相关图和偏自相关图的分析,得到最佳的阶层p和阶数q。

4.由以上得到的d得到ARIMA模型。然后开始对得到的模型进行模型检验。

（4）ARIMA模型计算过程:

根据第三步建模步骤得到以下解题思路和过程。

对CO2浓度进行差分运算进行ADF检验,可以得出The ADF Statistic的数值为-0.759689。The p value的数值为0.830677。

然后进行取0.05的显著性水平，得到的P值为0.83，大于0.05，因此不拒绝原假设，CO2增长（CO2水平的一阶差分）非平稳。

继续对CO2增长差分（CO2的二阶差分）进行ADF检验。可以得出The ADF Statistic的数值为-5.733053。The p value的数值为0.000001。

P值接近0，有足够的证据拒绝原假设，意味着CO2经过2次差分后，得到平稳序列，也意味着ARIMA(p,d,q)中的参数d为2. 随后确定模型参数p和q的阶数。

最后使用网格搜索算法进行遍历搜索，以AIC为模型的评价指标，搜索AIC最小的ARIMA模型，最后确定最佳模型为ARIMA(2,2,3)。

相应模型参数和模型评价以及模型计算结果如下：

	coef	Stderr	z	p>|z|	[0.025	0.975]
ar.L1	-0.35	0.060	-5.79	0.00	-0.46	-0.23
ar.L2	-1.00	0.034	-27.29	0.00	-1.07	-0.93
ma.L1	-0.39	0.89	-0.43	0.66	-2.14	1.35
ma.L2	0.76	5.14	0.15	0.88	-9.31	10.82
ma.L3	0.72	4.26	-0.17	0.87	-9.07	7.62
sigma2	0.18	1.01	0.17	0.86	-1.80	2.15

模型评价参数	评价结果
RMSE	0.43456
MSE	0.18889
MAE	0.32963
MAPE	0.09252
Theil’s U	1.49116e-06

3.2.2 Winters Additive model模型预测二氧化碳的浓度水平

（1）模型介绍：如果数据是平稳或水平型的,则滑动平均或一次指数平滑法是合适的:若数据中表现出线性趋势,则二次滑动平均或二次指数平滑的线性模型即可处理:但是,若数据中隐藏着季节成分,则上述方法就无能为力。Winters Additive model模型预测方法主要由以下几部分构成：

Lt= αYt- St-s+(1-α)(Lt-1+ Tt-1)

Tt=βLt-Lt-1+(1-β)Tt-1

                                    

St=γYt-Lt+(1-γ)St-s

Yt+p=Lt+ Ttp+ St+p-s

其中L是水平项level，T是趋势项Trend,  S是季节性项Seasonality. Y_t 表示时间t下的CO2值。

（2）模型要求：Winters Additive model模型相对ARIMA模型来说简单有效的多，假设但是要求相应数据数据服从两点，一个是相应数据时呈递增或者递减趋势的，另一个是相应数据需要服从一个周期变化。

（3）Winters Additive model模型计算过程:

从模型方程式来看，模型有三个参数alpha、beta、gamma。我们同样使用网格搜索算法遍历每一组参数，选择AIC最小的模型作为最佳模型。

相应计算出来的模型参数以及模型评价如下所示：

最佳模型参数	最佳模型参数数值
Best alpha	0.71
Best beta	0.30
Best gamma	0.93

模型评价参数	评价结果
RMSE	0.49010
MSE	0.24020
MAE	0.36941
MAPE	0.10334
Theil’s U	1.90279e-06

3.2.3 线性回归模型预测二氧化碳的浓度水平

   （1）模型介绍：任何事物都不可能孤立地存在,其变化和发展往往会受到许多因素地制约或影响。例如,商品地需求量取决于消费者地可支配收入、商品地价格和其代用品地价格。生产费用由所生产的产品数量及各种投入要素的单位成本构成:产品的产量取决于投入的资金、劳力、各种原材料乃至市场的需求等等。如果能对其所谓回归分析,就是在统计“平均”的意义下,定量地描述所考察地变量之间的数量关系;它一般用来刻化一个预测对象(因变量)Y与一个或多个预测因子(自变量)X之间地相关关系,其表现形式是由Y、X和f(Y,X,0,ε)=0,或Y=f(x, θ)+c以上两式中的ε表示随机误差。习惯上,取f为X和θ的显函数。如果X仅表示一个解释变量,则称相应的模型为一元回归模型,否则称为多元回归模型;如果f关于x和θ都是线性的,称其为线性回归模型。

（2）模型要求：

1.要预测的变量 y 与自变量 x 的关系是线性的。

2.各项误差服从正太分布，均值为0，与 x 同方差。

3.变量 x 的分布要有变异性。

4.多元线性回归中不同特征之间应该相互独立，避免线性相关。

（3）线性回归模型计算过程:

根据科学家们的共识，CO2主要由人类活动所产生，这也意味着人口的多少会直接影响到CO2的增长水平。因此，我们在世界银行中找到自1958年以来每一年的地球总人口数量、人口净增长数据，相应数据如下所示：

另外，我们的任务是预测，因此不能使用相同时期的人口数据来预测CO2水平，而是应该使用过去的人口数据来预测未来的CO2趋势。我们在数据表中新构建一个变量—去年的总人口，结合题目提供的CO2数据以及陆地-海洋温度差数据，计算相关矩阵，其热力图如下：可以看出CO2水平与温度差、同年的总人口、去年的总人口都高度线性相关。

          为了避免多种共线性问题，我们只使用去年的总人口（单位：百万人）来作为回归自变量，构建简单线性回归模型，预测下一年的CO2水平。

                           

相应计算出来的模型可视化以及模型评价如下所示：

模型评价参数	评价结果
RMSE	3.25738
MSE	10.61052
MAE	2.66984
MAPE	0.74138
Theil’s U	8.43345e-05

3.2.4 指数平滑Simple Exponential Smoothing模型预测二氧化碳的浓度水平

   （1）模型介绍：指数平滑可继续拆分为一次平滑，二次平滑和三次平滑（即Holt-Winters法），一次平滑法为历史数据的加权预测，二次平滑法适用于具有一定线性趋势的数据，三次平滑法在二次平滑法基础上再平滑一次，其适用于具有一定曲线趋势关系时使用，通常情况下使用三次平滑法较多。指数平滑方法为过去的观测分配指数递减的权重。得到的观测值越近，权重就越大。

（2）模型要求：

    无论是那种平滑法，其均涉及初始值S0和平滑系数alpha共两个参数值。

初始值是平滑的最初起点值，一般取数据前1期，2期，3期，4期或5期的平均值作为初始值，如果数据序列越少则初始值S0应该取更多前几期的平均值，因为数据序列较少时前期的重要性相对较高。

alpha值参数，其意识在于新数据的权重，alpha值的取值范围为0~1,越大意味着新数据所占的权重越高而原预测值所占权重越低。如果说数据波动不大，一般alpha值取的较小些比如0.1~0.5之间，如果数据波动较大且alpha值取值相对较大些，比如0.6~0.8之间。

（3）Simple Exponential Smoothing模型计算过程:

Simple Exponential Smoothing模型计算公式为：

Lt= αYt-1+(1-α)Lt-1

模型评价参数	评价结果
RMSE	1.75439
MSE	3.07789
MAE	1.62208
MAPE	0.44462
Theil’s U	2.43823e-05

   由于此模型不具有长期预测能力，因此，本次研究不对其进行过多使用。

3.3 是否同意2050年CO2浓度将达到685ppm的说法和预测

3.3.1 是否同意相关观点

对于2050年CO2浓度将达到685ppm的说法和预测，本人不同意相应观点。相关理由如下：

由于上一章节介绍的ARIMA模型和Winters Additive Model模型都属于时间序列模型，因此只需要根据其相应模型本身的历史数据就能进行实现预测未来这一功能。

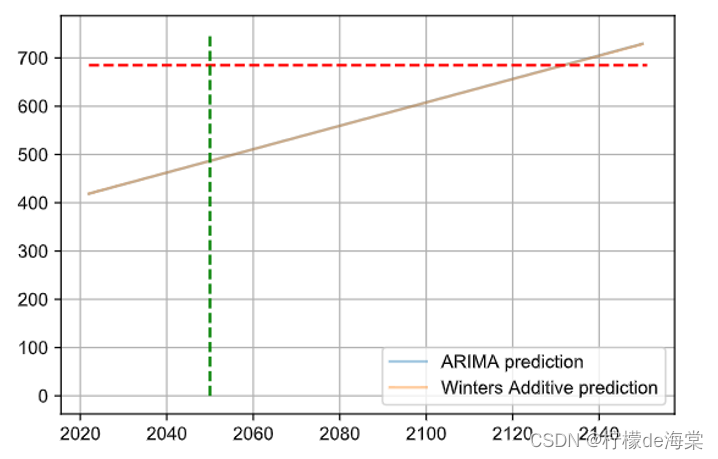
根据ARIMA模型进行预测的结果是在2050年，大气中的的CO2浓度预测值为486.72ppm。而根据Winters Additive模型进行预测的结果是在2050年，大气中的的CO2浓度预测值为486.67ppm。根据两个模型之间的对比预测，发现两个模型的预测结果非常相近。

由于两个模型计算的2050年大气中的的CO2浓度预测值都没有达到预测的685ppm，因此，将相依时间进行往后延50年，也就是2100年，根据模型进行判断2100年相应数据能否达到预测值。

根据ARIMA模型进行预测的在2100年，大气中的的CO2浓度预测值为608.14ppm。而根据Winters Additive模型进行预测的在2100年，大气中的的CO2浓度预测值为607.74ppm。虽然相应两个模型的预测值仍然都没有达到相应的观点，因此并不同意相应的说法。

Year	ARIMA	Winters Additive
2050	486.72	486.67
2100	608.14	607.74

3.3.2 预测什么时侯CO2浓度将达到685ppm

由上一小节的两个时间序列模型的预测可以得知，至少需要到2132年，CO2水平才会到达685 PPM。

然而对于线性回归模型来说，CO2浓度跟相应世界总人口数有关，同时并不需要额外构建别的模型进行预测2049年和2099年的世界总人口。根据相应可找到的世界银行进行预测出的未来每一年的人口总数作为相应的数据源对象，我们只需要直接参考世界银行的人口预测，并用于我们的回归模型预测即可。

根据世界银行的预测，在2049年，世界总人口为96.6亿，而回归模型的CO2预测值为446.85。在2099年，世界总人口为103.6亿，而回归模型的CO2预测值为459.71。

根据世界银行的预测，世界人口在2090年左右达到巅峰，巅峰人口为104.3亿。

但根据模型回归模型的预测，在世界人口巅峰时期，CO2的预测值仍然不超过500，这将意味着CO2永远都不会超过685 PPM。

第4章 探究温度和二氧化碳之间的关系

本章节主要任务是研究温度和二氧化碳之间的关系，并通过前一章节和相应温度数据集中的相应数据和理论知识，进行研究和比较陆地-海洋温度和二氧化碳浓度之间的关系。相应的研究步骤是首先通过建立一个模型进行预测未来陆地-海洋温度的变化，然后在进行分析1959年之后的二氧化碳浓度和陆地海洋温度之间的关系，并进行证明相应的关系或者相应之间无关系。最后说明相应模型的可靠性以及相应模型预测的能力进行简单说明。

4.1 建立模型并进行论证相应问题

4.1.1 建立模型

    由于相应温度变化比较平稳，因此，此处依然可以用ARIMA模型来进行预测陆地-海洋温度变化时间序列。

   与前文中预测CO2浓度水平相类似，同样使用网格搜索算法搜索最佳模型阶数p,d,q，并选择最小AIC的模型作为最佳模型。

最佳模型为ARIMA(0,1,2)。模型系数估计如下：

	coef	Stderr	z	p>|z|	[0.025	0.975]
intercept	0.02	0.00	4.73	0.00	-0.01	0.02
ma.L1	-0.57	0.134	-4.17	0.00	-0.83	-0.30
ma.L2	-0.20	0.14	-1.45	0.15	-0.47	0.07
sigma2	0.01	0.00	4.92	0.00	-0.01	0.01

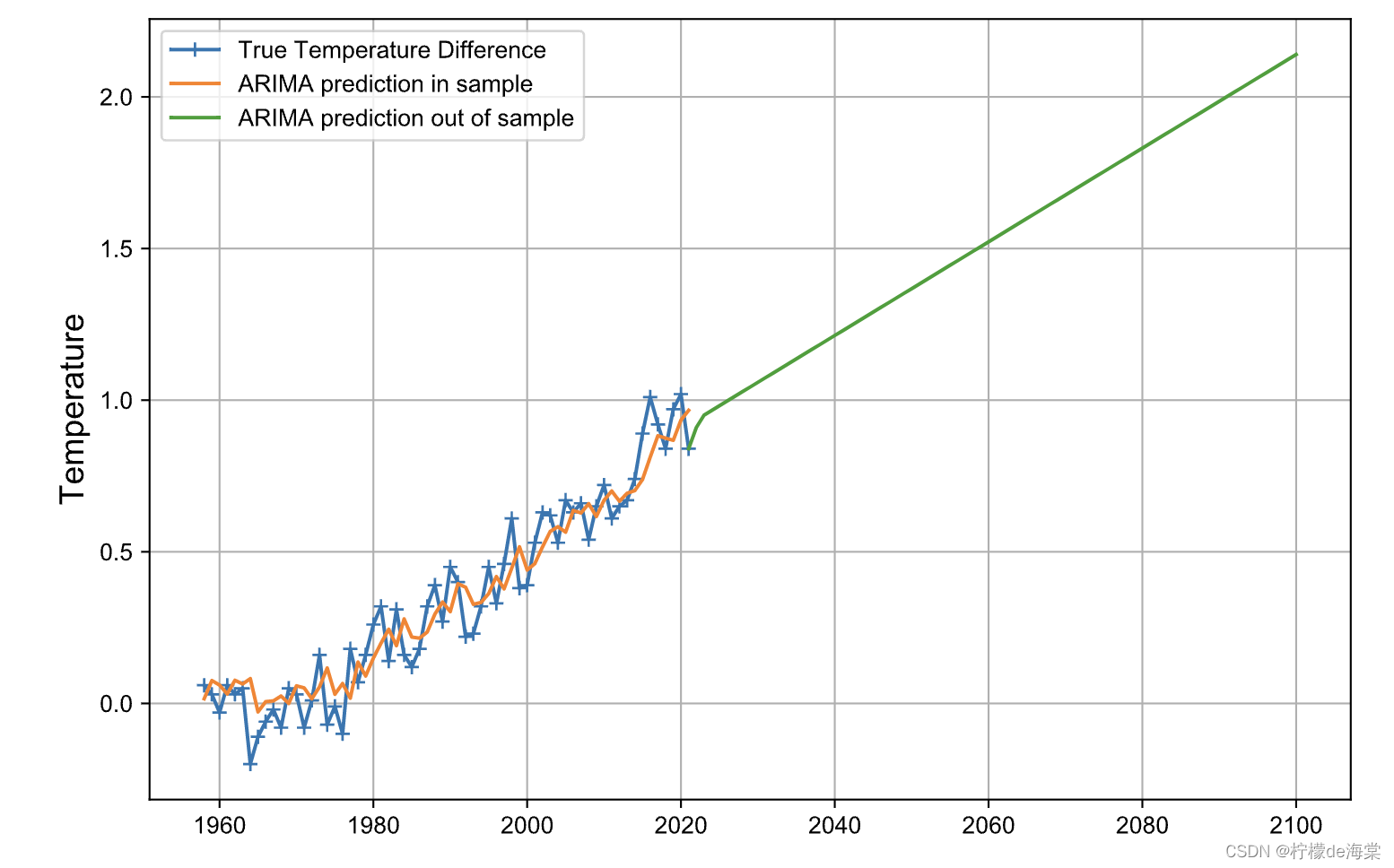
相应计算出来的模型预测效果图以及模型评价如下所示：

模型评价参数	评价结果
RMSE	0.09973
MSE	0.00995
MAE	0.08388
MAPE	60.07637
Theil’s U	0.04672

4.1.1 论证相应问题

   

    由于ARIMA模型具有独特的预测功能，因此进行设计了相应的数据带入计算以及相应数据可视化分析可以得知：

  （1）陆地-海洋的平均温度变化1.25℃的时间在2043年，相应温度变化的具体数值是1.259539.

  （2）陆地-海洋的平均温度变化1.5℃的时间在2059年，相应温度变化的具体数值是1.506616.

  （3）陆地-海洋的平均温度变化2℃的时间在2091年，相应温度变化的具体数值是2.000769.

4.2 分析1959年以来CO2浓度和陆地海洋温度之间的关系并证明    

根据相应模型的预测值进行设计相应的散点图如下：

根据散点图可知，CO2和温度差具有很明显的线性正相关，而且相关系数高达0.9613.

以CO2为自变量，温度差为因变量，构建简单线性回归模型：回归估计如下：

Model	OLS	Adj. R-squared:	0.923
Dependent Variable:	Temperature	AIC	-122.18
Date	2022-11-06 00:26	BIC:	-117.89
No. Observations:	63	Log-Likelihood:	63.09
Df Model:	1	F-statistic:	743.00
Df Residuals:	61	Prob (F-statistic):	7.34e-36
R-squared:	0.92	Scale:	0.01

	coef	Stderr	t	p>|t|	[0.025	0.975]
const	-3.39	0.14	-24.61	0.00	-3.66	-3.11
CO2	0.011	0.00	27.26	0.00	0.01	0.01

回归斜率为0.0105，意味着当CO2每提高1PPM时，温度差平均提高0.0105摄氏度。回归斜率的t检验统计量为27.26，p值接近0，意味着回归斜率是显著的。换句话说，CO2对温度差的影响是显著的。

4.3介绍模型的可靠性以及相应模型预测的能力

   由于此模型的主要功能是进行预测温度差，那么就需要进行对CO2浓度进行预测，但是对于前文中预测CO2浓度的模型已经进行介绍过。并且根据前文对CO2浓度的预测模型的相应具体表现来看，其模型在短期预测上会相应精准一些，相应的临界值在10年左右，而对相应长期预测来说。其存在较大的误差。

参考文献

[1]裴克毅, 孙绍增, 黄丽坤. 全球变暖与二氧化碳减排[J]. 节能技术, 2005, 23(3):5.

[2]张秋明. 自然界硅酸盐风化作用与温度的关系:对大气圈CO2长期聚集及全球变暖…[J]. 国外地质科技, 1994, 000(007):46-48.

[3]张含. 大气二氧化碳,全球变暖,海洋酸化与海洋碳循环相互作用的模拟研究[D]. 浙江大学, 2018.

[4]张静亚、李停停、游晓慧. 安徽省二氧化碳排放量预测分析——基于ARIMA模型[J]. 科技经济导刊, 2020, v.28;No.723(25):7-9.    

[5]林佳敏, 陈金良, 林晶晶,等. BP神经网络和ARIMA模型对污水处理厂出水总氮浓度的模拟预测[J]. 环境工程技术学报, 2019, 9(5):6.

[6]郑卓, 曹辉, 高鹤元,等. 基于加权马尔可夫链修正的ARIMA预测模型的研究[J]. 计算机应用与软件, 2020(012):037.

[7]陈美, 王红芹, 程铁信. 综合Winters模型和ARMA模型预测GDP[J]. 天津工业大学学报, 2007, 26(5):4.

[8]杨博文, 迟卫军, 付凌雨,等. ARIMA模型与Holt-Winters模型在乳腺外科出院人数预测中的应用[J]. 中国病案, 2017, 18(1):5.

[9]王培刚, 周长城. 当前中国居民收入差距扩大的实证分析与动态研究——基于多元线性回归模型的阐释[J]. 管理世界, 2005(11):11.  

[10]彭鹏, 彭佳红. 基于多元线性回归模型的电力负荷预测研究[J]. 中国安全生产科学技术, 2011, 07(009):158-161.

[11]欧阳资生, 赵霞. 基于指数回归模型的极值指数估计的门限选择[J]. 数理统计与管理, 2006, 25(6).

[12]刘琼芳, 张宗益, 吴俊. 基于指数回归模型的中小企业板极端风险度量[J]. 管理工程学报, 2011, 25(2):5.

附录

ADF单位根检验：

一阶AR模型即AR(1)的情况的模型如下：

rt= α1rt-1+ wt

如果α1=1，该模型就是随机游走，我们知道它是不平稳的。换个思路想象一下，当α 1 = 1 \alpha_1=1α

1

​

 =1，那么前一时刻的收益率对当下时刻的影响是100%的，不会减弱；那么就算是很远的某个时刻，当下对它的影响还是不会消除，所以方差（表现在波动）是受前面所有时刻的影响，是和t tt相关的，因此不平稳；

如果α 1 > 1 \alpha_1\gt1α

1

​

 >1，那么当前时刻的波动不仅受前面时刻的影响，还被放大了，所以肯定不平稳；

只有当α 1 < 1 \alpha_1\lt1α

1

​

 <1的时候，前面时刻的波动对当前时刻的影响会逐渐减小。可以计算此时的自协方差以及自相关系数是一个固定值。所以这种情况下，序列是平稳的。