Kd树(C++实现建树，插入结点，删除结点，找最邻近点)

最新推荐文章于 2025-03-27 15:25:03 发布

Oo喵生oO

最新推荐文章于 2025-03-27 15:25:03 发布

阅读量5.8k

点赞数 10

分类专栏：几何体数据结构文章标签：数据结构

本文链接：https://blog.csdn.net/dive_shallow/article/details/113136145

版权

本文详细介绍了Kd树的概念及其在二维空间中的基本操作，包括建树、插入结点、删除结点和寻找最邻近点的思路与具体实现。通过实例展示了如何使用Kd树进行点的组织，以提高查找效率。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Kd树的定义：

Kd树是一棵二叉树，对它的每一个结点（叶结点除外）都设定一个划分，使得它左子树上的点的某一维度（与划分相同的维度）都满足比它的划分小，右子树上的点某一维度（与划分相同的维度）都满足比它的划分大。

Kd树的基本操作（都以二维的为例）：

建立Kd树：

思路：

肯定是想建立一棵叶子结点相对均匀（不同的范围差别大，容易找）的二叉树，这样在后面找最邻近点的时候查找的效率会高很多。对于给定的n个点，求出x方向和y方向的方差，比较x方向和y方向方差的大小，如果x方向的方差比y方向的方差大，则本结点在x方向上划分，否则本结点在y方向上划分，这样子建出来的树，点是相对分散的，树就是相对来说较为平衡的。

代码实现：

具体的思路是，先根据方差大小确定划分是在x方向还是y方向，如果是在x方向，就按照点的x坐标对给定的点数组从小到大排序，找到x是中位数的那个点v，然后对于x坐标小于v的所有点，建立在左子树上，对于所有x坐标大于v的所有点，建立在右子树上，如果划分在y方向，就按照点的y坐标对给定的点数组从小到大排序，找到y是中位数的那个点w，然后对于y坐标小于w的所有点建立在左子树上，对于所有y坐标大于w的所有点建立在右子树上。按照这个原则递归建立左子树和右子树直到点数组的左右端点相等即以本结点为根节点的树只有一个结点为止。

void KdTree::BuildTree(Point* pointArray,int l,int r)
{
	//这里的方差相当于乘了n，因为只比较大小 
	//x方向和y方向上的方差 ，和 
	float sdx,sdy,sumx,sumy;
	for(int i = l; i < r; ++i)
	{
	    sumx += pointArray[i].x;
		sumy += pointArray[i].y;	
	}
	//得到平均数 
	float avex = sumx/(r - l),avey = sumy/(r - l);
	//计算方差
	for(int i = l; i < r; ++i)
	{
	    sdx += pow(pointArray[i].x - avex,2);
	    sdy += pow(pointArray[i].y - avey,2);
	}
	int m = (l + r)/2;
	if(sdx > sdy)
	{
		sort(pointArray + l,pointArray + r,XSortFunc);//x排序并找到中间的那个点
		splitX = pointArray[m].x;//本结点是在x方向进行了划分 
		splitY = 0;//y方向没有划分
	}
	else
	{
	    sort(pointArray + l,pointArray + r,YSortFunc);//y排序并找到中间的那个点 
	    splitY = pointArray[m].y;
	    splitX = 0;
	}
	//当前结点设置为中位数 
	point = pointArray[m];
	//[l,r]的区间是左闭右开的 
	if(m > l)
	{ 
	    
	    leftTree = new KdTree();
	    leftTree->BuildTree(pointArray,l,m);//递归构建左子树
    }
    if(m < r - 1)
    {
	    rightTree = new KdTree();
	    rightTree->BuildTree(pointArray,m+1 ,r);//递归构建右子树
	}

	
}

具体操作一下：

比如要以(2,3),(3,4),(4,6),(8,6),(12,8),(13,10),这六个点为点数组，建立一棵Kd树。

第一轮判断x方向的方差明显比y方向上的方差要大，那肯定是在x方向上划分，且x为中位数的点是(8,6)，所以第一轮先建一个(8,6)，同时条件树也要画一下，便于理解：

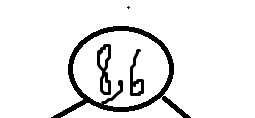
第二轮要用(2,3),(3,4),(4,6)递归建立的是它的左子树，发现左子树上y方向的方差比x方向上更大，于是找到y坐标为中位数的点，建在左子树上，并以4为划分，继续建立它的左子树。

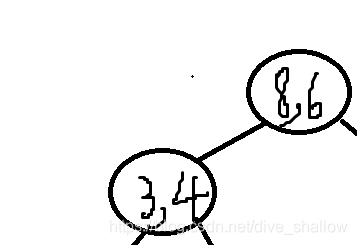
第三轮要用(2,3)建立(3,4)的左子树，只有一个点了，所以建好后就发现数组中l和r之间只有一个元素了，就回退到上一层。

第四轮回退到了(3,4)，用(4,6)建立(3,4)的右子树，然后同理回退到上一层。

从第五轮开始要建根结点的右子树了，这里不再详细赘述，最终建好的树如图:

插入结点

思路：

就跟二叉搜索树差不多，对于要被插入的结点，先根据x和y方向上的划分确定它在左子树还是在右子树，然后递归插入就可以。

具体实现：

对于要被插入的结点v，先找到当前根节点的划分是x还是y，如果是以x为划分，v的x坐标小于当前根节点的x坐标，那么v应该位于当前根结点的左子树，否则，v应该位于当前根结点的右子树，如果是以y为划分，v的坐标小于当前根节点的y坐标，那么v应该位于当前根结点的左子树，否则，v应该位于当前根结点的右子树，

如果v位于当前根结点的左子树，并且当前根节点的左子树为空，那么当前根结点的左孩子直接设置为v并且回退，如果v位于当前根结点的右子树，并且当前根结点的右子树为空，那么当前根结点右孩子直接设置为v并且回退。

void KdTree::Insert(Point point)
{
	
	//只有一个孩子 
	if(!leftTree && rightTree)
	{
		if(isLeftTreeNode(point))
		{
			//cout<<this->point<<endl;
			leftTree = new KdTree(point,NULL,NULL,0,point.y);
			return;
		}
	}
	
	if(!rightTree && leftTree)
	{
		if(isRightTreeNode(point))
		{
			//cout<<this->point<<endl;
			rightTree = new KdTree(point,NULL,NULL,0,point.y);
			return;
		}
	}
	
	//叶结点 
	if(!leftTree && !rightTree)
	{
		//两个点比较xy方差大小，看差值就可以 
		if(abs(point.x - this->point.x) > abs(point.y - this->point.y))
		{

最低0.47元/天解锁文章