1.示例引入
比如说你在京东选购手机iphone和note7:
消费者用过后,会有相关的评分。
假设评分如下:
评分 iphone note7
小a 4 5
小b 4 3
小c 2 3
小d 3 ?
问题:请猜测一下小d可能会给“note7”打多少分?
思路:把两个手机的平均差值求出来,iphone减去note7的平均偏差:[(4-5)+(4-3)+(2-3)]/3=-0.333。一个新客户比如小d,只吃了iphone评分为3分,那么可以猜测她对note7的评分为:3-(-0.333)=3.333
这就是slope one 算法的基本思路,非常非常的简单。
2.slope one 算法思想
Slope One 算法是由 Daniel Lemire 教授在 2005 年提出的一个Item-Based 的协同过滤推荐算法。和其它类似算法相比, 它的最大优点在于算法很简单, 易于实现, 执行效率高, 同时推荐的准确性相对较高。
Slope One算法是基于不同物品之间的评分差的线性算法,预测用户对物品评分的个性化算法。主要两步:
Step1:计算物品之间的评分差的均值,记为物品间的评分偏差(两物品同时被评分);
Step2:根据物品间的评分偏差和用户的历史评分,预测用户对未评分的物品的评分。
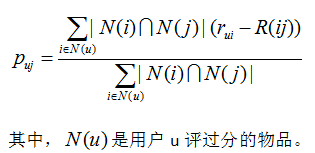
Step3:将预测评分排序,取topN对应的物品推荐给用户。
举例:
假设有100个人对物品A和物品B打分了,R(AB)表示这100个人对A和B打分的平均偏差;有1000个人对物品B和物品C打分了, R(CB)表示这1000个人对C和B打分的平均偏差;
3.Python实现
3.1数据
def loadData():
items={'A':{1:5,2:3},
'B':{1:3,2:4,3:2},
'C':{1:2,3:5}}
users={1:{'A':5,'B':3,'C':2},
2:{'A':3,'B':4},
3:{'B':2,'C':5}}
return items,users3.2物品间评分偏差
#***计算物品之间的评分差
#items:从物品角度,考虑评分
#users:从用户角度,考虑评分
def buildAverageDiffs(items,users,averages):
#遍历每条物品-用户评分数据
for itemId in items:
for otherItemId in items:
average=0.0 #物品间的评分偏差均值
userRatingPairCount=0 #两件物品均评过分的用户数
if itemId!=otherItemId: #若无不同的物品项
for userId in users: #遍历用户-物品评分数
userRatings=users[userId] #每条数据为用户对物品的评分
#当前物品项在用户的评分数据中,且用户也对其他物品由评分
if itemId in userRatings and otherItemId in userRatings:
#两件物品均评过分的用户数加1
userRatingPairCount+=1
#评分偏差为每项当前物品评分-其他物品评分求和
average+=(userRatings[otherItemId]-userRatings[itemId])
averages[(itemId,otherItemId)]=average/userRatingPairCount3.3预估评分
#***预测评分
#users:用户对物品的评分数据
#items:物品由哪些用户评分的数据
#averages:计算的评分偏差
#targetUserId:被推荐的用户
#targetItemId:被推荐的物品
def suggestedRating(users,items,averages,targetUserId,targetItemId):
runningRatingCount=0 #预测评分的分母
weightedRatingTotal=0.0 #分子
for i in users[targetUserId]:
#物品i和物品targetItemId共同评分的用户数
ratingCount=userWhoRatedBoth(users,i,targetItemId)
#分子
weightedRatingTotal+=(users[targetUserId][i]-averages[(targetItemId,i)])\
*ratingCount
#分母
runningRatingCount+=ratingCount
#返回预测评分
return weightedRatingTotal/runningRatingCount统计两物品共同评分的用户数
# 物品itemId1与itemId2共同有多少用户评分
def userWhoRatedBoth(users,itemId1,itemId2):
count=0
#用户-物品评分数据
for userId in users:
#用户对物品itemId1与itemId2都评过分则计数加1
if itemId1 in users[userId] and itemId2 in users[userId]:
count+=1
return count
3.4测试结果:
if __name__=='__main__':
items,users=loadData()
averages={}
#计算物品之间的评分差
buildAverageDiffs(items,users,averages)
#预测评分:用户2对物品C的评分
predictRating=suggestedRating(users,items,averages,2,'C')
print 'Guess the user will rate the score :',predictRating
结果:用户2对物品C的预测分值为
Guess the user will rate the score : 3.33333333333
4.slopeOne使用场景
该算法适用于物品更新不频繁,数量相对较稳定并且物品数目明显小于用户数的场景。依赖用户的用户行为日志和物品偏好的相关内容。
优点:
1.算法简单,易于实现,执行效率高;
2.可以发现用户潜在的兴趣爱好;
缺点:
依赖用户行为,存在冷启动问题和稀疏性问题。
























 780
780

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








