【数据结构】堆排序、插入、删除

本文图片均来自于网络

堆定义：n个关键字序列称为堆，当且仅当该序列满足下列两个条件中的一个：
$L(i)⩽L(2i)且L(i)⩽L(2i+1)$ ① 小根堆
$L(i)⩾L(2i)且L(i)⩾L(2i+1)$ ② 大根堆
其中$1⩽i⩽\lfloor n/2\rfloor$。
大根堆：任意一个节点的值均大于等于它的左右孩子的值，位于堆顶的节点值最大。
小根堆：任意一个节点的值均小于等于它的左右孩子的值，位于堆顶的节点值最小。

堆排序：

堆排序(Heapsort)是指利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。可以利用数组的特点快速定位指定索引的元素。堆分为大根堆和小根堆，是完全二叉树。

完全二叉树：除了最后一层之外的其他每一层都被完全填充，每一层从左到右的填充数据，不能空缺。

铺垫：

实际上要排序的是一个数组 int[] arr={3, 4, 5, 6, 7, 0, 2, 9, 8}，上面的堆是我们幻想出来的，然后知道了arr数组的下标 $i$ 后，我们可以得出它的父节点是$（i-1）/2$，它的左孩子是$2\ast i+1$，它的右孩子是$2\ast i+2$。

堆排序的实现步骤

• 把一个数组调整为大根堆（heapInsert）
  假设当前节点的下标为i，那么它的父亲节点为(i-1)/2，每次heapInsert的时候就把insert进来的节点与它的父亲节点进行比较，比它的父节点大就交换，一直重复调整。
• 每次把堆顶放到最后的节点位置，然后调整整个堆为大根堆（heapify）
  每次把堆顶的节点放到最后，然后堆大小减1，然后调整为大根堆，一直重复，直到大根堆的大小为0为止。

一句话概括就是：建立初始堆，由于堆本身特点（堆顶元素就是最大值或者最小值）输出堆顶元素后，将堆底元素送入堆顶，向下调整继续保持大根堆或小根堆的性质，如此重复，直到堆中仅仅剩下一个元素为止。

堆的存储：

一般都用数组来表示堆，$i$结点的父结点下标就为$(i–1)/2$。它的左右子结点下标分别为$2\ast i+1$和$2\ast i+2$。如第0个结点左右子结点下标分别为1和2。

堆的操作：buildHeap 堆化数组

对于叶子节点，不用调整次序，根据满二叉树的性质，叶子节点比内部节点的个数多1.所以i=n/2 -1 ，不用从n开始。

堆的操作：insert

插入一个元素：新元素被加入到heap的末尾，然后更新树以恢复堆的次序。
每次插入都是将新数据放在数组最后。可以发现从这个新数据的父结点到根结点必然为一个有序的数列，现在的任务是将这个新数据插入到这个有序数据中——这就类似于直接插入排序中将一个数据并入到有序区间中。
小根堆插入动图：

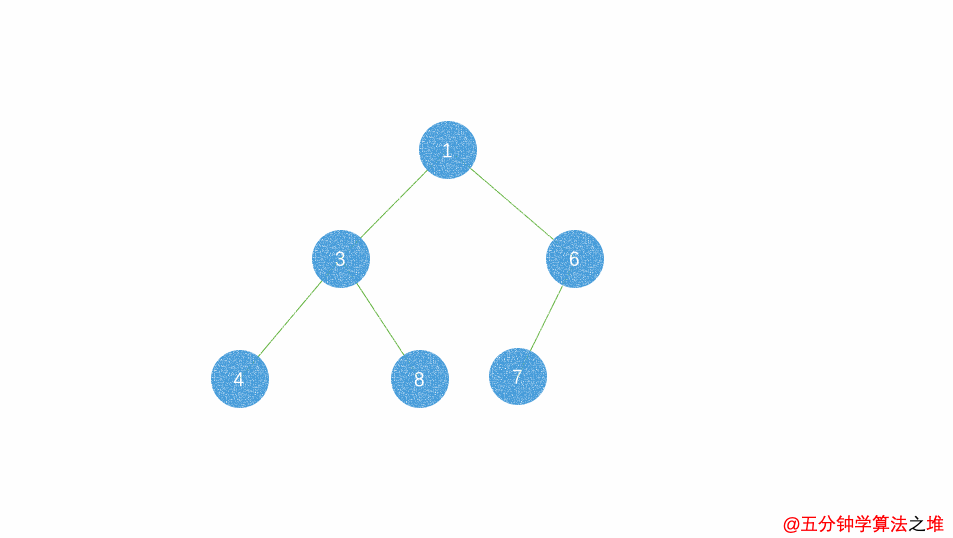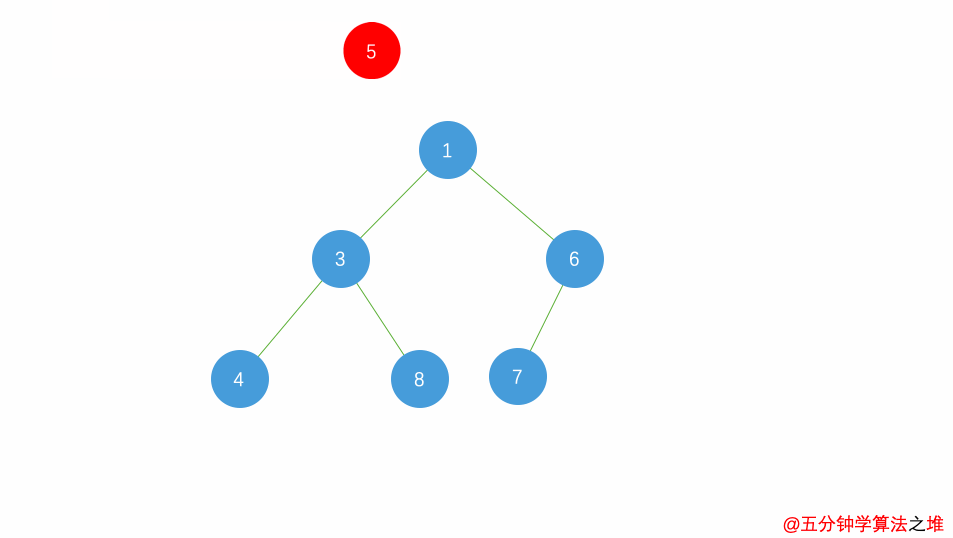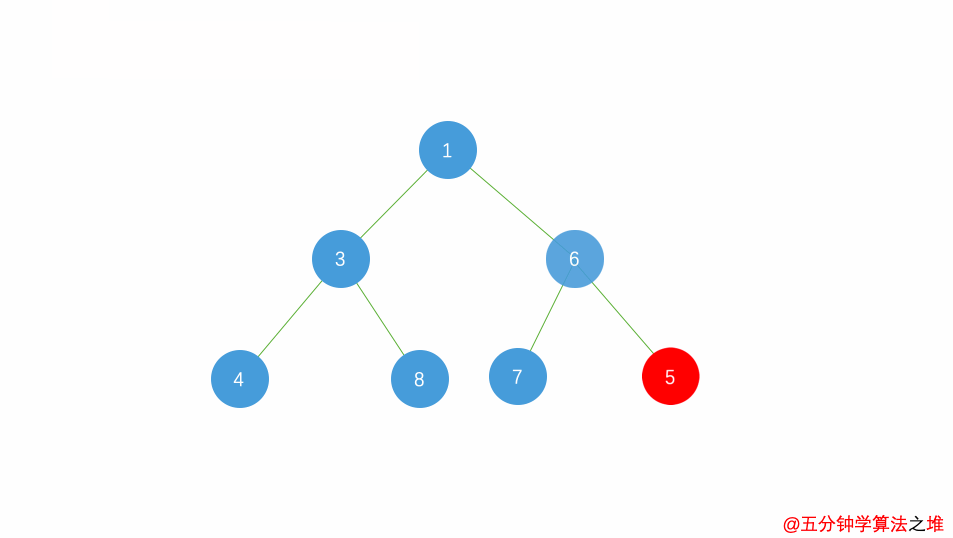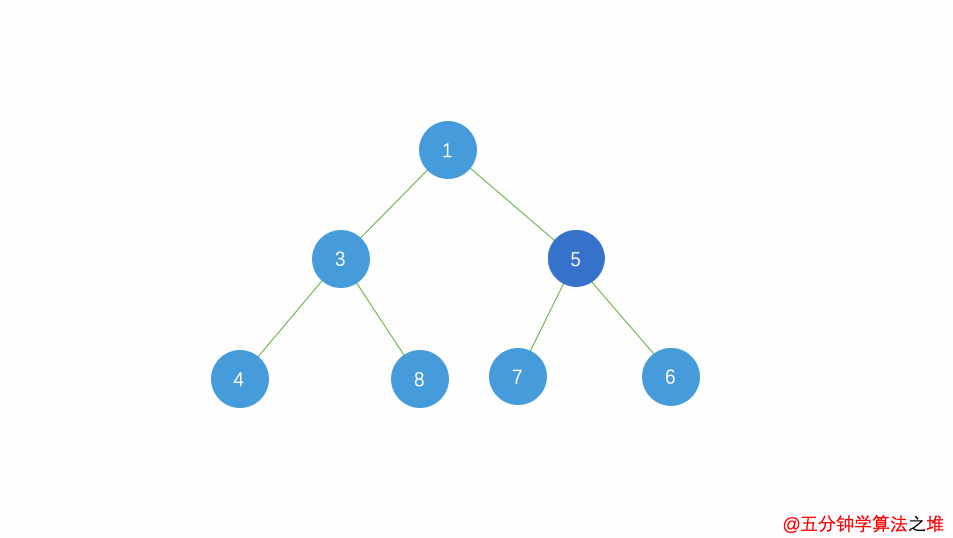
堆的操作：Removemax

按定义，堆中每次都删除第0个数据。为了便于重建堆，实际的操作是将最后一个数据的值赋给根结点，然后再从根结点开始进行一次从上向下的调整。调整时先在左右儿子结点中找最大的，如果父结点比这个最小的子结点还大说明不需要调整了，反之将父结点和它交换后再考虑后面的结点。相当于从根结点将一个数据的“下沉”过程。
小根堆删除动图：

代码：

class HeapSortStudy{

    /**
     * 建堆
     * @param nums
     * @param len
     */
    public static void BuildMaxHeap(int nums[],int len){
        for(int i=len/2-1;i>=0;i--){  //反复调整堆
            AdjustDown(nums,i,len);
        }
    }

    /**
     * 向下调整堆
     * @param nums
     * @param k
     * @param len
     */
    public static void AdjustDown(int nums[],int k,int len){
        //AdjustDown将元素k向下进行调整
        int temp=nums[k];
        for(int i=2*k+1;i<len;i=i*2+1){ //沿k较大的子结点向下筛选，找到最终k所在的位置
            if(i<len-1&&nums[i]<nums[i+1]) i++; //取k较大的子结点的下标（左子结点和右子结点比较）
            if(temp>=nums[i]) break;//当前元素大于左右子结点中最大值，说明不需要调整了，大根堆
//            if(i<len-1&&nums[i]>nums[i+1]) i++; //小根堆
//            if(temp<=nums[i]) break;
            else{  //否则向下进行调整，其实就直接赋值，继续向下筛选
                nums[k]=nums[i]; //将nums[i]调整到双亲结点上
                k=i;//修改k值，以便继续向下筛选
            }
        }
        nums[k]=temp;//将筛选节点的值放到最终位置
    }

    /**
     * 向上调整堆
     * @param nums
     * @param k
     */
    public static void AdjustUp(int nums[],int k){

        int temp=nums[k];
        int i=(k-1)/2; //若结点值大于双亲结点，则将双亲结点向下调，并继续向上比较
        while(i>0&&temp>nums[i]){
            nums[k]=nums[i];//双亲结点下调
            k=i;
            i=(k-1)/2;
        }
        nums[k]=temp;
    }
    /**
    *堆排序步骤为：建立初始堆，由于堆本身特点（堆顶元素就是最大值或者最小值）输出堆顶元素后，将堆底元素送入堆顶，向下调整继
    *续保持大根堆或小根堆的性质，如此重复，直到堆中仅仅剩下一个元素为止。
    */
    public static void HeapSort(int nums[],int len){
        BuildMaxHeap(nums,len);//建堆
        for(int i=len-1;i>0;i--){  //len-1趟交换和调整堆的过程
            //输出堆顶元素（和堆底元素交换）
            Swap(nums,0,i);//每次交换堆顶元素和当前堆底元素
            AdjustDown(nums,0,i);//将剩下的i-1个元素整理成堆
        }
    }
    public static void Swap(int nums[],int a,int b){
        int temp=nums[a];
        nums[a]=nums[b];
        nums[b]=temp;
    }
    /**
     * 插入操作：先将新结点放在堆的末端，再对这个新结点执行向上调整操作。
    */
    public static void insert(int nums[],int k,int num){
        System.out.println("插入元素 "+ num+"之后：");
        nums[k]=num;//插入到堆底
        AdjustUp(nums,k);//向上调整成堆
    }
    /**
    * 删除操作：先将堆的最后一个元素与堆顶元素交换，此时将根结点进行向下调整操作。
    */
    public static void delete(int nums[],int k){ //k为要删除的最后一个元素的索引
        System.out.println("删除堆顶元素"+nums[0]+" 之后：");
        nums[0]=nums[k];//堆底元素替换到堆顶，向下调整成堆
        nums[k]=-1;
        AdjustDown(nums,0,k-1);
    }
    public static void main(String[] args) {
        int nums[]=new int[]{7, 56 ,9 ,7 ,90 ,7 ,0 ,9};
        System.out.println("初始序列为："+Arrays.toString(nums));
        HeapSort(nums,nums.length);
        System.out.println("堆排序之后："+Arrays.toString(nums));

        BuildMaxHeap(nums,nums.length);
        System.out.println("初始建立大根堆："+Arrays.toString(nums));
        delete(nums,nums.length-1);
        System.out.println(Arrays.toString(nums));
        insert(nums,nums.length-1,51);
        System.out.println(Arrays.toString(nums));
    }
}

上面代码输出：

初始序列为：[7, 56, 9, 7, 90, 7, 0, 9]
堆排序之后：[0, 7, 7, 7, 9, 9, 56, 90]
初始建立大根堆：[90, 9, 56, 7, 0, 9, 7, 7]
删除堆顶元素90 之后：
[56, 9, 9, 7, 0, 7, 7, -1]
插入元素 51之后：
[56, 51, 9, 9, 0, 7, 7, 7]

建堆时间为O(n)，之后有n-1次向下调整操作，每次调整时间为O(h)，h为树的高度，因此，堆排序在最好最坏和平均情况下时间复杂度为O(nlogn)。
稳定性方面：在进行筛选时，可能把后面相同的元素调整到前面，所以堆排序是不稳定的。

参考:
1、神级基础排序——堆排序