SVM（一） 拉格朗日乘子法 与 KKT条件

支持向量机（SVM），非常的神秘而众所周知的名字，其出来就受到了很大的追捧，号称最优秀的算法之一，简单地理论构造了复杂的算法，简单地用法实现了复杂的问题，一个词形容就是perfect！

本文旨在从基础出发，实例化的形式一探SVM的究竟。现在网上分析讲解SVM的博文多不胜数，当然对于那些基础好的一看就懂，但对于我这种渣渣来说看一遍也只能浅薄的了解，过两天又忘了公式的缘由。

比如说，在研究SVM之前你是否听过拉格朗日乘子法？是否听过对偶问题？是否了解它们的原理以及如何运用的？还有令人蛋疼的KKT条件了。请问我有没有说到你的心里去啊，但是不用怕，学学就会了。所谓拉格朗日乘子法，大学应该在概率论的点估计中应该学过，但你是否理解了它，如果你那时候理解了，我相信你肯定潜力无限，也不必看我这篇文章了。

1 关于拉格朗日乘子法和KKT条件

1） 关于拉格朗日乘子法 

首先了解一下拉格朗日乘子法，那么我们怎样了解它呢？你只需要记住，有拉格朗日乘子法的地方，肯定会是一个组合优化的问题。带约束的优化问题很好说，比如下面这个问题：

\begin{equation}
\begin{split}
min \ f\ =\ &2x{_1^2}+3x{_2^2}+7x{_3^2} \\
s.t. \ &2x_1 + x_2 = 1 \\
&2x_2 + 3x_3 = 2
\end{split}
\end{equation}

​

这是一个带等式约束的优化问题，有目标值，有约束条件。那么如果假设没有这个约束条件，这个问题该如何求解呢？

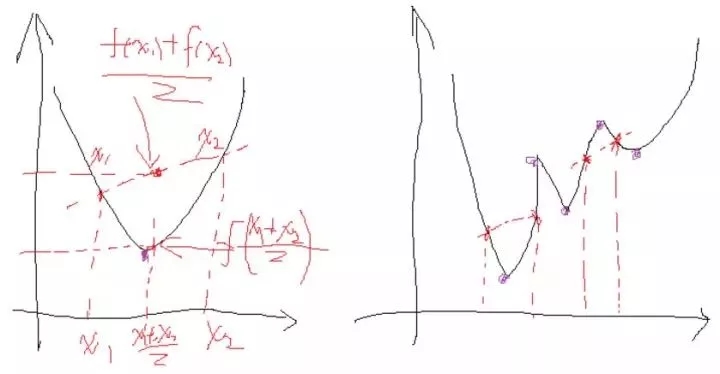
是不是直接f对x求导等于0，解x就可以了，可以看到没有约束的话，求偏导等于0，那么各个x均等于0，这样f=0了。但是x都为0不满足约束条件，那么问题就来了。在这里说一点，为什么上面说求导为0就可以呢？理论上多数问题是可以的，但是有的问题不可以。如果求导为0一定可以的话，那么f就是一个凸优化问题，什么是凸呢，像下面这个左图：

 凸就是开口朝一个方向（向下或者向上）。准确的数学关系就是：

\begin{equation}
\begin{split}
&\frac{f(x_1) + f(x_2)}{2} > f(\frac{x_1+x_2}{2}) \ or \\
&\frac{f(x_1) + f(x_2)}{2} < f(\frac{x_1+x_2}{2})
\end{split}
\end{equation}

​

注意的是这个条件是对函数的任意值x取值。如果满足第一个就是开口向上的凸，反之开口向下的凸。

对于凸问题你可以去求导，从图中可以很容易看出只有一个极点，那么它就是最优点，直观也很合理。类似的看看右边的图，有时候满足第一个关系，有时候满足第二个关系。所以它是一个非凸的问题，对它进行求导会得到很多个极点。

从上图可以看出，只有一个极点是最优解，其他的是局部最优解，那么真实问题时候你选择哪个？所以我们想说的是，拉格朗日乘子法是一定适合于凸问题的，不一定适合其他的问题，还好我们最终的问题是凸问题。

回头再来看看有约束的问题，既然有了约束不能直接求导，那么把约束去掉不就可以了吗。那么怎么去掉呢？拉格朗日大法来了。既然是等式约束，那么就把这个约束乘一个系数加到目标函数里面去，比如上面的函数就变为：

\be