SVM （四） 软间隔和正则化

线性分类SVM面临的问题

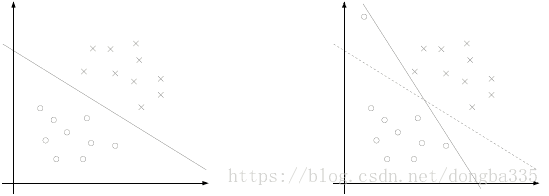
在前面的讨论中，我们一直假定训练样本在样本空间中是线性可分的，存在一个超平面能够把不同类的样本完全划分开。然而，在现实任务中往往是很难找到合适的核函数将训练样本“完全划分”。即使找到了某个核函数刚好将训练集在特征空间中线性可分，但是这种情况也有可能是过拟合造成的。由于噪声值的出现，超平面会有很大的倾斜，会得到一个间隔非常小的超平面，如下图所示。

 

线性分类SVM软间隔最大化

对于上述情况，我们如果仍然希望右图还是虚线的情况（因为这种情况虽然目前分的很好，但是考虑到未来随着数据的增多，最理想的情况仍然是虚线），那我们该怎么办呢？这时我们必须引入“软间隔”概念。左图要求所有的样本必须划分正确，这称之为“硬间隔”。而“软间隔”允许SVM在一些样本上出错，即允许某些样本不满足约束:
\begin{equation}
y_i (W^T x_i + b) \geq 1
\end{equation}

​

 我们原始的问题是
\begin{equation}
\begin{split}
& min \ \frac{1}{2}W^TW \\
 s.t. \ &y_i (W x_i + b) \geq 1, \ i = 1,...,m
\end{split}
\end{equation}

在引入软间隔理论后，我们的优化目标就变成了下面的形式：
\begin{equation}
\begin{split}
& min \ \frac{1}{2}W^TW + C \sum_{i=1}^m \xi_i\\
s.t. \ & y_i (W x_i + b) \geq 1 - \xi_i, \ i = 1,...,m\\
& \xi_i \geq 0,\ i=1,...