机器学习之LDA降维

1. PCA缺点

在上篇介绍PCA的文章中有一句话是:

PCA是一种能够极大提升无监督特征学习速度的数据降维算法

这里很明显的说明,PCA适用于非监督学习的数据降维,显而易见,在进行数据降维的时候,我们并没有考虑数据的类别信息,仅仅是针对数据的特征来进行学习.当已知数据的类别时,在某些情况下,PCA的效果将会非常差.例如:

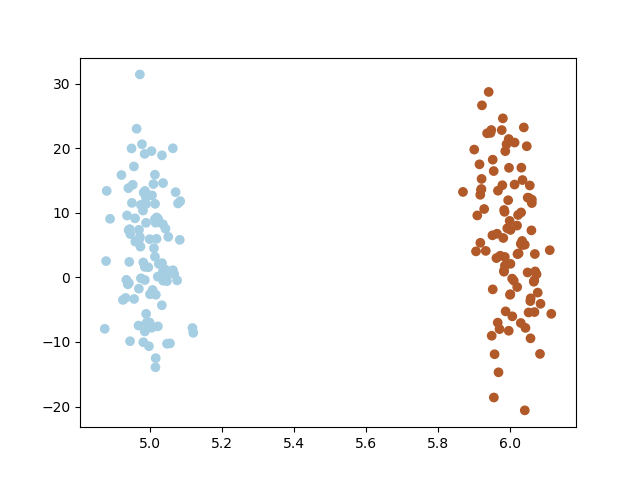
如上图所示,如果使用PCA进行降维,将会映射到Y轴上(接近Y轴,实际的基为[-0.00277403 -0.99999615]),此时数据将变得不可分.如下图所示:

很明显,此时两类数据基本上重叠在一起,无法线性分割.PCA的核心思想是将数据投影到方差最大化的方向,但是方差最大的方向不一定使数据线性可分,PCA之后再使用分类算法将无法获得较好的效果.

2. 线性判别式分析

Fisher’s Linear Discriminant(FLD)和Linear Discriminant Analysis(LDA)是统计学上的经典分析方法,两种不同之处在于LDA比FLD多了一些关于变量分布和协方差的假设.为统一,不再区分FLD和LDA,统称LDA. LDA既可以用来线性分类,也可以用来单纯的对数据进行降维.目前在医学的患者疾病分级,经济学的市场定位,产品管理,市场研究,人脸识别以及机器学习等领域有广泛应用.相较于FLD,LDA假设:
1. 样本数据服从正态分布
2. 各类的协方差相等

虽然这些在实际中不一定满足，但是LDA被证明是非常有效的降维方法，其线性模型对于噪音的鲁棒性效果比较好，不容易过拟合。

2.1 二分类

首先从比较简单的二分类开始,假设存在一组样本数据, 并且分为两个类别:

$$\begin{array}{ll} x &= \{x^{(1)}, x^{(2)}, \cdots, x^{(m)}\} \\ z &\in \{0, 1\} \end{array}$$
如果使用PCA进行降维的话,此时不需要考类别z,但是我们其实是不知道那些被抛弃的不必要特征对分类产生的影响,所以会出现上文中的缺点,丢弃的X轴方向刚好是区分两个类别的方向.

我们的目的是让样本数据能够很好的分成y所代表的的两类,所以,我们只需要将数据映射为一维的,使得数据在一维上能够很好的分开,相同类别的数据聚集在一起,不同类别的数据相互分开即可,此时我们即将数据降低到一维了.那怎么实现这个效果呢?
首先假设这个一维向量为w,映射后的数据:

$$y^{(i)}= w^Tx^{(i)} \quad i \in [1,m]$$
方便起见,假设数据特征数为2,我们的目标就是找到一条直线,样本数据映射其上后,能够最优的分割样本点.如下图:

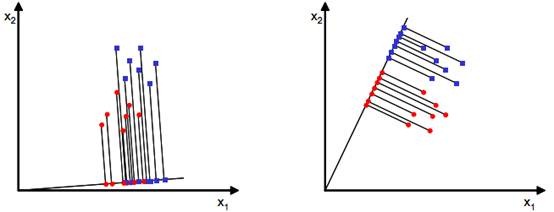
显而易见,右侧的效果更好一点,如何寻找右侧的这条直线,直观上来说,最优分割时,投影后两类样本的均值点相聚最远,假设$N_i$表示对应类别$z_i$的样本数,则原始数据的均值:

$$\mu_i = \frac{1}{N_i} \sum_{x \in z_{i}}x$$
投影之后的均值:
$$\begin{array}{ll} \hat\mu_i &= \frac{1}{N_i}\sum_{x\in z_i}w^T \cdot x \\ \\ &= w^T \cdot u_i \end{array}$$
投影后均值点距离尽量远,表示如下:
$$\begin{array}{ll} J(w) &= |\hat\mu_1 - \hat\mu_2|\\ \\ &= |w^T \cdot (\mu_1 - \mu_2)| \qquad (2.1) \end{array}$$
如果只考虑均值点距离,上述公式2.1越大,越接近最佳效果,事实并非如此,如下图:

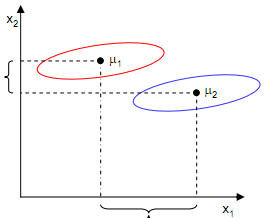
投影到x1轴均值更大,但是分类效果并不好,投影到x2轴则能够更好的分类数据,所以,除了考虑类间均值距离以外,还需要使类内数据尽量的聚集在一起,对于同一个类别内的数据而言,明显x2轴数据比x1轴数据更集中,而判断数据散列程度的度量为方差,考虑投影后类内数据的方差,如下:

$$\begin{array}{ll} \hat S_i &= \sum_{x\in z_i} (w^Tx - \hat u_i)^2 \\ \\ &= \sum_{x\in z_i}(w^Tx - w^T\mu_i)^2 \\ \\ &=\sum_{x\in z_i}(w^Tx - w^T\mu_i)\cdot (w^Tx - w^T\mu_i)^T \\ \\ &= \sum_{x\in z_i}w^T(x - \mu_i)\cdot (x - \mu_i)^Tw \end{array}$$
这里注意 $(w^Tx - w^T\mu_i)$是常数,所以:
$$\begin{array}{ll} (w^Tx - w^T\mu_i)^2 &= (w^Tx - w^T\mu_i)\cdot (w^Tx - w^T\mu_i)^T \\ \\ &= (w^Tx - w^T\mu_i)^T \cdot (w^Tx - w^T\mu_i) \end{array}$$
为了稍后的计算,我们选择前者.定义:

$$S_i = \sum_{x \in z_i}(x - \mu_i)\cdot (x - \mu_i)^T$$

所以:

$$\hat S_i = w^TS_iw$$
我们的目标是: 不同类别的样本点越分开越好，同类的越聚集越好，也就是均值点间距离越大越好，散列值越小越好. 定量表示如下:
$$J(w) = \frac{|\hat\mu_1 - \hat\mu_2|^2}{\hat S_1 + \hat S_2}$$
此时，目标函数值越大，越满足要求，以上公式就定量代表了我们的目标. 带入参数简化上式：
$$\begin{array}{ll} |\hat\mu_1 - \hat\mu_2|^2 &= w^T(\mu_1 - \mu_2)(\mu_1 - \mu_2)^Tw \\ \hat S_1+\hat S_2 &= w^T(S_1 + S_2) w \\ hypothesis \\ S_B &= (\mu_1-\mu_2)(\mu_1 - \mu_2)^T \\ S_W &= S_1 + S_2 \end{array}$$
所以：
$$J(w) = \frac{w^TS_B w}{w^TS_W w}$$
这里有个核心点是：
上述公式，无论w扩大多少倍数，都不会影响最终的结果。所以极值点，w的值并不唯一，此时需要固定w的取值，使：
$$w^TS_Ww=1$$
这不会影响极值点的取值。使用拉格朗日乘子法求解带条件的函数极值：
$$\begin{array}{ll} f(\lambda, w) &= w^TS_Bw + \lambda(1 - w^TS_Ww) \\ \nabla_wf(\lambda, w) &=2S_Bw - 2\lambda S_Ww =0 \\ => & S_Bw=\lambda S_Ww \end{array}$$
求解上述公式的极大值，需要利用矩阵的微积分。假设 $S_W$ 可逆，则：
$$(S_W^{-1}S_B)\cdot w = \lambda w$$
易知，w是 $S_W^{-1}S_B$的特征向量。
进一步带入参数简化：
$$\begin{array}{ll} S_Bw &= (\mu_1 -\mu_2)(\mu_1 - \mu_2)^Tw \\ \\ \lambda_w &= (\mu_1 - \mu_2)^Tw \end{array}$$
这里 $\lambda_w$是一个未知的实数，所以
$$S_W^{-1}S_Bw=S_W^{-1}(\mu_1 - \mu_2)\lambda_w=\lambda w$$ ## 标题 ##
由于w扩大任意倍数都不会影响结果，所以:
$$w=S_W^{-1}(\mu_1 - \mu_2)$$
1. 这里假设 $S_W$可逆，但是当样本维数较高，而样本数较少时，这时可能不可逆，为奇异矩阵。此时可以考虑先使用PCA对样本进行降维，然后再对降维后的数据使用LDA。
2. 求w时，并没有求 $S_W^{-1}S_B$的特征向量，因为不一定是对称矩阵，求它的特征向量时不能使用奇异值分解，使用普通方式求解特征值的方式，时间复杂度为 $O(n^3)$。

2.2 多分类

//todo

参考:
1. https://www.cnblogs.com/engineerLF/p/5393119.html
2. https://www.cnblogs.com/kemaswill/archive/2013/01/27/2879018.html
3. http://blog.csdn.net/zjm750617105/article/details/52104850