来自北大算法课的Leetcode题解：753. 破解保险箱

代码仓库：Github | Leetcode solutions @doubleZ0108 from Peking University.

这题题干描述的非常让人看不懂，非常离谱，还是测试了好几个示例才弄明白的

有一个n位密码，每一位都有k种可能，因为我们并不知道密码，所以所有密码的可能性有$k^n$全排列种，现在要做的就是把这么多可能的密码串成一个，使得最终返回的这一个最短结果每n位都是一个可能的结果，这样用这一个超长的密码一定能把锁打开

最短密码长度一定为 $k^n+(n-1)$ 位

举两个例子：

---

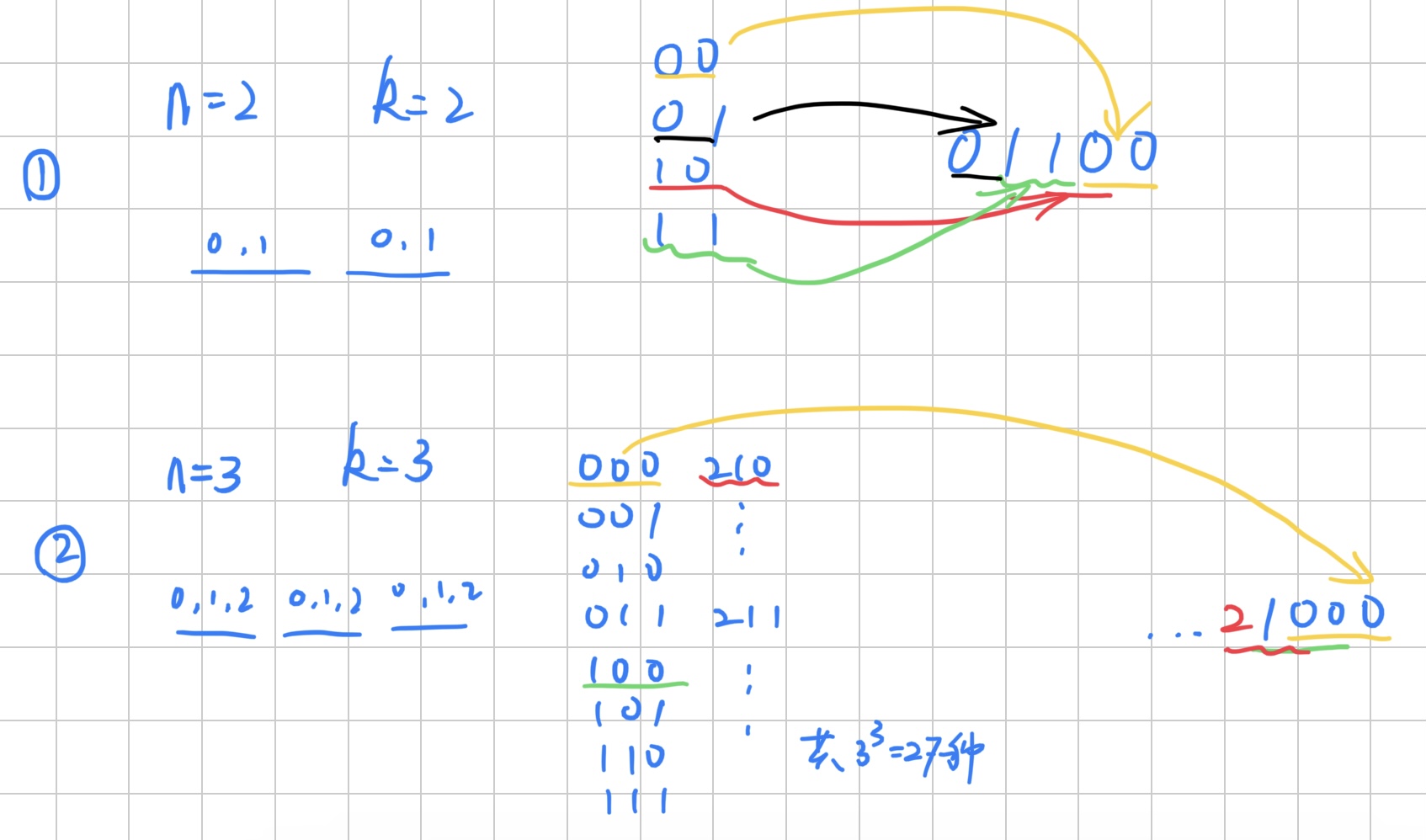
• 解法1: 按照如上图自己在纸上试验的例子，回溯思想两步走：首先先生成$k^n$个全排列，是一个非常经典的组合数问题就不展开了（只提一嘴，这种问题虽然知道所有情况的总个数，但很难用循环法想明白，还是老老实实回溯）；第二步就是模拟彩色箭头的过程，尾部一定是全0字符串（通过几个例子观察的），然后从所有可能的组合中找以当前开头结尾的，拿第二个例子来说，找末尾是00的，比如100，它可以作为串接上，接下来开头变成10，210可以继续接上，需要注意并不是能接上就一定能成为最终答案，可能接到一半后面就再也接不动了，那这种情况就要被pass，明显是回溯到思想不断尝试，每尝试一个，就在所有排列中删除这种可能，直到总密码长度够长
  • 改进1(超时 27/38)：因为回溯法通过不断递归目标是找到所有可能的解，但本问题只需要选择第一个解，因此不需要回溯所有可能解，我们让找到解后返回True，在根的调用时不直接调用，而是放在一个if里调用，如果能成则直接返回不继续递归
  • 改进2(超时 29/38)：添加visited集，有很多中间子串是不能成为最终密码的，因为他们不能继续往前接，所以添加一个visited，如果某次递归处理过当前串了就没必要继续处理了
  • 改进3(T13% S6%)：仔细想，其实没有必要先把所有全排列生成了，因为后面的回溯里都是一位一位往串上加的，也是收到解法二的启示，只能从k往前遍历，把新的字符加到当前的尾部，整体思路跟解法2很像，只是用回溯的递归框架实现
• 解法2(T29% S92%)：BFS，问题的本质就是给定一个全0串后，不断的往前（或往后）加一位再加一位，最终把所有可能的全排列都用完了也就组成了全能密码，因此我们还是同样的使用一个visited集，从k-1往前试探，去掉n位密码的第一位，再补上一个新的位，如果这种排列志气那没遇到，则证明可以继续往前发展，所以最终结果也可以添加这位。深度优先搜索本来就是找到一个可能的解就得了，因此不用担心结果一直不断的加，只要能把所有排列恰好用光，那一定是可能的解

为什么只能从k往前遍历，从0开始往后会遇到某个排列之前用过的情况，导致无法给出答案

class Solution:
    # 解法1 改进3
    def crackSafe(self, n: int, k: int) -> str:
        visited = set(["0"*n])

        def combine(parts, res):
            if len(res) == k**n+n-1:
                return res

            for i in range(k-1, -1, -1):
                if (parts[1:]+str(i)) not in visited:
                    visited.add(parts[1:]+str(i))
                    return combine(parts[1:]+str(i), res+str(i))

        res = combine("0"*n, "0"*n)
        return res

    # 解法2
    def crackSafe2(self, n: int, k: int) -> str:
        queue = deque(["0"*n])
        visited = set(["0"*n])
        res = "0"*n

        while queue:
            parts = queue.popleft()
            for i in range(k-1, -1, -1):
                parts_ = parts[1:] + str(i)
                if parts_ not in visited:
                    visited.add(parts_)
                    queue.append(parts_)
                    res += str(i)
                    break
        return res

    # 解法1 超时
    def crackSafe1(self, n: int, k: int) -> str:
        perms = set()
        def getPerm(parts):
            if len(parts) == n:
                perms.add(parts)
                return
            for i in range(k):
                getPerm(parts + str(i))
        getPerm("")
        

        res = []
        visited = set()
        def combine(parts, perms_remain):
            if len(parts) == k**n+n-1:
                res.append(parts)
                return True     # 改进1

            visited.add(parts)

            for item in perms_remain:
                if item.endswith(parts[0:n-1]) and not (item[0] + parts) in visited:
                    if combine(item[0] + parts, perms_remain - set([item])):
                        return True     # 改进1

        combine("0"*n, perms-set(["0"*n]))
        return res[0]