电路(第三章、线性直流电路一般分析方法)

1.线性直流电路的一般分析方法

1). 支路电流法

2). 回路电流法

3). 节点电压法

1). 支路电流法
a. 2b法，对于一个具有n个节点，b条支路的电路独立方程个数
KCL：n-1
KVL：b-n+1
支路方程：b
上述方程可以解出所有电压电流。
b.支路电流法
设给定的线性直流电路具有b条支路，n个节点，那么支路电流法就是以b个未知的支路电流作为待求量，对n-1个节点列出独立的KCL方程，在对b-n+1个回路列出独立的KVL方程，这b个方程联立便可解得b个支路电流。
$关键：独立方程的列写$
$KCL方程：n-1$
$KVL方程：b-n+1(选网孔，网孔数等于独立方程数)$、

2). 回路电流法
a.回路电流：假设在每个独立回路中闭合流动的电流。
b.回路电流法：以回路电流作为待求量，对b-n+1个回路列写KVL方程的方法。
c.列些规则：如上图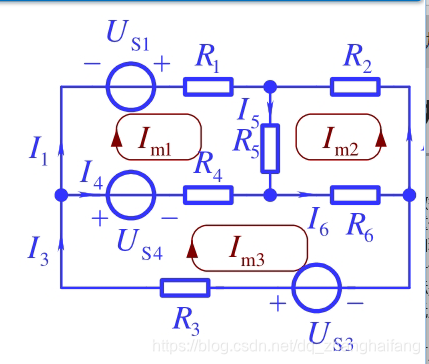
$$R_{11}{I}_{m1}+R_{12}{I}_{m2}+R_{13}{I}_{m3}=\sum _{回路1}{U}_s$$
$$R_{21}{I}_{m1}+R_{22}{I}_{m2}+R_{23}{I}_{m3}=\sum _{回路2}{U}_s$$
$$R_{31}{I}_{m1}+R_{32}{I}_{m2}+R_{33}{I}_{m3}=\sum _{回路3}{U}_s$$
(1). R 11 = R 1 + R 4 + R 5 , R 22 = R 2 + R 5 + R 6 , R 33 = R 3 + R 4 + R 6 \color{blue}R_{11}=R_1+R_4+R_5,R_{22}=R_2+R_5+R_6,R_{33}=R_3+R_4+R_6 R11​=R1​+R