第六章、正弦稳态电路分析

一、正弦电路的分析
标准直流：大小和方向均不随时间改变的恒定信号
交流：大小和方向都随时间做周期性变化的信号
二、正弦信号的三要素
随时间按正弦规律变动的电流称为正弦电流。
$i=I_{m}cos(wt+{\psi }_i)$

$I_m$:振幅或幅值
${\psi }_i$:初项，一般$|{\psi }_i|<\pi$,与计时起点有关
$w$:角频率,$w=\frac{2\pi }{T}=2\pi f$
即，幅值，初项，角频率称为正弦信号的三要素。
三、我国标准频率为50Hz，称为工频，$w=100\pi rad/s$。
电网频率：美国和台湾为60Hz
人耳可以听见的声音频率约在 20 ~ 20000 Hz
移动通信频率：900MHz~1800 MHz
无线通信频率： 高达 300GHz
四、正弦电路常见概念
1、参考正弦量：图示电压$u$通过最大值的瞬间作为时间坐标原点（t=0），此时${\psi }_u=0$，正弦电压为$u=U_{m}coswt$，$i=I_{m}cos(wt+{\psi }_i)$

2、有效值：与交流热效应相等的直流量定义为交流电 的有效值，是瞬时值在一个周期内方均根值$$I=\sqrt{\frac{1}{T}{\int }_0^T{i}^{2}dt}=\frac{I_m}{\sqrt{2}}$$
注意：
交流电压、电流表测量数据为有效值；
交流设备名牌标注的电压、电流均为有效值。
3、相位差：同频率正弦电压$u=U_{m}cos(wt+{\psi }_u)$和正选电流$i=I_{m}cos(wt+{\psi }_i)$的相位差，$\varphi ={\psi }_u-{\psi }_i$
注意：
~两同频率的正弦量之间相位差为常数，与计时起点无关。
~不同频率的正弦量比较无意义。

五、复数表示法
1、设A是一个复数，可表示为 直角坐标式 $A=a+jb$
极坐标式：$A=|A|e^{j\theta }$，简写：$A=|A|\angle \theta$
$a=|A|cos\theta ，b=|A|sin\theta ,\theta =arctan\frac{b}{a}$


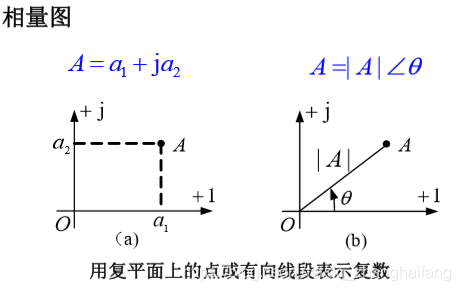
正弦量的相量表示：$f(t)=A_{m}cos(wt+\psi )$
由欧拉公式得：$\acute{A_m}=A_m{e}^{j\psi }=A_m\angle \psi$

注：
~相量只是表示正弦量，而不等于正弦量
~只有正弦量才能用相量表示，非正弦量不能
~只有同频率的正弦量才能画在同一相量图上
~相量的两种表示形式 ，直坐标，极坐标


六、相量运算规则
1、唯一性：两个同频率正弦量相等的充要条件是代表这两个正弦量的相量 相等。即对于所有的时间 t ，$Re[{\acute{A}}_{1m}{e}^{jwt}]=Re[{\acute{A}}_{2m}{e}^{jwt}]$充要条件${\acute{A}}_{1m}={\acute{A}}_{2m}$
2、线性性质：N个同频率正弦量线性组合(具有实系数)的相量等于各个 正弦量相量的同样的线性组合。设 $f_k(t)=Re[{\acute{A}}_{mk}{e}^{jwt}]$则$$\sum _{k=1}^N{b}_k\ast f_k(t)\iff \sum _{k=1}^N{b}_k\ast {\acute{A}}_{mk}$$
3、微分规则：正弦量(角频率为ω) 时间导数的相量等于表示原正弦量的相 量乘以因子 $j\omega$
即：$\frac{d}{dt}f(t)\iff jw{\acute{A}}_m$
4、积分规则：正弦量(角频率为ω) 时间积分的相量等于表示原正弦量的相 量除以因子$j\omega$。

七、 基尔霍夫定律相量形式


八、RLC 各元件伏安特性相量形式






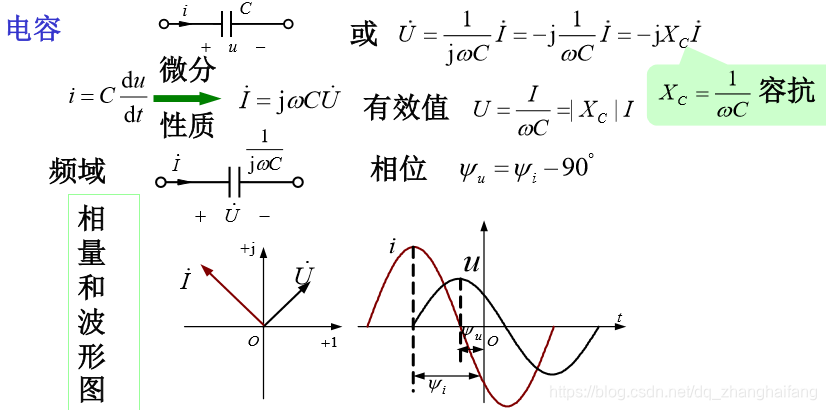
九、阻抗和导纳






导纳







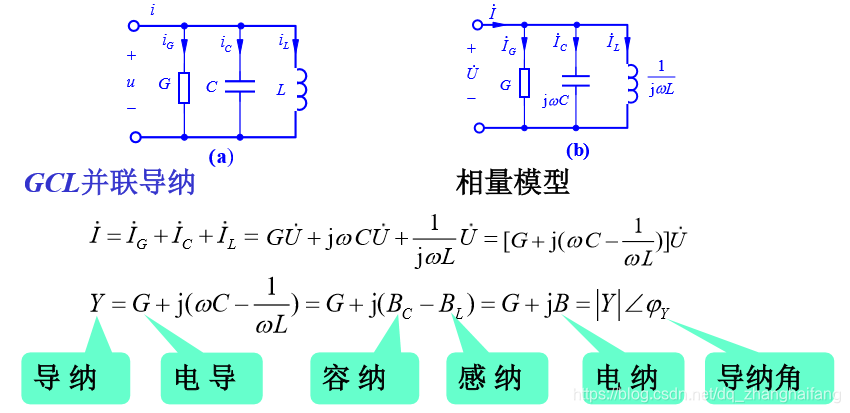
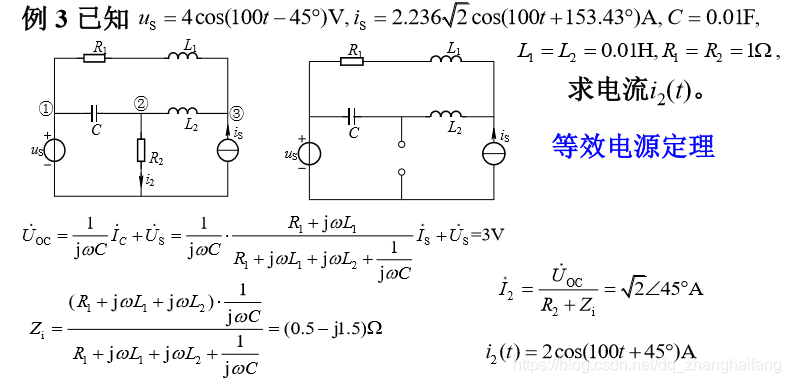
十、正弦交流含独立源一端口网络如图 (a)所示