chapter 3 POTENTIAL VORTICITY THINKING AND ROSSBY WAVE DYNAMICS

3.1 Fundamental aspects of QGPV

3.1.1 Relationship with Ertel PV

QGPV（准地转势涡度）的守恒方程可以通过Ertel PV的物质守恒直接推导出来。Ertel PV的定义为：
$$P=\frac{1}{\rho }\zeta \cdot \nabla \theta$$
其中，$\rho$为密度，$\zeta$为涡度，$\nabla \theta$为位温的梯度。根据Hoskins和James（2014）中的完整三维流动理论（第12.4节），这一守恒方程可以表示为：
$$\left(\frac{\partial }{\partial t}+\mathbf{V}\cdot \nabla +w\frac{\partial }{\partial z}\right)P\approx \left(\frac{\partial }{\partial t}+\mathbf{V}\cdot \nabla \right)\left\{\left(\frac{f_0}{{\rho }_r}\frac{d{\theta }_r}{dz}\right)\frac{q}{f_0}\right\}\approx 0$$
这一式子中，应用了准地转（QG）尺度假设，即$Fr\sim Ro\ll 1$，并保留了一阶近似项。这里的关键区别在于：
1. QGPV的守恒：在每一高度（或压力坐标系下的压力面）上，QGPV遵循水平流动的守恒。
2. Ertel PV的守恒：Ertel PV在完整的三维流动中（如果是绝热的，则沿等位温面）守恒。
在QGPV方程（$\frac{D_{g}q}{Dt}=0$）中，输运速度也被近似为地转风（这一点与$Ro\ll 1$假设一致）。需要注意的是，QGPV并不是对Ertel PV的完全近似，两者具有不同的单位。

3.1.2 QGPV的反演（Inversion of QGPV）

我们是否可以直接用Ertel PV描述动力学，而不需要进一步推导QGPV？答案在于QGPV与地转流函数（geostrophic streamfunction）及地转风的关系。这引出了与PV异常相关的两个重要概念：可反演性（invertibility）和远距作用（action-at-a-distance）。

QGPV扰动的定义：

QGPV扰动的定义为：
$$q^{\prime }=q-f={\nabla }_h^2{\psi }_g+f_0^2\frac{\partial }{\partial z}\left(\frac{1}{N^2}\frac{\partial {\psi }_g}{\partial z}\right)=\mathcal{L}{\psi }_g$$

其中，${\psi }_g$为流函数，$\mathcal{L}$为作用于流函数的微分算子。该方程仅涉及流函数的导数，其系数仅依赖于参考状态（$f_0,N(z)$）。理论上，通过合适的边界条件，方程可以数学上反演（即积分），得到：
$${\psi }_g={\mathcal{L}}^{-1}{q}^{\prime }$$
利用地转平衡和静力平衡，还可以计算地转风速和浮力：
$$u_g=-\frac{\partial {\psi }_g}{\partial y},v_g=\frac{\partial {\psi }_g}{\partial x},b^{\prime }=f_0\frac{\partial {\psi }_g}{\partial z}$$
假设$N^2$为常数，并重新定义高度坐标为$\hat{z}=(N/f_0)z$(这样就可以把psi写成nabla的形式了)，可以简化为：
$$q^{\prime }\approx \left(\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}+\frac{{\partial }^2}{\partial {\hat{z}}^2}\right){\psi }_g={\nabla }^2{\psi }_g$$

PV异常的远距作用（PV ball）???

$$q^{\prime }\approx {\nabla }^2{\psi }_g\approx {\xi }_g$$
PV异常既有环流效应，也有温度异常。例如：
• 当$q\prime >0$时，产生反气旋方向的环流；
• 当$q\prime <0$时，产生气旋方向的环流。

PV的远距作用类似于电荷通过电场对远处的电荷产生作用。PV异常通过诱导的流函数${\psi }_g$影响远处的流场，从而对大范围大气现象产生影响。

图 4a表示在高空有正位涡异常区的情况下，由于在正位涡异常区内位涡比周围高，即是一个涡度和静力稳定度大值区，因此在正位涡异常区内等位温面向正位涡异常中心收拢，造成与在正位涡异常中心的上方和下方相邻的等熵面之间的距离拉大，致使那里的静力稳定度减小。由于位涡守恒性的作用，使气旋性涡度增大，结果便出现围绕正位涡异常区的气旋性环流。
图 4b表示在高空有负位涡异常区的情况下，与上述情况相反, 由于在负位涡异常区内位涡比周围低，即为一个涡度和静力稳定度小值区，因此在负位涡异常区内等位温面向负位涡异常中心分开，造成与在负位涡异常中心的上方和下方相邻的等熵面之间的距离缩短，致使那里的静力稳定度增大, 气旋性涡度减小, 反气旋性增大，结果便出现围绕负位涡异常区的反气旋性环流。

$$q^{\prime }={\nabla }_h^2{\psi }_g+f_0\frac{\partial }{\partial z}\left(\frac{b^{\prime }}{N^2}\right)$$
图 4c表示在位涡均匀分布的低层有正温度异常出现的情况下，各等熵面间的间隔加大，使静力稳定度减小，因而气旋性涡度增大，结果便出现围绕正温度异常区的气旋性环流。类似地, 在低层有负温度异常出现的情况下，各等熵面间的间隔减小，使静力稳定度增大，因而引起反气旋性涡度增大，结果便出现围绕负温度异常区的反气旋性环流(如图 4d所示)。上述等熵位涡思想也可通过图 5得到清楚的表示。

示意图说明：

图12展示了单独正PV球产生的诱导异常：
• 在垂直方向上，浮力梯度（$b^{\prime }/\partial z$）或静力稳定性在正PV异常上方增加，在其下方减少；
• 环绕正PV异常的等位温面仅略微扰动。

3.1.3 Inversion of boundary thermal anomalies

在大气动力学中，潜势涡度 (PV) 异常通常被认为是远离边界发生的。然而，如果位温异常集中在地面附近，这将导致地转流函数（${\psi }_g$）发生变化，并随着高度逐渐衰减。
静力平衡与边界条件
根据静力平衡条件，边界上的关系为：
$$f_0\frac{\partial {\psi }_g}{\partial z}=b^{\prime },$$
其中，$b^{\prime }$ 表示浮力扰动。如果边界上有一个暖的正浮力扰动（即 $b^{\prime }>0$），意味着在地表附近的流函数具有以下特性：$f_0\frac{\partial {\psi }_g}{\partial z}>0$

对于暖的正 $b^{\prime }$ 异常，我们假设其诱导的流动在远离地面的高度（$z\to \infty$）时趋于零，即${\psi }_g\to 0$。结合边界的条件($f_0{\psi }_g(z=0)<0$)，可以得出暖异常会引发气旋式环流，并随着距离增加而衰减。
在北半球，由于 $f_0>0$，暖异常诱导的流函数${\psi }_g$具有正的涡度 (${\xi }_g>0$)，旋转方向为逆时针。
对于孤立的冷异常（即$b^{\prime }<0$），与暖异常相反，它会引发反气旋式环流。地表的流函数值为正（$f_0{\psi }_g(z=0)>0$），并且其诱导的涡度为负 (${\xi }_g<0$)，旋转方向为顺时针。
热力异常与PV异常的相互作用
边界热异常与对流层上层的PV异常相互作用，对天气系统的发展有显著影响：
1. 高层PV异常通过地转风影响地面附近的温度分布，从而对边界热异常产生影响；
2. 边界热异常通过感热输送和对流，影响高层PV异常的传播。
当两者的相互作用导致不稳定性时，会形成斜压不稳定（Baroclinic Instability），这是一种促进天气系统发展的机制。

3.2 Rossby waves

3.2.1 Wave propagation

罗斯贝波的传播可以通过对基本状态的线性化分析来理解。在准地转理论 (QG) 框架下，潜势涡度沿水平面输送。假设基本状态流动为一个稳定的纬向流 $\bar{u}(y,z)$ ，总 PV 表示为：

$$q=\bar{q}(y,z)+q\prime (x,y,z,t),$$

其中 $\bar{q}$ 是基本状态 PV， $q\prime$ 是扰动 PV。

PV 方程线性化后为：

$$\left(\frac{\partial }{\partial t}+\bar{u}\frac{\partial }{\partial x}\right)q\prime +v\prime \frac{\partial \bar{q}}{\partial y}=0.$$
该方程表明，PV 扰动 $q\prime$ 的演化受纬向基本流的输运以及经向 PV 梯度 $\frac{\partial \bar{q}}{\partial y}$的影响。

推导
QGPV 的守恒方程为：
$$\frac{\partial q}{\partial t}+\mathbf{V}\cdot \nabla q=0,$$
同时，水平速度也可以分解为：
$$u=\bar{u}(y,z)+u^{\prime }(x,y,z,t),v=v^{\prime }(x,y,z,t),$$
将 $q=\bar{q}+q\prime$ 和速度分解代入原始 QGPV 方程：
$$\frac{\partial (\bar{q}+q\prime )}{\partial t}+(\bar{\mathbf{V}}+\mathbf{V}\prime )\cdot \nabla (\bar{q}+q\prime )=0,$$
其中 $\bar{\mathbf{V}}=(\bar{u},0)$ 是基本状态流。
展开后得到：
$$\frac{\partial \bar{q}}{\partial t}+\frac{\partial q\prime }{\partial t}+\bar{\mathbf{V}}\cdot \nabla \bar{q}+\bar{\mathbf{V}}\cdot \nabla q\prime +\mathbf{V}\prime \cdot \nabla \bar{q}+\mathbf{V}\prime \cdot \nabla q\prime =0.$$
线性化过程中，忽略高阶小扰动项（即 $\mathbf{V}\prime \cdot \nabla q\prime$），基本状态流不随时间变化，得到：
$$\frac{\partial q\prime }{\partial t}+\bar{\mathbf{V}}\cdot \nabla q\prime +\mathbf{V}\prime \cdot \nabla \bar{q}=0.$$

罗斯贝波的相速度
假设波动以波数 k 和频率 $\omega$ 沿 x 方向传播：
$$q\prime =q_k{e}^{i(kx-\omega t)}.$$
通过准地转反演关系 $q\prime \sim {\nabla }^2\psi \prime$ ，流函数扰动可以表示为：
$$\psi \prime =-{\psi }_k{e}^{i(kx-\omega t)}.$$
将以上表达式代入 PV 方程，得到相速度 c 的色散关系：
$$c=\frac{\omega }{k}=\bar{u}-\frac{{\psi }_k}{q_k}\frac{\partial \bar{q}}{\partial y}.$$
罗斯贝波的相速度由两部分组成：
1. 平流效应：由基本纬向流 $\bar{u}$ 决定；
2. 波动传播：与 PV 梯度 $\frac{\partial \bar{q}}{\partial y}$ 和扰动幅度 $\frac{{\psi }_k}{q_k}$ 相关。

当经向 PV 梯度为正时，波动通常向西传播（即负的 x 方向），与盛行西风相反。
行星波的特性
行星波（罗斯贝波的一种）由于地球行星涡度随纬度变化（$\beta$）而存在。其色散关系为：
$$c=\bar{u}-\frac{\beta }{k^2+l^2},$$
其中 k 和 l 分别是纬向和经向波数。
• 长波（小 k ）：传播速度更快，易向西传播；
• 短波（大 k ）：传播速度较慢。
若基本流为西风，长波可能停滞于地面（即 c = 0 ）。

3.2.2 物理传播机制

图示 (Fig. 16) 展示了行星罗斯贝波的机制：
• 在正的经向 PV 梯度 $\frac{\partial \bar{q}}{\partial y}>0$ 区域，南向气团携带较高 PV 形成正 PV 异常；北向气团携带较低 PV 形成负 PV 异常。
• 正 PV 异常引发气旋式环流，拉动等 PV 线南移；负 PV 异常引发反气旋式环流，拉动等 PV 线北移。
• 总体结果是波动向西传播。

3.3 Boundary temperature waves and surface QG dynamics

3.3.1 Propagation

在本节中，我们考虑一种状态：纬向风随高度的线性切变，并且在热力平衡下温度随纬度向极地递减。对于这种背景状态，其热力平衡条件为：

$\frac{\partial \bar{u}}{\partial z}=\Lambda =-\frac{1}{f_0}\frac{\partial \bar{b}}{\partial y},$

其中：
• $\bar{u}$ 是纬向基本流；
• $\bar{b}$ 是背景浮力。

假设基本状态的 PV 梯度为零（$\frac{\partial \bar{q}}{\partial y}=0$），因此罗斯贝波无法在流体内部传播。但在地表，由于垂直速度 w = 0 ，线性化的热力学方程为：

$$\left(\frac{\partial }{\partial t}+\bar{u}\frac{\partial }{\partial x}\right)b\prime +v\prime \frac{\partial \bar{b}}{\partial y}=0,$$

其中：
• $b\prime$ 是浮力扰动；
• $v\prime$ 是扰动的经向风速。

温暖的浮力异常（正 $b\prime$ ）会诱导气旋式环流，冷的浮力异常（负 $b\prime$）会诱导反气旋式环流。假设浮力波表现为：
$$b\prime =b_k{e}^{ikx},$$
浮力波会伴随地表经向风的变化向东传播。
边界罗斯贝波的传播
由于地表的经向浮力梯度为负 ($-\partial \bar{b}/\partial y<0$)，浮力波相对于地表流动向东传播。这种波动被称为边界罗斯贝波，它沿地表温度梯度传播。

通过求解边界条件得到流函数扰动的表达式：
$$\psi \prime ={\psi }_k{e}^{ikx}{e}^{-Nz/f_0}{e}^{-i\omega t},$$
其 e -折减高度由罗斯贝高度尺度决定：
$$h=\frac{f_0}{Nk}.$$
进一步代入热力学方程，可以得到边界罗斯贝波的相速度：
$$c=\frac{\omega }{k}=\bar{u}-\frac{{\psi }_k}{b_k}\frac{\partial \bar{b}}{\partial y}=\bar{u}-\frac{f_0\Lambda }{Nk}.$$
由于地表温度梯度为负，相速度为正，即波向东传播。

3.3.2 PV反演的尺度效应

内部 PV 异常的尺度效应：
长波（波数 k 小）会引发更强的流函数扰动，这是因为：
$$\frac{\psi \prime }{q\prime }\sim \frac{1}{k^2}.$$
这表明：
1. 大尺度 PV 特征对流动的影响更显著；
2. PV 反演算子更偏向长波分量，使 PV 的分布表现为平滑的波动。
边界浮力异常的尺度效应：
边界浮力异常引发的流函数扰动与其波长有关：
$$\frac{\psi \prime }{b\prime }\sim \frac{1}{Nk}.$$
尽管这种效应不如内部 PV 异常显著，但对于小尺度浮力异常，其对局地流动的影响更为突出。

3.4 Shear instability and the Rayleigh model

3.4.1 基本状态 (The Basic State)

在流体动力学中，速度随空间平滑变化的单向流动被称为层流 (laminar flow)。然而，层流中如果存在速度剪切 (shear)，常常会变得不稳定，这意味着微小的扰动可能会迅速增长，最终破坏层流结构，导致湍流 (turbulent flow)。

雷利 (Lord Rayleigh) 于 1880 年首次提出了剪切不稳定性的理论，并使用了一个简单的模型进行解释。这一模型描述了：
• 一个均匀向右流动的流体层；
• 与一个均匀向左流动的流体层分隔开，两层之间有一条速度线性变化的剪切带。

这一状态被称为雷利模型 (Rayleigh Model)。

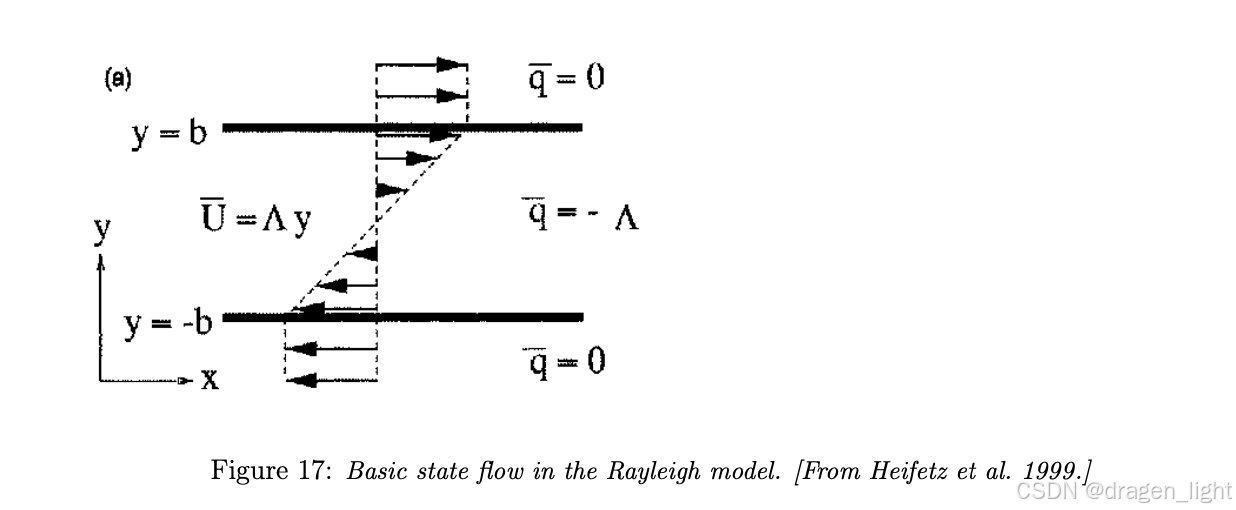
数学描述

基本流动的速度分布 $\bar{u}$ 可以表示为：
$$\bar{u}=\{\begin{array}{ll}U,& y>b,\\ \Lambda y,& -b<y<b,\\ -U,& y<-b,\end{array}$$
其中：
• U 是上下流体层的均匀流速；
• $\Lambda =U/b$ 是剪切速率；
• b 是剪切带的半宽度。

剪切带 (-b < y < b) 内速度线性变化，而剪切带外速度为常数。
潜势涡度的分布 ($\bar{q}=\zeta =-\Lambda$)
在该模型中：
1. 剪切带外 ( y > b 或 y < -b )：
• 速度均匀，涡度梯度为零；
• 潜势涡度 $\bar{q}$= 0 。
2. 剪切带内 (-b < y < b)：
• 存在速度梯度，涡度为负，$\bar{q}=-\Lambda$。
3. 剪切带边界 ( $y=\pm b$ )：
• 剪切带边界处潜势涡度发生跃变，形成类似 $\delta -$函数的 PV 梯度尖峰。

3.4.2 Wave Interaction and Phase-Locking

在雷利模型中，潜势涡度 (PV) 的边界处存在波动扰动，这些扰动引发了波的传播。然而，由于剪切的存在，这些波动表现为反向传播罗斯贝波 (Counter-Propagating Rossby Waves, CRWs)，它们在两个边界上相对基本流向相反的方向传播。

1. 波动传播机制
   假设 y = b 处的空气发生波动偏移，由罗斯贝波机制，这一波动将在正的 PV 梯度上向负 x 方向传播。而 y = -b 处的波动则因 PV 梯度为负，将相对流动向正 x 方向传播。结果是：
   • 每个波都在剪切带的边界上沿相对方向传播；
   • 剪切作用试图抵消波的相对运动，形成一种相互耦合的反向传播波。
2. 远程作用与相互影响
   尽管波动的 PV 异常主要集中在剪切带的边界，但由于 PV 反演的远程作用 (Action-at-a-Distance) 属性，这些波动会通过其诱导的流动影响另一边界上的波动。例如：
   • y = -b 处波动诱导的流场能够推动 y = b 处的 PV 异常；
   • y = b 处波动的流场同样作用于 y = -b 处，影响其传播。
   这种远程相互作用形成了两个波之间的耦合，并对它们的传播产生关键影响。
3. 图解说明

   1. 图 18：反向传播罗斯贝波
      • 展示了剪切带边界上的 PV 波动及其传播方向；
      • 虚线箭头表示远程作用下的诱导流动，固线箭头显示波动的实际传播方向。
      

   2. 图 19：相位差的影响
      • 描述了波动相位差对其相互作用的影响：
      • $0<ϵ<\pi /2$ ：波动相互促进，传播增强；
      • $\pi /2<ϵ<\pi$ ：波动相互削弱，传播受阻。

最终，相位差趋于相位锁定，波动以相同速度共同传播。

3.4.3 Evolution of wave amplitudes and phases

在前文中，通过物理解释，我们理解了两边界上的反向传播罗斯贝波 (CRWs) 是如何相互作用以改变传播速度和幅度的。这一过程可以用数学方法描述，通过将潜势涡度 (PV) 和流函数的扰动表示为两波叠加的形式。
1. CRWs 的数学表达
假设两个 CRWs 的扰动分别为 q_1 和 q_2，总的潜势涡度扰动可以写作：
$$q\prime =\left\{a_1{e}^{i{ϵ}_1}{q}_1+a_2{e}^{i{ϵ}_2}{q}_2\right\}{e}^{ikx},$$
其中：
• $a_1$, $a_2$ 分别是两波的振幅；
• ${ϵ}_1$, ${ϵ}_2$ 是相位；
• k 是波数。
对应的流函数扰动为：
$$\psi \prime =-\left\{a_1{e}^{i{ϵ}_1}{\psi }_1+a_2{e}^{i{ϵ}_2}{\psi }_2\right\}{e}^{ikx}.$$
2. 振幅与相位的演化方程
将上述表达式代入线性化的潜势涡度方程后，可以得到振幅和相位的演化方程。对于第一个波 ($q_1$)，我们有：
1. 振幅的演化：
$$\frac{1}{a_1}\frac{d{a}_1}{dt}=\frac{-a_2}{a_1}{\gamma }_2^1\sin ϵ,$$
其中 $ϵ={ϵ}_2-{ϵ}_1$ 是两波的相位差，${\gamma }_2^1$ 是相互作用系数。
2. 相位的演化：
$$\frac{d{ϵ}_1}{dt}=-k{c}_1+{\gamma }_1^1+\frac{a_2}{a_1}{\gamma }_2^1\cos ϵ.$$
类似地，对于第二个波 (q_2)：
1. 振幅的演化：
$$\frac{1}{a_2}\frac{d{a}_2}{dt}=\frac{a_1}{a_2}{\gamma }_1^2\sin ϵ.$$
2. 相位的演化：
$$\frac{d{ϵ}_2}{dt}=-k{c}_2+{\gamma }_2^2+\frac{a_1}{a_2}{\gamma }_1^2\cos ϵ.$$
3. 相互作用系数的意义
相互作用系数 ${\gamma }_j^i$ 定义为：
$${\gamma }_j^i=\frac{k{\psi }_j\frac{\partial q_j}{\partial y}}{q_j},$$
表示波 j 在另一波 i 的诱导流场中的传播效应。这些系数量化了两波通过远程作用耦合的强度。
4. 正常模增长与相位锁定
当两波达到稳定相互作用时，形成所谓的相位锁定状态 (Phase-Locked Configuration)。在这种状态下：
1. 两波的振幅以相同速率增长：
$$\frac{1}{a}\frac{da}{dt}=\sigma \sin ϵ,$$
其中 $\sigma$ 是总的相互作用强度。
2. 相速度相等，波以相同的传播速度传播。

图 20 展示了不同波数下 CRWs 的相位差、增长率以及传播速度的变化：
1. 波数较小时，两波可以实现相位锁定并达到较高的增长率；
2. 波数较大时，相互作用减弱，波无法保持相位锁定。

3.4.4 最优增长

尽管短波（波长短）无法实现相位锁定，CRWs 在某些条件下可以达到最优增长：
• 在相位差 $ϵ=\pi /2$ 附近，增长率达到峰值。
• 这种短暂的快速增长为天气系统中的涡度发展提供了动力学机制。

3.5 Baroclinic instability

3.5.1 General argument for baroclinic growth

1. 斜压与斜压不稳定性

斜压性 (Baroclinicity) 是指大气中等压面和等密面（或等位温面）不平行的现象，这种状态下，水平温度梯度存在并驱动了垂直方向的风切变。

斜压不稳定性 是一种依赖于垂直方向剪切层中波动相互作用的不稳定性，通常发生在两个垂直层上潜势涡度 (PV) 梯度相反的情况下：
• 上层：正 PV 梯度 ($q_y$ > 0)；
• 下层：负 PV 梯度 ($q_y$ < 0)。

2. 斜压不稳定性的物理机制

斜压不稳定性是由两个垂直层之间的反向传播罗斯贝波 (CRWs) 的相互作用驱动的。这与水平流剪切中的斜压不稳定性（Barotropic Instability）相似，但关键区别在于：
1. 波动的相对位置：
• 斜压不稳定性：波动在垂直方向上分离（即不同高度）；
• 斜压不稳定性：波动在水平方向上分离（即不同纬度）。
2. 波的传播方向：
• 在斜压不稳定性中，上层的罗斯贝波沿西向传播，而下层波沿东向传播，两者传播方向相反。
3. 反向传播罗斯贝波的相互作用
在斜压不稳定性中，上下层的 CRWs 相互作用，形成了以下特性：
1. 波的相互反馈：
• 上层波通过其诱导的流场对下层波产生影响，反之亦然。
• 这种反馈可以增强两波的幅度（振幅增长）。
2. 传播方向调整：
• 波的传播速度会因相互作用调整，使两波逐渐趋于相同的相位速度，最终实现相位锁定 (Phase-Locking)。
3. 持续增长：
• 在相位锁定状态下，两个 CRWs 的相互作用可以实现持续的振幅增长，导致斜压不稳定性。
4.典型大气场景中的斜压不稳定性
在对流层中，斜压不稳定性通常发生在：
• 高层急流 (Jet Stream) 附近，存在强烈的 PV 梯度；
• 地表温度梯度 较大的区域，例如锋区。
在这些条件下：
• 上层的波动与高层 PV 梯度相关；
• 下层的波动由地表的边界温度梯度驱动。

3.5.2 PV building blocks

斜压增长是潜势涡度 (PV) 波与边界潜势温度波相互作用的结果。通过将 PV 波看作大气动力学的“构件”，我们可以深入理解这些波的相互作用机制。以下将通过构件的数学描述、动力学特性以及其在斜压不稳定性中的角色展开讨论。
1. PV 构件的定义
在一个大气层中，PV 波可以被视为构件，其特性包括：
• 某一高度 (z = h) 处存在 PV 波，其他地方的 PV 为零；
• 该 PV 波诱导了风场和浮力扰动。
类似地，地表潜势温度波（边界波）也可看作构件，其特性是：
• 波动存在于地表 (z = 0)，并通过其诱导风场与 PV 波相互作用。
这些构件通过 PV 反演算子的作用建立联系。
2. 孤立 PV 波的数学描述
孤立 PV 波的数学表达为：
$$q\prime =q_1\delta (z-h)e^{ikx-i\omega t},$$
其中：
• $\delta (z-h)$ 是 PV 波在高度 z = h 的分布；
• $q_1$ 是 PV 波的振幅。
由 PV 反演关系，流函数可以写为：
$$\psi \prime ={\psi }_1\left(A{e}^{-\mu z}+B{e}^{\mu z}\right)e^{ikx-i\omega t},$$
其中：
• $\mu$ = k；
• A 和 B 是待定系数。

为了使远离 z = h 的地方 PV 波为零，需要满足：
• z > h：B = 0，流函数在远离波时指数衰减；
• z < h：A = 0，流函数同样指数衰减。
最终，诱导流函数的形式为：
$$\psi \prime =\{\begin{array}{ll}{\psi }_1{e}^{-\mu (z-h)},& z>h,\\ {\psi }_1{e}^{\mu (z-h)},& z<h.\end{array}$$
3. 边界潜势温度波的动力学
对于地表的边界波，其浮力扰动可表示为：
$$b\prime =f_0\frac{\partial \psi \prime }{\partial z}.$$
结合流函数的表达，可以求得：
$$b\prime =N{\psi }_1\mu \left(-A{e}^{-\mu z}+B{e}^{\mu z}\right)e^{ikx-i\omega t}.$$
对于边界波 (z = 0)，为了使流函数满足边界条件（无无限增长），需令 B = 0。因此：
$${\psi }_1/b_1=-\frac{1}{N\mu A}.$$
4. PV 构件的物理意义
• “内核罗斯贝波” (Kernel Rossby Wave, KRW)：
孤立 PV 波在某一高度 z = h 处诱导的流场，被称为“内核罗斯贝波”，其流场是 PV 反演算子的格林函数 (Green Function)。
• 构件之间的相互作用：
PV 波的流场可以激发边界波，但由于下边界 PV 梯度为零，边界波无法反向影响 PV 波。这种相互作用是单向的。
5. 斜压不稳定性的实现条件
要实现斜压不稳定性，系统中必须存在：
1. 至少一个高度层具有非零 PV 梯度；
2. 地表或其他边界存在潜势温度波。
例如：
• 高层急流 (Jet Stream) 的 PV 梯度与地表温度梯度耦合；
• 这些构件之间的相互作用可导致持续的振幅增长，形成斜压不稳定性。
图示分析（图 22）

图 22 展示了不同情况下的流函数分布：
1. 孤立 PV 波远离边界 (22a)：
流函数在波的两侧对称衰减。
2. PV 波靠近边界 (22b)：
流函数在边界上方和下方的衰减不同。
3. 地表温度波 (22c)：
流函数仅在地表上方衰减。
4. PV 波和地表波的结合 (22d)：
显示了 PV 波和边界波的相互作用。