AP算法存在的固有缺陷是它不能对包含很多子类的category进行建模,而在image categorization, face categorization, 多字体optical character recognition,手写数字分类,每个category可能包含很多子类。
比如说,在自然场景类别可能包含很多主题,比如说,街景中可能包含一些主题,比如road,car,pedestrian,building等等。

在OCR和手写数字分类问题中,代表letter或digit的类可能由多个子类组成,每个子类代表着不同的style或者字体。显然,我们用一个代表点来统一表示这些子类是不合理的。
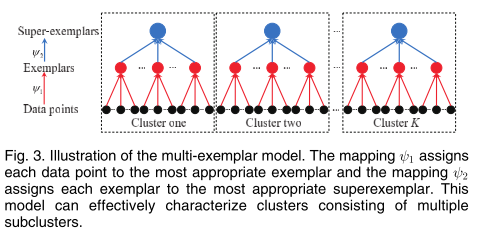
这篇论文提出了MEAP算法。每一个cluster都是自动决定exemplars和superexemplars的数目,每个数据点都自动分配给最接近的exemplar,而每个exemplar都分配给最接近的superexemplar。
superexemplar定义为代表一类cluster的所有exemplars中的最具代表性的那一个。
所以目标函数是 最大化数据点和代表点(exemplar)之间的相似度,以及exemplar和superexemplar之间的相似度。
直接求解这个问题是NP困难的。所以我们可以使用max-sum belief propagation,可以产生对初始化信息不敏感的算法。
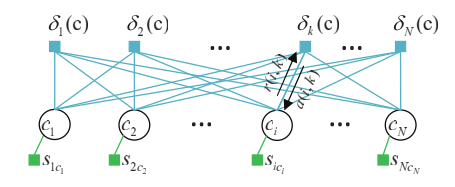
AP算法复习
在之前的博客中已经有过具体的介绍,为了数学符号表示的一致性,这里用新的数学表达式再表示一次。
给定一个用户定义的N个数据点的相似矩阵
[sij]N×N
,我们的目标是获得一个labels的valid configuration
c=[c1,c2,...,cN]
,来优化目标函数:
而 δk(c) 是一个exemplar-consistency约束,就是说如果有数据点i选择k作为代表点,也就是满足 ci=k ,那么k必须同时也是自己的代表点,也就是 ck=k
更新迭代的过程可以浓缩到下面几行:
最后的类别向量
c=[c1,...,cN]
的计算方法为:
MEAP
假设
[sij]N×N
是一个用户定义的相似度矩阵,
sij
代表着数据点i和代表点j之间的相似度,
[lij]N×N
代表着代表点i和潜在的super-exemplar j之间的相似度。
我们的目标是最大化所有数据点和它们对应的代表点之间的相似度
S1
,同时最大化代表点和superexemplar之间的相似度
S2
。
模型
假设C是assignment 矩阵,非对角线元素代表数据点j是数据点i的代表点
cij=1
,也就是
ψ1(i)=j
, 对角线元素代表
cii∈{1,...,N}
代表着
cii
是代表点i的superexemplar。
其中 [⋅] 是Iverson notation,当true时,取值为1。
我们可以得到
S1+S2=∑Ni=1∑Nj=1Sij(cij)
。同时必须满足下面3个约束:
1) 每个数据点i必须只能分配给一个代表点
2) 代表点一致性约束
如果数据点i选择了数据点j作为代表点,那么数据点j本身必须是代表点。
3) superexemplar一致性约束
如果数据点i选择了数据点k作为superexemplar, 那么k必须同时选择自己作为superexemplar。
所以MEAP的目标是最大化下面的目标函数:
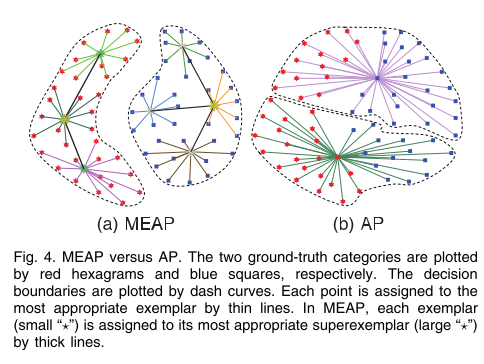
上图描述的是一个多层的结构,S1评估的是within-subcluster 的compactness,高层的
ψ2
描述的是exemplar 和superexemplar之间的关系。
根据single-exemplar的理论,最大化within-cluster 相似度会自动最大化between-cluster separation.
从最大化margin clustering的角度,MEAP比AP要好,见下图:
优化
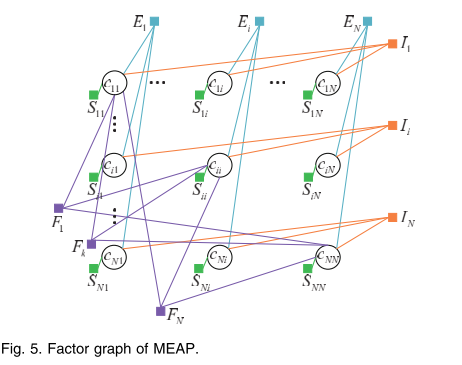
MEAP的因子图如下图:
多代表点的模型是单代表点的模型的普及,对其进行优化是NP-hard的。因此,我们使用max-sum belief propagation,这是一个local-message-passing 算法,它会收敛到局部最大值。
(可以发现对角线的变量多连接了F的函数),也就是 superexemplar的一致性约束。
上图中圆形表示的变量节点,方形表示的是函数节点。
从变量到函数,将与这个变量连接的函数的信息求和(除了接收信息的函数以外)。
从函数到变量,包括除该变量外所有函数变量的maximization。
其中
X=ne(f)
是函数
f
的参数集。(或者我们可以理解成与该函数节点连接的所有变量节点)
这里我们可以发现对角线和非对角线的变量节点很不同,所以我们对它们分开进行讨论。
非对角线元素的Messages
左图有5种messages,与
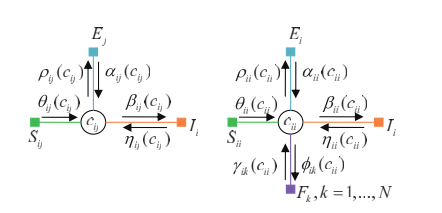
非对角线元素
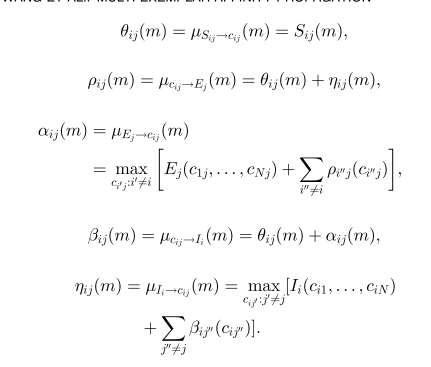
对角线元素
求解过程
非对角线变量
对于非对角线结点,
m=cij
我们来讨论
cjj
,将这一项单独写出来,它的取值可以是1也可以是0
第一种情况:
如果是1,也就是m=1, 如果数据点i选择j作为代表点,那么j必须是一个代表点,这时
Ej(c1j,...,cij)
为0,而别的数据点
i′
可以选择j作为代表点也可以不选,也就是
ci′j
的值不定。
第二种情况:
m=0,也就是说i没有选j作为代表点,我们再讨论数据点j的情况,如果数据点j本身是一个代表点,别的数据点
i′
要么选它作为数据点,要么不选,就如第一种情况的结论,但是如果j本身不选自己,那么逆否命题成立我们可以推知,一定有
cjj=0=>ci′j=0
, 所以可以得到
∑i′:i′≠iρi′j(0)
对于
ηij
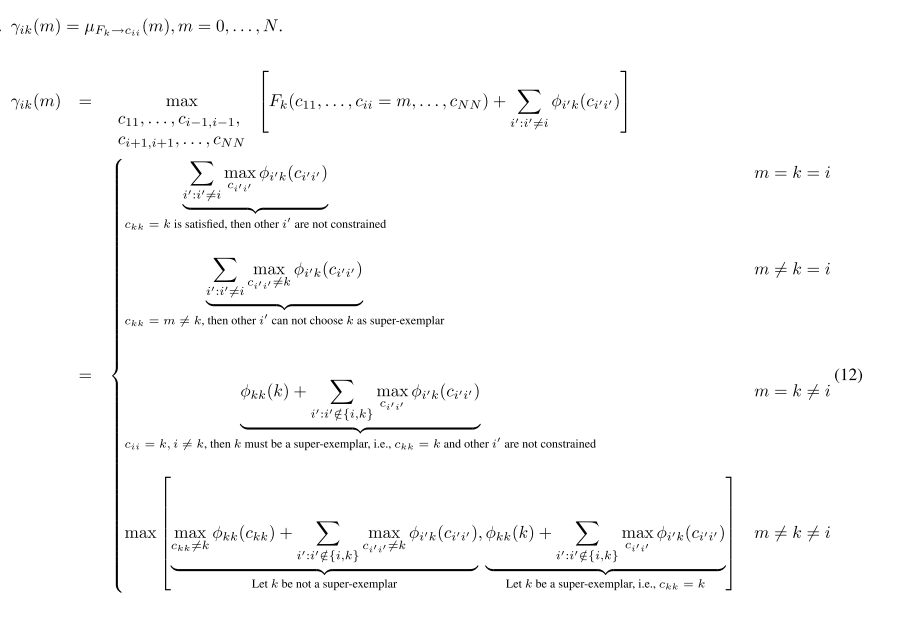
,同样是从函数结点到变量结点。
第一种情况,
cij=1
, 由于唯一性约束,也就是它只能有一个代表点,那么
β
参数
cij′
必须是0。
第二种情况,如果是0,那么假设它的代表点是
j′
,再讨论这个
j′
是不是i本身,除去
j′
的代表点的所属权都必须是0。
(我一开始有点疑惑,因为大前提已经是
i≠j
,后来我反应过来这只是对
cij
的讨论,而公式中覆盖的条件是全面的。)
对角线变量
对于对角线上的变量,如果它们本身是代表点,那么它们的取值为
{1,...,N}
, 如果它们不是代表点,那么取值为0。
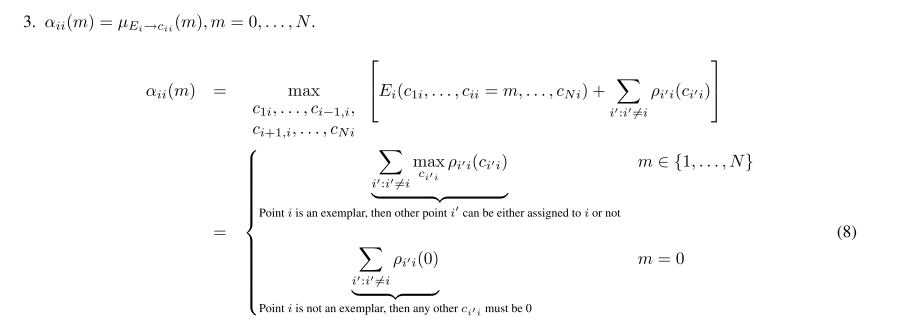
(1)
如果i是代表点,也就是
cii=m,m∈{1,...,N}
那么别的数据点
i′
可以选择它或者不选它。
此时
Ei(c1i,...,cii=m,...,cNi)=0
(2)
如果i本身不是代表点,那么
ci′i=0

(1)
如果i本身是一个代表点,也就是它选自己当代表点,所以它不能再选别人当代表点,由唯一性约束,那么别的
cii′=0
(2)
如果i不是代表点,假如它选了i’,那么它不能选别的数据点作为代表点,所以可得
对于
γ
的讨论比较复杂,
(1) 如果
cii=k=i
,也就是说一个代表点k,选了自己作为自己的superexemplar.
(2) 如果
cii≠k=i
可以推出
ckk≠k
, 也就是说数据点k并没有选自己作为superexemplar,那么别的数据点
i′
也不能选自己k作为superexemplar。
(3)
cii=k≠i
如果i为代表点,选择k作为超级代表点(superexemplar),同时
k≠i
,那么k本身必须也是一个代表点同时选择自己作为超级代表点,也就是
ckk=k
,而别的除了i和k的数据点并没有限制。
(4)
cii≠k≠i
i没有选择k作为超级代表点,我们可以对k的情况进行讨论,如果它本身不是超级代表点,也就是
ckk≠k
,
这一项单独写出来可以得到
如果k本身是超级代表点,
ckk=k
,单独写出来是:
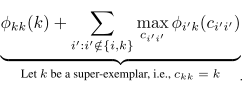
最后的结果是两项的较大值。
Message summary与代码解读

S: similiarty matrix,n*n的矩阵
L: linkage matrix, n*n的矩阵
Rhoij :
ρ~ij
Rhoim:
ρ~mi
Alphaij:
α~ij
(N*N) Alphai:
α~ii
(N*1)
Betaij :
β~ij
Betaim :
β~mi
Etaij:
η~ij
(N*N) Etaii :
η~ii
(N*1)
Gammaik:
γ~ik
Phiik :
ϕ~ik
Rhoij=zeros(N,N); Rhoim=zeros(N,N);
Alphaij=zeros(N,N); Alphai=zeros(N,1);
Betaij=zeros(N,N); Betaim=zeros(N,N);
Etaij=zeros(N,N); Etai=zeros(N,1);
Gammaik=zeros(N,N); Phiik=zeros(N,N);更新 ρ
%% rho
OldRhoij=Rhoij;
Rhoij=S+Etaij;
Rhoij=(1-lambda)*Rhoij+lambda*OldRhoij; %rho_ij
OldRhoim=Rhoim;
Rhoim=repmat(diag(S)+Etai,[1,N])+L+Gammaik;
Rhoim=(1-lambda)*Rhoim+lambda*OldRhoim;更新 α
OldAlphaij=Alphaij;
OldAlphai=Alphai;
Rp=max(Rhoij,0);
for k=1:N, Rp(k,k)=max(Rhoim(k,:)); end;
A=repmat(sum(Rp,1),[N,1])-Rp;
dA=diag(A); Alphaij=min(A,0);
for k=1:N, Alphai(k)=dA(k); end;
Alphaij=(1-lambda)*Alphaij+lambda*OldAlphaij;Alphai=(1-lambda)*Alphai+lambda*OldAlphai;更新 β
Betaij=S+Alphaij;
Betaim=repmat(diag(S)+Alphai,[1,N])+L+Gammaik;更新 η
B=Betaij; [Y,I]=max(B,[],2);
for i=1:N, B(i,I(i))=-inf; end;%最大值赋值为负无穷
[Y2,I2]=max(B,[],2);% Y2代表次大值
R=repmat(Y,[1,N]);
当j的位置刚好对应最大值时,由于
j′≠j
所以取次大值
这一步得到
for i=1:N,
R(i,I(i))=Y2(i);
R(i,i)=-inf;
end;接下来计算:
T=zeros(N,N);
for i=1:N, T(i,:)=max(Betaim(i,:)); end;
接下来计算:
Etaij=-max(R,T);接下来计算
T=Betaij;
for i=1:N, T(i,i)=-inf; end;%除去i'不等于i的情况
Etai=-max(T,[],2);更新
γ
这一步计算
OldGammaik=Gammaik;
RPhiik=max(Phiik,0);
for k=1:N, RPhiik(k,k)=Phiik(k,k); end;
Gammaik=repmat(sum(RPhiik,1),[N,1])-RPhiik;
对于对角线元素,通过上面的计算已经求出,也就是Gammaik的对角线,所不同的是对非对角线,还有一个min函数的截断。所以先存储对角线元素,随后对矩阵进行min函数的截断,再单独赋值。
dGammaik=diag(Gammaik); Gammaik=min(Gammaik,0);
for k=1:N, Gammaik(k,k)=dGammaik(k); end;
Gammaik=(1-lambda)*Gammaik+lambda*OldGammaik;更新
ϕ
计算
OldPhiik=Phiik;
LG=L+Gammaik; [Y,I]=max(LG,[],2);
for i=1:N, LG(i,I(i))=-inf; end; [Y2,I2]=max(LG,[],2);
R=repmat(Y,[1,N]);
for i=1:N, R(i,I(i))=Y2(i); end;计算 sii+α~ii+η~ii
SAE=repmat(diag(S)+Alphai+Etai,[1,N]);
Phiik=L-max(R,-SAE);
Phiik=(1-lambda)*Phiik+lambda*OldPhiik;Assignment matrix
计算
cij
的所有输入信息的和,随后求解使得
c^ij
最大的值。
C=zeros(N,N);
C(Alphaij+Rhoij>=0)=1;%非对角线
[a,b]=max(Rhoim,[],2);
for i=1:N, if a(i)+Alphai(i)>=0, C(i,i)=b(i); else C(i,i)=0; end; end;%对角线
if isequal(OldC,C), stayiter=stayiter+1; else stayiter=1; OldC=C; end;
if stayiter>convits
% further check for validation
exemplar_idx=zeros(N,1);
validflag=1;
for i=1:N
a=find(C(i,:)~=0);
if length(a)~=1, validflag=0; break; else exemplar_idx(i)=a(1); end; % points to exemplars
end
if validflag==1
a=find(diag(C)~=0);
if length(a)<=1%只有一个代表点
validflag=0;
else
superexemplar_idx=zeros(length(a),2);
superexemplar_idx(:,1)=a;
superexemplar_idx(:,2)=diag(C(a,a));
sa=unique(superexemplar_idx(:,2));
if ~isequal(diag(C(sa,sa)),sa), validflag=0; end; % exemplars to super-exemplars
end
end
if validflag==0 % invalid results! continue iterating!
stayiter=1; OldC=zeros(N,N);
else
disp(['iteration number ' num2str(iter)]);
break;
end
end
end计算net similarity
T=diag(L);
netSim=sum(S(C~=0))+sum(T(diag(C)~=0));








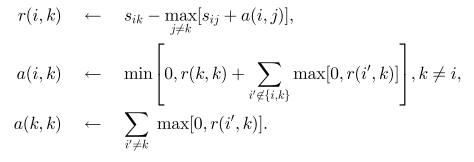
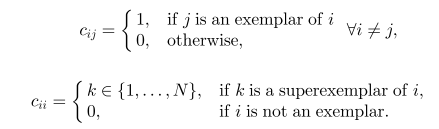
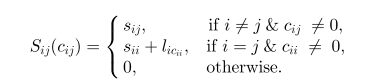
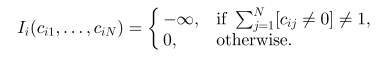
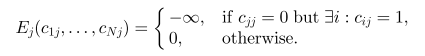
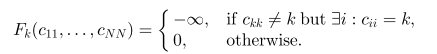
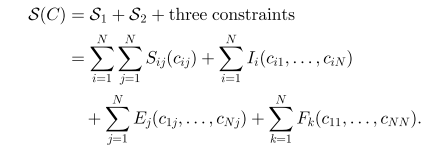
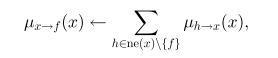
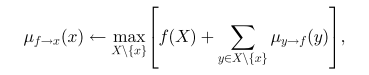
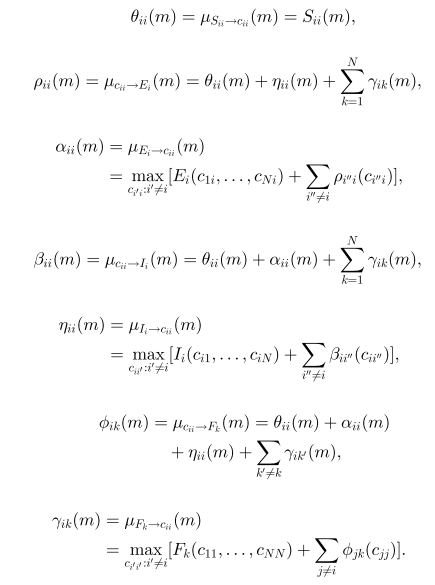
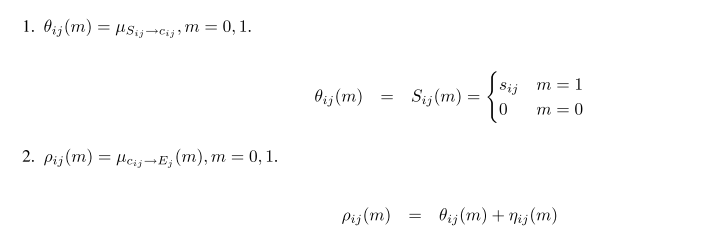

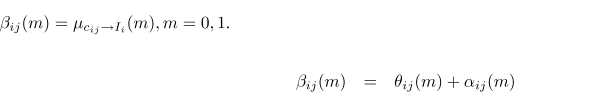
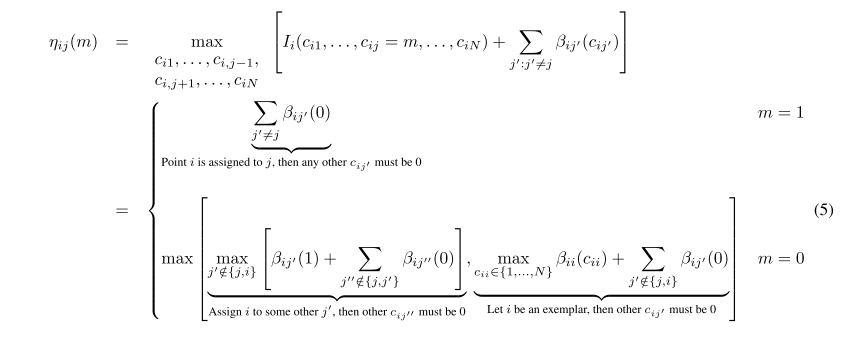
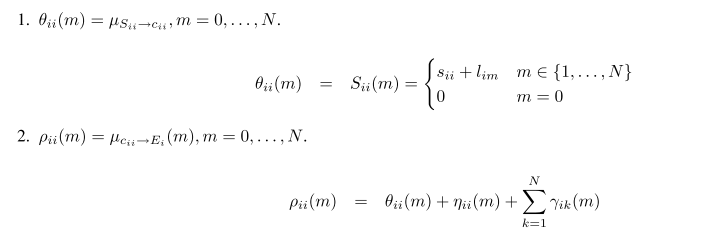
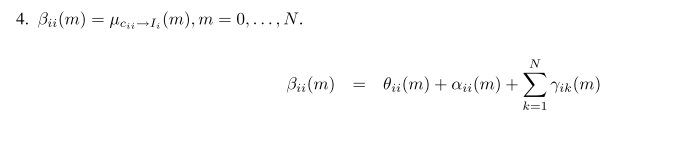
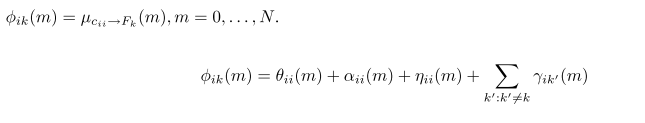

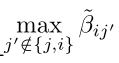
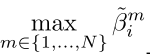
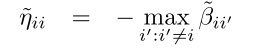
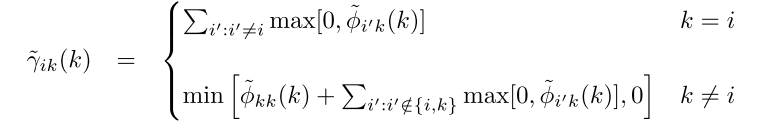
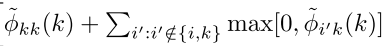
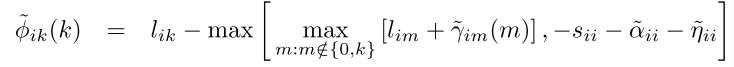
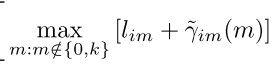
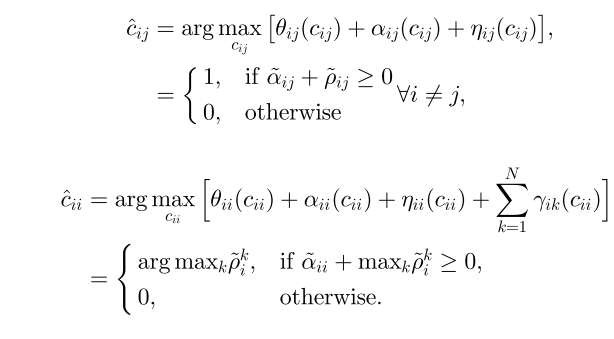
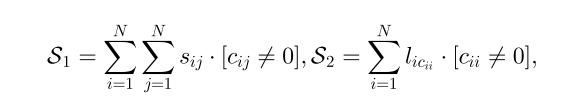














 3129
3129

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








