机器学习笔记06-吴恩达机器学习课后习题(1)

前言

本节主要分析吴恩达教授授课过程中的课后练习题计算过程，通过习题进一步复习巩固前边所学知识。

1、课后习题：ex1
下载地址：https://pan.baidu.com/s/158L1eMLSlkWUYvHe_9iVQw
提取码：xodk
2、使用工具：Octave 6.1.0，官网：https://wiki.octave.org/GNU_Octave_Wiki
该版本下载地址：https://www.gnu.org/software/octave/download

习题简述

ex1习题主要包含3部分内容的练习，单变量线性回归、多变量线性回归以及正规方程的基本使用流程。首先对ex1文件夹下的文件有个基本的认识和了解：图中未标记的文件主要用于代码提交，可以不关注。

训练的目的主要有两点：
（1）熟练掌握所学算法的具体流程，并能通过代码的方式实现；
（2）掌握Octave基本语法，能通过Octave的方式进行代码实现。此处默认大家都对Octave有了基本的了解，Octave类似与Matlab。

m文件在Octave/Matlab中分为两种，函数文件或者脚本文件。
一种为脚本文件，就是由一堆命令构成的，里面第一行不是 function 开头，这种文件比如是myfun.m 就在命令窗口里输入myfun回车就行，matlab会把m文件中的命令都运行一次。
另一种为函数文件，第一行为function ，比如说 function y=myfun(x)，这种文件函数名与文件名必须是一致的，在命令窗口里输入myfun(x), x是运行参数，回车即运行。

热身训练：输出一个5*5的单位矩阵。
方法一：直接输出；

eye(5)

方法二：通过函数文件实现；

pwd           %显示当前所在路径
cd 'G:\Desktop\machinelearning\Ngex1\ex1'   %进入项目路径
%addpath('G:\Desktop\machinelearning\Ngex1\ex1') %也可通过添加路径的方式
warmUpExercise

单变量线性回归

问题背景：假如你是餐馆老板，已知若干城市中人口和利润的数据（ex1data1.txt），用线性回归方法计算该去哪个城市发展。

综述

直接运行脚本文件ex1.m，即可得到整个单变量线性回归的结果。方法很简单，只需要在Octave命令行中键入ex1即可。

pwd      %查看当前路径，保证路径正确，或者在此之前已经添加过项目路径。
ex1      %执行ex1.m脚本

接下来只需要按照提示敲回车即可看到最终预测结果。

分解步骤

至于脚本和函数的实现方式，不再细讲，代码中有很清晰的注释，大家可以自行查看。接下来咱们不调用脚本，通过Octave自行实现本题，其实就是脚本流程的复现过程。

1、首先回顾一下单变量线性回归的流程
①根据数据选取合适的模型，此处选用单变量线性回归模型，即

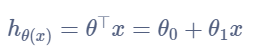
②代价函数计算： 如何通过代码实现计算代价函数。

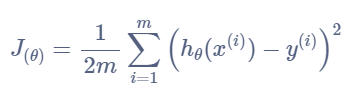
③梯度计算：如何通过代码计算梯度，实现$\theta$的同步更新。
参数更新方式：

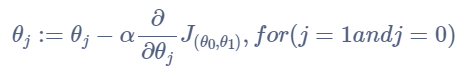
求导结果：$x_0=1$，因为${\theta }_0$的系数为1，其实就相当于$x_0$恒为1。推导过程之前总结过。

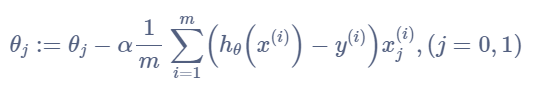
2、基本知识点回顾完毕，接下来开始构思怎么得到该模型的最优参数，也就是得到最终的预测函数。首先明确我们的目标，求出最优的参数${\theta }_0和{\theta }_1$。
然后，考虑该怎么求解？其实就是通过代价函数一步一步迭代，当代价函数值最小时，即得到最优参数。最后，怎么迭代？$\theta$值的组合有很多种，需要有一种算法来帮助我们迭代。梯度下降算法就是帮助我们进行迭代更新参数的。

代码实现

step1：首先加载数据，观察数据分布情况。

%加载数据前，请先保证当前路径
pwd         %查看路径
data = load('ex1data1.txt');     %加分号不会显示详细结果，不加分号会显示结果
data             %查看加载的数据，第一列表示城市人口，第二列表示利润
x = data(:,1);   %x为第一列所有数据，冒号表示取行的所有，1表示第1列
y = data(:,2);   %y为第二列所有数据
plot(x,y,'xr');  %显示关于x，y的图像，xr表示以‘x’的方式红色输出
xlabel('Population of City in 10,000s');  %x轴标签
ylabel('Profit in $10,000s');    %y轴标签

step2：观察图像，我们选择单变量线性回归模型来预测。首先熟悉一下代价函数的计算。当我们有两个值${\theta }_0和{\theta }_1$的时候，如何计算此时的代价函数，根据公式：$J_{\left(\theta \right)}=\frac{1}{2m}{\sum }_{i=1}^m{\left(h_{\theta }(x^{(i)})-y^{(i)}\right)}^2$。

计算过程：假设只取前3（m = 3）行数据进行代价函数的计算，计算方式如下表所示。首先我们需要一个初始${\theta }_0和{\theta }_1$的值，此处设定初始值为${\theta }_0=2，{\theta }_1=3$，此时计算的代价函数结果为$J=48.32$。

Octave的实现需要借助矩阵相关知识。因为使用矩阵不仅可以简化代码，而且可以提高运算效率。当然这个流程你也可以使用类似$for$循环的方式实现，但是不建议这么做。

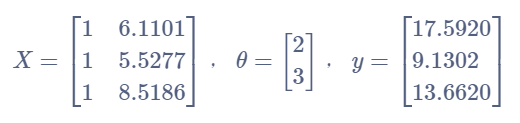
至此，每个矩阵都已经构建完毕，$X$第一列为什么都是1，熟悉矩阵操作的朋友都明白，因为它永远和$\theta$矩阵中的第一行相乘，即公式中的${\theta }_0$。

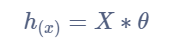
所以代价函数可以用矩阵的形式表示为：
$$J_{(\theta )}=\frac{1}{2m}\sum _{i=1}^m{\left(X\ast \theta -y\right)}^2$$

%该部分代码是在之前代码的基础上，此时已经得到了x和y的对应数据
%首先构建矩阵x，因为之前得到的矩阵x只有1列，需要在其左边再加1列1
m = length(y); %首先获取有多少行数据
x = [ones(m,1) x];  %在x之前加一列1，也可写成[ones(m,1) data(:,1)]。
%y = data(:,2);   %在此之前已经获得，可省略
theta = [2;3]  %设定theta的值，该矩阵为2行1列
J = 0;
J = sum((x * theta - y).^2) / (2 * m);   %代价函数表示

step3：运用梯度下降算法计算最优参数。注意：参数需要同步更新。$${\theta }_j:={\theta }_j-\alpha \frac{1}{m}\sum _{i=1}^m\left(h_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)x_j^{(i)},(j=0,1)$$前边已经说过，用矩阵表示$h_{(x)}=x\ast theta$，还是取前3行数据进行说明：
重点说明一下后边的$x_j^{(i)}$，此处的乘为点乘，即对应位相乘，当$j=0$时，即求取${\theta }_0$的值，那么此时$x_0^{(i)}$就表示取矩阵$x$中的第0列所有数据。

因为在Octave中矩阵下标都是从1开始的，所以第0列其实就是第1列，第1列就是第2列。所以公式和实际的代码还是有点区别的。

%在此之前保证已经构建好x和y矩阵
%定义初始alpha、迭代次数、theta值
alpha = 0.01；  %表示步长、学习率
iterations = 1500；  %表示迭代循环1500次
theta = zeros(2,1);  %theta0和theta1均为0
%下边开始进行迭代
J_history = zeros(iterations ,1); %将代价函数结果为矩阵，可以看出为1500行1列
theta_s = theta;    %拷贝theta初始值
 
for iter = 1 : iterations
    theta(1) = theta(1) - alpha / m * sum((x * theta_s - y).*x(:,1));
    theta(2) = theta(2) - alpha / m * sum((x * theta_s - y).*(x:,2));
    theta_s = theta;
 
    J_history(iter) = sum((x * theta - y).^2) / (2 * m); %代价函数结果
end

至此，1500次迭代已经结束，损失函数值从32.072将为4.4834。最终预测的${\theta }_0=-3.6298，{\theta }_1=1.1663$。

step4：画出预测结果图像。三维图像参考ex1.m文件，此处省略。

hold on;
plot(x(:,2),x*theta,'-');  %以划线的方式画出预测模型

多变量线性回归

问题背景：买房子，已知一系列数据，根据房屋大小和卧室数量两个特征，预测房子价格，数据在(ex1data2.txt)中。

说明：单变量线性回归其实是多变量线性回归的一种特殊情况，大体思路其实是一样的。主要在于梯度下降算法，因为单变量线性回归只有两个$\theta$值，所以在循环中可以写成${\theta }_1=....;{\theta }_2=....;$。当随着特征增多时，假设有100个特征，那么此时我们就有101个$\theta$值，再像这样列举就会很繁琐。所以我们得找到一个通用的表示方法来简化此步骤。

假设$x$为3*3矩阵，$\theta$为3 * 1矩阵，$y$为3 * 1矩阵。那么式中$(x\ast theta-y)$为3 * 1矩阵。此时要给每一项都要乘以对应列的$x$。我们将$x$进行转置。那么$x$就变为：

此时用$x^{\top }\ast (x\ast \theta -y)$，即就是求和所得结果。所以最终梯度下降算法可表示为，注意此处的$\theta$为矩阵，而不再是单独的值：
$$\theta :=\theta -\alpha \frac{1}{m}{X}^{\top }(x\theta -y)$$

注意：查看数据我们可以发现，特征值的范围相差很大，房屋大小基本都在1000以上，而卧室基本都在10以内。此时为了更快的拟合数据，我们需要进行特征缩放。
特征缩放的目的是保证每个特征基本都在-1 < $x$ < 1之间，当然，接近这个范围就可以，没必要必须在这个范围之间。

$$z=\frac{x-\mu }{\sigma }$$

其中$x$表示当前特征值，$\mu$表示该平均数（房屋大小的平均值），$\sigma$表示标准偏差（也可以用房屋大小中最大值-最小值）。

data = load('ex1data2.txt');  %加载数据
y = data(:,3);     %y为数据第3列
m = length(y);     %得到样本数量
x = [ones(m,1) data(:,1:2)]; %得到x矩阵
%特征缩放
mu = mean(x);
sigma = std(x);
%x_norm = (x - mu) ./ sigma;  %这个写法其实不对，因为mu最终为3行1列，而x为47行3列，应使用下边的方法，将mu和sigma转换为47行3列。但是Octave也可正确计算该式。
x_norm = (x - repmat(mu,size(x,1),1)) ./ repmat(sigma,size(x,1),1);
 
%定义初始alpha、迭代次数、theta值
alpha = 0.01；  %表示步长、学习率
iterations = 8500；  %表示迭代循环8500次
theta = zeros(3,1);  %theta0和theta1和theta2均为0
%下边开始进行迭代
J_history = zeros(iterations ,1); %将代价函数结果为矩阵，可以看出为1500行1列
 
for iter = 1 : iterations
    theta = theta - alpha / m * x_norm ' * (x_norm * theta - y); %得到theta矩阵
 
    J_history(iter) = sum((x_norm * theta - y).^2) / (2 * m); %代价函数结果
end
%后期在预测过程中，给出的特征值都需要按照同样的特征缩放方式进行缩放。
%具体参考ex1_multi.m

正规方程

该方法适用于样本较少的情况，如果样本太多，那么正规方程就会特别慢。它不需要通过迭代计算最优参数，可直接得到最优$\theta$值，而且不需要进行特征缩放。

$$\theta ={\left(X^{T}X\right)}^{-1}{X}^{T}y$$

theta = pinv(x' * x) * x' * y;  %pinv表示逆运算，'表示转置运算。