Competition Among Parallel Contests（博弈论+机制设计） 论文阅读笔记

一、基本信息

• 题目：平行竞赛之间的竞争
• 作者：Xiaotie Deng, Ningyuan Li, Weian Li, and Qi Qi

二、文章摘要

• 以下内容取自原文摘要部分：
• 我们研究一个多个竞赛同时举行的模型，其中每个参赛者选择其中一个竞赛参与以及每个竞赛的设计者决定奖项结构从而竞争以吸引参赛者的参与。首先我们分析了参赛者的策略行为并且完全刻画了对称贝叶斯纳什均衡BNE。对于竞赛设计者的策略，当其他设计者的策略是已知的时候，我们表示计算最优响应是NP-Hard问题并且提出了一个输出$1-ϵ$近似最优响应的完全多项式时间的近似算法FPTAS。当其他设计者的策略未知时，我们给出了对于单个设计者策略的最坏情况分析。我们给出了任意策略效用函数的上界，并且提出了一个策略可以保证获得最坏情况下效用上界固定比例的效用。
• 关键词：
• 竞争、平行竞赛、均衡行为、最优响应、安全等级

三、背景

• 目前大部分竞赛理论的研究内容都关注于单一竞赛，并且已经有了较为成熟的研究成果。越来越多的竞赛被同步举行，平行竞赛的研究受到更少的关注。在本文的模型中，只允许参赛者挑选一个竞赛参加。每个设计者的目标是最大化参赛者的价值总和。每个参赛者想要最大化她所赢得的奖励。在本文的模型中有两个博弈，一个是参赛者决定参与哪个竞赛，另一个是设计者设计奖项结构去吸引参赛者。
• 文章结构：第二部分介绍模型以及一些重要定义。第三部分完整描绘参赛者的均衡行为。第四部分我们放松竞赛设计者的可行策略空间并提供一些技术结果。第五部分研究了单一竞赛设计者的最优响应并且设计了FPTAS算法以输出近似最优响应。第六部分我们关注于先行者策略的安全等级并且提出带有常数竞争力安全等级的策略架构。第七部分使用取整技术以在带有微小设计者效用损失的原始可行区域中的离散奖项结构。第八部分总结展望。

四、模型

• 共有$m$个竞赛$n$个参赛者，分别表示为 j ∈ [ m ] = { 1 , 2 , . . . , m } , i ∈ [ n ] = { 1 , 2 , . . . , n } j\in [m]=\{1,2,...,m\},i\in [n]=\{1,2,...,n\} j∈[m]={1,2,...,m},i∈[n]={1,2,...,n}。$j$既表示某个竞赛，也表示对应的竞赛设计者。竞赛设计者$j$的平均预算为$t_j$，所设计的奖项结构为$\overrightarrow{w_j}=(w_{j1},w_{j2},...,w_{jn}),{\sum }_{i=1}^n{w}_{ji}\le n{t}_j$。参赛者$i$有私有的能力$s_i$，独立同分布于公共已知的分布$G$，我们用分位点$q=1-G(s)$来表示能力，$q$越小表示比当前参赛者能力强的参赛者少，也就是排位更考前。
• 模型包含三个阶段：
  第一阶段GoD：所有设计者设计并公布自己的奖项结构给所有的参赛者。
  第二阶段GoC：参赛者$i$已知所有竞赛的奖项结构，选择竞赛的纯策略表示为$J_i\in [m]$，混合策略表示为$\overrightarrow{{\pi }_i}(q_i)=({\pi }_{i,1}(q_i),{\pi }_{i,2}(q_i),...,{\pi }_{i,m}(q_i))$。$\mathbb{S}$表示混合策略的策略空间。所有参赛者的纯策略为$\mathbf{J}=(J_1,J_2,...,J_n)$，混合策略为$\pi =(\overrightarrow{{\pi }_1}(q_1),\overrightarrow{{\pi }_2}(q_2),...,\overrightarrow{{\pi }_n}(q_n))$。
  第三阶段：每个竞赛的参赛者集合 I j = { i : J i = j } I_j=\{i:J_i=j\} Ij​={i:Ji​=j}，然后根据参赛者的分位点升序排列依次分配奖项。（rank-by-skill allocation）
• 在纯策略组合$\mathbf{J}$下参赛者$i$的效用函数为：
  $$u_i(\mathbf{J})=w_{J_i,rank(i,J_i)}$$
  其中 r a n k ( i , J i ) = ∣ { i ′ ≠ i : ( q i ′ ≤ q i ) ∧ ( J i ′ = J i ) ) } ∣ + 1 rank(i,J_i)=|\{i'\neq i:(q_i'\le q_i) \land (J_i'=J_i))\}|+1 rank(i,Ji​)=∣{i′=i:(qi′​≤qi​)∧(Ji′​=Ji​))}∣+1，表示他在当前竞赛中的排位。
• 在GoC中参赛者的博弈是不完全信息的（参赛者的能力是私有信息），因此我们主要考虑对称贝叶斯纳什均衡，也就是说所有参赛者共用一套相同的混合策略$\vec{\pi }(q)=({\pi }_1(q),{\pi }_2(q),...,{\pi }_n(q))\in \mathbb{S}$。纯策略的效用函数方便表达，混合策略的效用函数及其BNE需要定义Cumulative Behavior、Interim Allocation Function。
• Cummulative Behavior：所有参赛者采用相同的对称策略$\vec{\pi }(q)=({\pi }_1(q),{\pi }_2(q),...,{\pi }_n(q))\in \mathbb{S}$，对于每个竞赛$j$来说定义$H_{{\pi }_j}(q)$为如下：
  $$\begin{gathered} H_{{\pi }_j}(q):={\int }_0^q{\pi }_j(u)du \\ Pr[(q_i\le q)\wedge (J_i=j)]=H_{{\pi }_j(q)} \end{gathered}$$
  $H_{{\pi }_j}(q)$的含义是，在竞赛$j$中出现参赛者打败$q$的概率。可以观察到，参赛者$i$在竞赛$j$中获得的奖项完全依赖于排名比他考前的参赛者数量，因此参赛者$i$在竞赛$j$中的期望效用可以表示为如下：
  $${\mathrm{E}}_{q_{-i}}\left[u_i\mid q_i=q,J_i=j\right]=\sum _{k=1}^n{w}_{j,k}\left(\begin{array}{c}n-1\\ k-1\end{array}\right)H_{{\pi }_j}(q{)}^{k-1}{\left(1-H_{{\pi }_j}(q)\right)}^{n-k}$$
  上式既是赛者$i$在竞赛$j$中的期望效用，也是竞赛$j$的设计者需要针对分位值为$q$的参赛者分配的奖项，这个数值只由$H_{{\pi }_j}(q)$决定。
• Interim Allocation Function：用函数$x_j(h)$来表示竞赛$j$的奖项结构
  $$\begin{gathered} h=H_{{\pi }_j}(q) \\ {\mathrm{E}}_{q_{-i}}\left[u_i\mid q_i=q,J_i=j\right]=x_j(h) \end{gathered}$$
• Symmetric Bayesian Nash Equilibrium：BNE策略${\vec{\pi }}^{\ast }(q)=({\vec{\pi }}_1^{\ast }(q),{\vec{\pi }}_2^{\ast }(q),...,{\vec{\pi }}_m^{\ast }(q))\in \mathbb{S}$，满足如下条件对于任意参赛者$i\in [n]$以及任意$q\in [0,1]$满足：
  $$\left\{j\in [m]:{\pi }_j^{\ast }(q)>0\right\}\subseteq \arg \underset{j\in [m]}{\max }{\mathrm{E}}_{q_{-i}}\left[u_i\mid q_i=q,J_i=j\right]=\arg \underset{j\in [m]}{\max }{x}_j(H_{{\pi }_j^{\ast }}(q))$$
• 我们假设参赛者的能力或者说$q$根据函数$v_j(q)$映射成对于设计者的收益，那么纯策略下以及混合策略下，竞赛设计者的效用函数如下所示。
  $$\begin{gathered} R_j(\mathbf{J})=\sum _{i\in I_j}{v}_j(q_i) \\ {R}_j(\vec{\pi })={\mathrm{E}}_{q_1,\cdots ,q_n}\left[\sum _{i=1}^n{v}_j\left(q_i\right){\pi }_j\left(q_i\right)\right]=n{\mathrm{E}}_{q\sim U[0,1]}\left[v_j(q){\pi }_j(q)\right]=n{\int }_0^1{v}_j(q)d{H}_j(q) \end{gathered}$$

五、结论

5.1 参赛者的均衡行为

• 传统博弈论的方法论是计算期望收益函数的FOC，但本文基于特殊设定提出一种新方法关注于累积行为。在完全信息设定下均衡特别容易分析，本文的方法可看作将不完全信息设定连续正则化为完全信息设定来分析。对于每个参赛者来说，比自己弱的参赛者不会对自己的收益产生影响，因此只需要关注比自己强的参赛者，这也是$q$与$H_{{\pi }_j}(q)$的设计思路（$q$是指在分布中比自己强的所占比例，$H_{{\pi }_j}(q)$是指在竞赛$j$中产生参赛者比自己强的概率）。混合策略$\vec{\pi }(q)$与累积行为$\vec{H}(q)$都可用来表征某个策略，但混合策略空间$\mathbb{S}$与累积行为空间$\mathbb{H}$是多对一的满射关系，也就是说$\mathbb{H}$中每一个元素都可以被$\mathbb{S}$中多个元素射到。因此用累积行为来表征策略更具唯一性，比混合策略更合适。因此我们就不考虑混合策略的BNE，而是考虑累积行为的CEB。下面是CEB的定义定理。
  

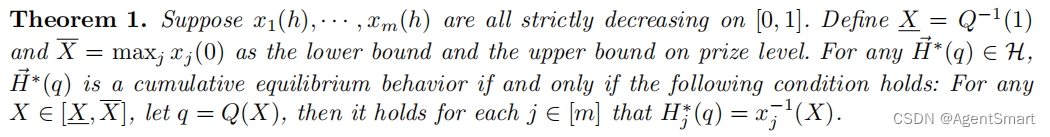
5.2 放松化以及简化

• 在本章节中，我们针对竞赛的可能分配规则进行放松化。真实竞赛中使用rank-by-skill的分配方式，任意rank-by-skill的分配方式都可以被某个临时分配函数来代表，放松化后称之为generalized model，在盖模型上定义参赛者的generalized对称均衡。这种放松化与正则化为设计者策略的分析带来了很大便利。
• Relaxation:interim allocation function $x_j(h)$用来代表竞赛的分配规则，其实就是竞赛该对何种竞争力的参赛者赋予多少价值的奖励。在generalized model中只需要iaf在$[0,1]$区间内非负且非增即可，预算限制条件${\int }_0^1{x}_j(h)dh\le t_j$。
• 上面的定理1实际是不完全版本，定理1要求iaf严格递减，从而要求所有竞赛的内部奖项必须严格递减，从而使得iaf必须连续。而实际上，iaf只需要满足非增且可能存在不连续的点。CEB定理的完整版本请见下面定理2。
  
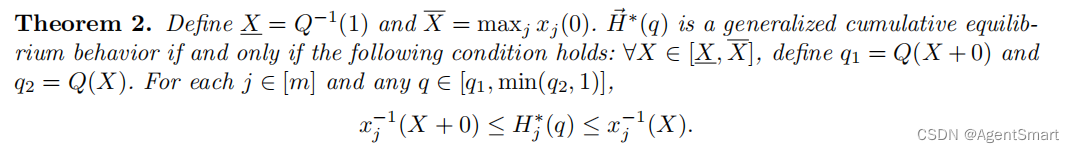
• Simplification:对于某个特定竞赛设计者的角度来说，竞赛的个数$m$可以简化为2个，通过将其他设计者看作一束并且联合他们的iaf。对于所有其他设计者$j^{\prime }\ne j$，预算为$t_{j^{\prime }}$，策略iaf为$x_{j^{\prime }}(h)$，捆绑成一束定义为：
  t − j = ∑ j ′ ≠ j t j ′ x − j ( h ) = m a x { x : ∑ j ′ ≠ j x j ′ − 1 ( x ) ≥ h } t_{-j}=\sum_{j'\neq j}t_{j'}\\ x_{-j}(h)=max\{x:\sum_{j'\neq j}x_{j'}^{-1}(x)\ge h\} t−j​=j′=j∑​tj′​x−j​(h)=max{x:j′=j∑​xj′−1​(x)≥h}
  并且预算$t_{-j}$对于$x_{-j}(h)$是合适的。并且通过Proposition 2得到，将其他所有设计者捆绑为一个，整个GoD简化为两个设计者的博弈，这种简化在设计者角度并不会影响参赛者的行为。因此这种简化在除特殊情况以外，都是合理可用的。
• GCEB的不唯一性：在$H^{\ast }(x_j(h),x_{-j}(h))$中可能存在多个GCEB，也就是说$x_j(h),x_{-j}(h)$可能在某个区间相等，换句话说设计者安排的奖项可能在不同均衡中吸引到不同水平的参赛者。定义某个设计者的最差效用与最优效用如下：
  $$\begin{gathered} R^{\text{Worst }}\left(x_j(h)\mid x_{-j}(h),v_j(q)\right)=\underset{H_j\in {\mathcal{H}}_j^{\ast }\left(x_j(h),x_{-j}(h)\right)}{\min }{\int }_0^1{v}_j(q)d{H}_j(q) \\ {R}^{\text{Best }}\left(x_j(h)\mid x_{-j}(h),v_j(q)\right)=\underset{H_j\in {\mathcal{H}}_j^{\ast }\left(x_j(h),x_{-j}(h)\right)}{\max }{\int }_0^1{v}_j(q)d{H}_j(q) \end{gathered}$$
  由累积行为函数定义最差效用与最优效用如下：
  
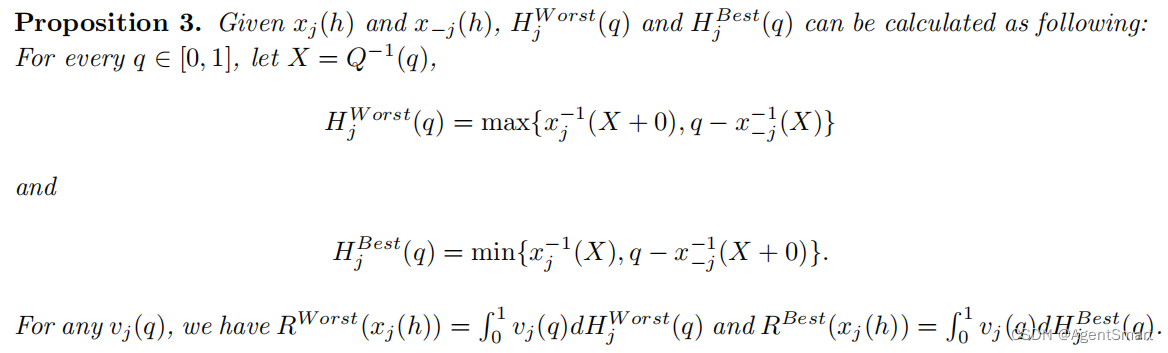
• Horizontal Stretching：水平伸缩帮助设计者建立占优策略。水平伸缩允许设计者从对手那里偷取策略，或者利用一些超出他预算范围内的策略。需要做的时调整iaf从而适应于其预算。为了降低开销，相较于降低奖项价值，降低奖项数目是更好的选择。设计到两个定义：C-占优与C-严格占优。如果我们以一个常数$C\in [0,1]$水平伸缩一个策略的话，可以保证获得一个比例效用，具体结论由Proposition 4、5给出。
  

5.3 设计者的最优响应（Last-mover Strategy）

• 本章节关注于Last-mover Strategy，也就是说某个设计者再观察到所有其他设计者的策略之后再做出策略最大化个人收益。首先明确最优响应问题的定义，然后证明了寻找最优last-mover策略是NPH问题，最后提出了FPTAS输出$(1-ϵ)$近似的最优响应。
• 为了定义最优响应问题，我们需要明确到底是在哪个均衡之下最优化设计者的效用。定理3发现无论我们选取哪个均衡，$R^{best},R^{worst}$的上确界都是相同的，也就是说最优响应的效用都是相同的，因此我们只需要求解$R^{best}$即可。
• 定理4表面求解最优响应的问题是一个NPH问题，因此考虑设计一个求解近似最优响应的算法。定义6定义了$ϵ$最优响应。定理5表明满足一定条件下，总有FPTAS算法可以求解$ϵ$最优响应（归约为knapsack problems）。

5.4 设计者的安全等级（First-mover Strategy）

• 本章节考虑First-mover Strategy，也就是说某个设计者在不知道其他设计者任何策略信息的前提下做出最优决策。考虑到针对其他设计者策略的不确定性，引入安全等级的概念来描述first-mover strategy的性能。

• 定义7定义了安全等级，安全等级代表了单一策略的最差性能表现，换句话说提供了单一策略能够实现效用的下界。通过假设对手根据horizontal stretching method设计策略可以得到安全等级对于任意iaf的上界，具体内容由Proposition 6呈现。
  
  

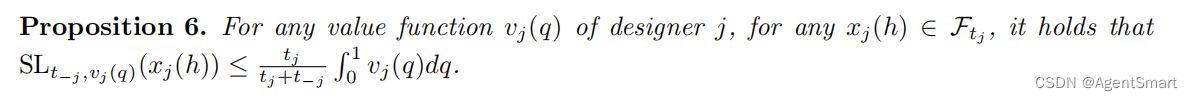
• 定义某个iaf是C-competitive的。定理6表示，对于任意估值函数$v_j(q)$以及任意预算$t_j,t_{-j}$，我们都可以建构一个分段连续的函数$x_j(h)$从而具有16-competitive的安全等级。
  

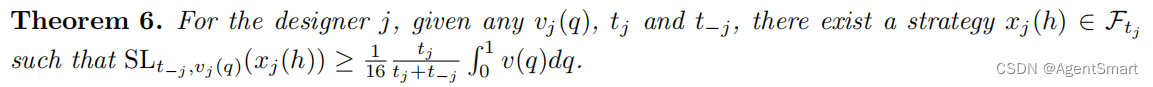
5.5 Rounding the Interim Allocation Functions

• 使用虚拟分配函数iaf的generalized model已经分析的比较彻底了，在该设定下设计者设计奖项结构不需要考虑参赛者人数$n$，但实际模型中参赛者人数$n$是个很重要的参数。我们表明，当$n$足够大时，任意iaf都可以被近似表示为一个rank-by-skill的分配方式。
  
• 当参赛者人数$n$足够大时，设计者可以首先找到一个合适的策略$x_j(h)$，然后根据定理7得到一个rank-by-skill的奖项结构，伴随着不显著的效用损失。但当$n$不足够大时，generalized model与original model通过定理7得到的策略所得的收益差距就比较显著了。

六、总结

• 总结来说，本文研究了多个竞赛设计者之间的竞争。一共有$n$个参赛者，每人都选择其中之一个竞赛参与，并且尽力最大化自己的期望奖项。设计者设计他们的奖项结构从而最大化参赛者的总价值。对于参赛者的博弈来说，我们针对于对称贝叶斯均衡SBNE给出了完整的描述。对于设计者的博弈来说，我们研究了在放松过的空间中最后行动者与最先行动者的策略设计。我们针对于最优响应问题提出了FPTAS，以及提出了带有16-competitive安全等级的最先行动者策略的建构。最后，我们将一个策略近似地还原为一个可执行的奖金结构。
• 我们提出了三个值得进一步讨论的未来研究工作方向。第一个方向是，我们只展示了相较于上界带有16-competitive安全性的最先行动者策略存在，但并不清楚是否存在更高安全性的策略。第二个方向是研究设计者的均衡并且描绘均衡奖项策略。最后一个方向是考虑参赛者可以不止参与一个竞赛的模型并且参赛者可以将自己的努力分配到多个竞赛上。