逻辑回归的代价函数通常使用交叉熵损失来定义。这种损失函数非常适合于二元分类问题。
本篇来推导一下逻辑回归的代价函数。
首先,我们在之前了解了逻辑回归的定义:逻辑回归模型是一种用于二元分类的模型,其预测值是一个介于0和1之间的概率。模型的形式是一个S形的逻辑函数(sigmoid函数),但是sigmoid函数的参数到底要选哪个,就需要对sigmoid函数的结果进行评判,因此也就需要第二步:损失评估。
举个例子:
假设我们有一个逻辑回归模型,用来预测学生是否会通过最终考试。我们有两个特征:学生的出勤率和平均成绩。模型的目标是基于这些特征预测学生是否会通过考试("通过"记为1,"不通过"记为0)。
特征和参数
- 假设特征向量 x = [ x 1 x 2 ] x = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} x=[x1x2],其中 x 1 x_1 x1是学生的出勤率, x 2 x_2 x2是学生的平均成绩。
- 模型的参数为 θ = [ θ 0 θ 1 θ 2 ] \theta = \begin{bmatrix} \theta_0 \\ \theta_1 \\ \theta_2 \end{bmatrix} θ= θ0θ1θ2 ,其中 θ 0 \theta_0 θ0是偏置项, θ 1 \theta_1 θ1和 θ 2 \theta_2 θ2分别是与出勤率和平均成绩相关的权重。
计算 h ( x ) h(x) h(x)
模型会计算 h ( x ) h(x) h(x),即给定特征时通过考试的预测概率。这是通过sigmoid函数来完成的:
h θ ( x ) = 1 1 + e − ( θ 0 + θ 1 x 1 + θ 2 x 2 ) h_\theta(x) = \frac{1}{1 + e^{-(\theta_0 + \theta_1 x_1 + \theta_2 x_2)}} hθ(x)=1+e−(θ0+θ1x1+θ2x2)1
假设对于一个特定学生,出勤率 x 1 = 0.85 x_1 = 0.85 x1=0.85(85%),平均成绩 x 2 = 75 x_2 = 75 x2=75,而模型参数为 θ 0 = − 4 \theta_0 = -4 θ0=−4, θ 1 = 10 \theta_1 = 10 θ1=10, θ 2 = 0.05 \theta_2 = 0.05 θ2=0.05。那么 h ( x ) h(x) h(x)的计算为:
h θ ( x ) = 1 1 + e − ( − 4 + 10 × 0.85 + 0.05 × 75 ) h_\theta(x) = \frac{1}{1 + e^{-(-4 + 10 \times 0.85 + 0.05 \times 75)}} hθ(x)=1+e−(−4+10×0.85+0.05×75)1
计算这个表达式的值(这需要一些数学运算),假设结果是 h θ ( x ) ≈ 0.76 h_\theta(x) \approx 0.76 hθ(x)≈0.76。这意味着根据我们的模型,这个学生通过考试的预测概率是 76%。基于这个预测,由于概率大于0.5,我们可以预测这个学生会通过考试。
到这一步为止, θ 0 = − 4 \theta_0 = -4 θ0=−4, θ 1 = 10 \theta_1 = 10 θ1=10, θ 2 = 0.05 \theta_2 = 0.05 θ2=0.05实际上是我们随机(或经验)取的一组参数数值,但其并不是最佳的,所以就需要有一个代价函数来判断整体的损失(正确率),再进行梯度下降(或其他优化算法)来迭代地调整这些参数,以获得最小化损失。
在逻辑回归中,由于目标结果只有0和1两种情况,因此去计算一组数据的损失的时候就需要区分成两个函数:
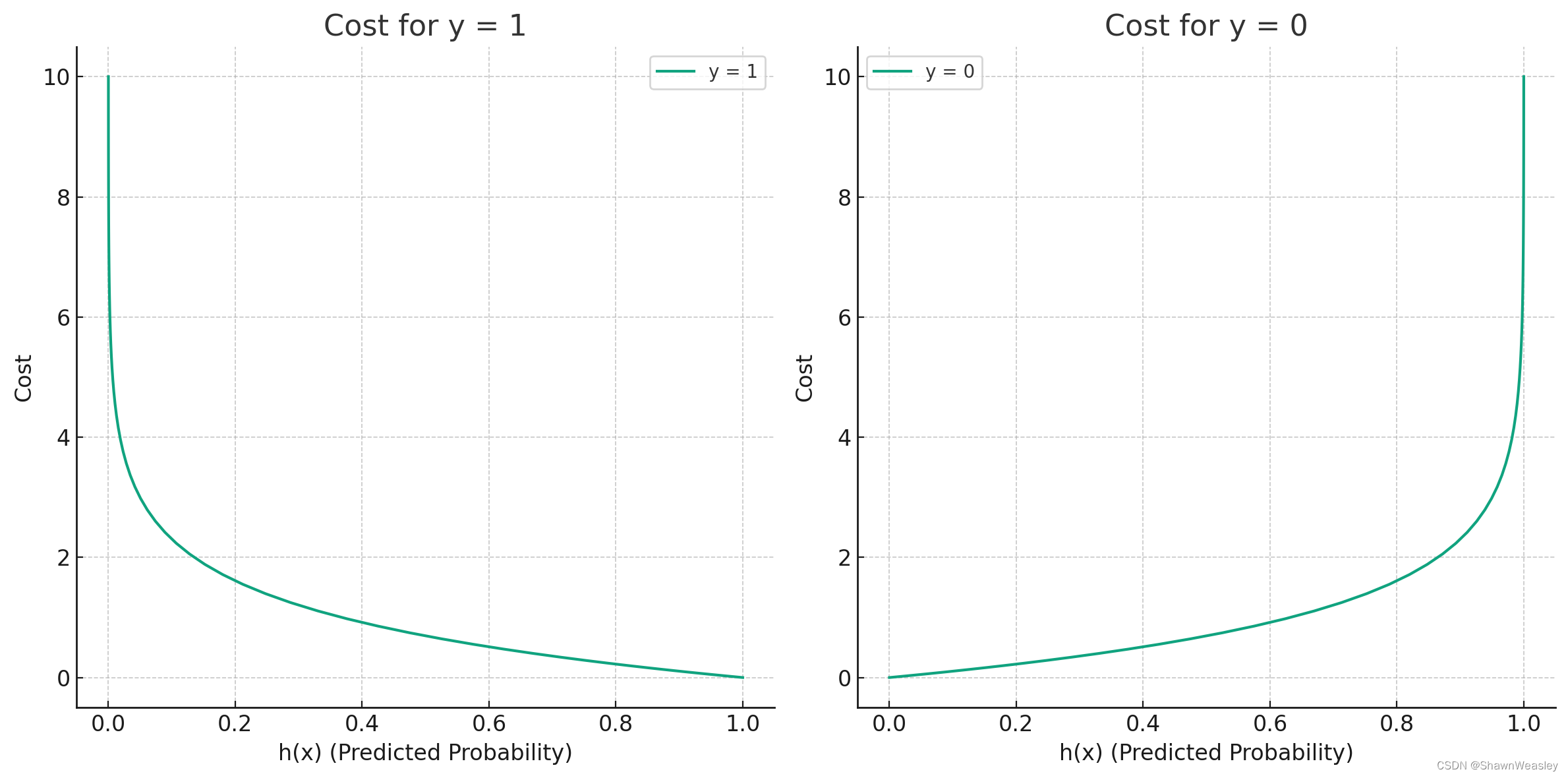
当 y=1 时的损失函数
Cost when y = 1 : − log ( h θ ( x ) ) \text{Cost when } y = 1: -\log(h_\theta(x)) Cost when y=1:−log(hθ(x))
当 y=0 时的损失函数
Cost when
y
=
0
:
−
log
(
1
−
h
θ
(
x
)
)
\text{Cost when } y = 0: -\log(1 - h_\theta(x))
Cost when y=0:−log(1−hθ(x))
对应的图如下:
用一个式子来同时包含这两个情况就是我们的逻辑回归的代价函数(交叉熵损失):
J
(
θ
)
=
−
1
m
∑
i
=
1
m
[
y
(
i
)
log
(
h
θ
(
x
(
i
)
)
)
+
(
1
−
y
(
i
)
)
log
(
1
−
h
θ
(
x
(
i
)
)
)
]
J(\theta) = -\frac{1}{m} \sum_{i=1}^{m} \left[ y^{(i)} \log(h_\theta(x^{(i)})) + (1 - y^{(i)}) \log(1 - h_\theta(x^{(i)})) \right]
J(θ)=−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]
我们可以看到这里
l
o
g
(
h
θ
(
x
(
i
)
)
)
log(h_\theta(x^{(i)}))
log(hθ(x(i)))前面乘以了
y
(
i
)
y^{(i)}
y(i),所以当目标值为0的时候,这部分就变成了0,也就不会影响后面部分的计算,就很简单地实现了两个式子融合。






















 9064
9064











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








