1. 基本介绍
同K均值类似,FCM算法也是一种基于划分的聚类算法,它的思想就是使得被划分到同一簇的对象之间相似度最大,而不同簇之间的相似度最小。
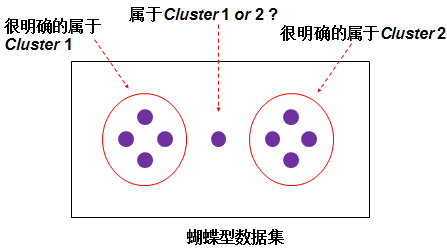
模糊C均值是普通C均值聚类算法的改进,普通C均值对数据进行硬性划分,一个样本一定明确的属于某一类,FCM对数据进行模糊划分,使用隶属度表示一个样本属于某一类的程度。实际聚类中可能会遇到这样的情况,蝴蝶形数据集中样本点的类别不好硬性判断,所以引入隶属度来进行模糊划分。
隶属度函数是表示一个对象x隶属于集合A的程度的函数,通常记做μA(x),其自变量范围是所有可能属于集合A的对象(即集合A所在空间中的所有点),取值范围是[0,1],即0<=1,μA(x)<=1。μA(x)=1表示x完全隶属于集合A,相当于传统集合概念上的x∈A。一个定义在空间X={x}上的隶属度函数就定义了一个模糊集合A,或者叫定义在论域X={x}上的模糊子集 。对于有限个对象x1,x2,……,xn模糊集合可以表示为:
2. 参数更新公式推导
a.隶属度矩阵:Uc×n
Uij 是第i 个样本属于第j个聚类的隶属度。
3. 步骤
(a)确定类别数C,参数m,和迭代停止误差Epslion以及最大迭代次数MaxIterationTimes
(b)初始化聚类中心P
(c)计算初始的距离矩阵D
(d)按下列公式更新隶属度:
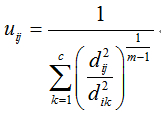
注意,如果有距离为0的情况出现,则把该点与相应类的隶属度设为1,其它设为0。
(e)更新聚类中心
(f)重新计算距离矩阵,并计算目标函数的值
(g)若达到最大迭代次数或者前后两次的J的绝对差小于迭代停止误差则停止,否则转(d),也可以使用前后两次隶属度矩阵的差来判断。
(h)将样本点划分为隶属度最大的那一类。
4. C实现(使用了opencv做数据显示)
#include "highgui.h"
#include <math.h>
#include <time.h>
#include "cv.h"
//FCM聚类,得到的结果从0开始计数
void myFCMeans(float* pSamples,int* pClusterResult,int clusterNum,int sampleNum,int featureNum,int m_Value);
void main()
{
#define MAX_CLUSTERS 5
CvScalar color_tab[MAX_CLUSTERS];
IplImage* img = cvCreateImage( cvSize( 500, 500 ), IPL_DEPTH_8U, 3 );
CvRNG rng = cvRNG(cvGetTickCount());
CvPoint ipt;
color_tab[0] = CV_RGB(255,0,0);
color_tab[1] = CV_RGB(0,255,0);
color_tab[2] = CV_RGB(100,100,255);
color_tab[3] = CV_RGB(255,0,255);
color_tab[4] = CV_RGB(255,255,0);
int i,k;
int clusterNum = cvRandInt(&rng)%MAX_CLUSTERS + 2; //至少有两类
int sampleNum = cvRandInt(&rng)%1000 + 100; //至少100个点
int feaNum=2;
CvMat* sampleMat = cvCreateMat( sampleNum, 1, CV_32FC2 );
/* generate random sample from multigaussian distribution */
//产生高斯随机数
for( k = 0; k < clusterNum; k++ )
{
CvPoint center;
int topIndex=k*sampleNum/clusterNum;
int bottomIndex=(k == clusterNum - 1 ? sampleNum : (k+1)*sampleNum/clusterNum);
CvMat* localMat=cvCreateMatHeader(bottomIndex-topIndex,1,CV_32FC2);
center.x = cvRandInt(&rng)%img->width;
center.y = cvRandInt(&rng)%img->height;
cvGetRows( sampleMat, localMat, topIndex,bottomIndex, 1 ); //此函数不会给localMat分配空间,不包含bottomIndex
cvRandArr( &rng, localMat, CV_RAND_NORMAL,
cvScalar(center.x,center.y,0,0),
cvScalar(img->width*0.1,img->height*0.1,0,0));
}
// shuffle samples 混乱数据
for( i = 0; i < sampleNum/2; i++ )
{
CvPoint2D32f* pt1 = (CvPoint2D32f*)sampleMat->data.fl + cvRandInt(&rng)%sampleNum;
CvPoint2D32f* pt2 = (CvPoint2D32f*)sampleMat->data.fl + cvRandInt(&rng)%sampleNum;
CvPoint2D32f temp;
CV_SWAP( *pt1, *pt2, temp );
}
float* pSamples=new float[sampleNum*feaNum];
int* pClusters=new int[sampleNum];
for (i=0;i<sampleNum;i++)
{
//feaNum=2
pSamples[i*feaNum]=(cvGet2D(sampleMat,i,0)).val[0];
pSamples[i*feaNum+1]=(cvGet2D(sampleMat,i,0)).val[1];
}
cvReleaseMat( &sampleMat );
cvZero( img );
for( i = 0; i < sampleNum; i++ )
{
//feaNum=2
ipt.x = (int)(pSamples[i*feaNum]);
ipt.y = (int)(pSamples[i*feaNum+1]);
cvCircle( img, ipt, 1, cvScalar(255,255,255), CV_FILLED, CV_AA, 0 );
}
cvSaveImage("origin.jpg",img);
myFCMeans(pSamples,pClusters,clusterNum,sampleNum,feaNum,2);
cvZero( img );
for( i = 0; i < sampleNum; i++ )
{
//feaNum=2
int cluster_idx = pClusters[i];
ipt.x = (int)(pSamples[i*feaNum]);
ipt.y = (int)(pSamples[i*feaNum+1]);
cvCircle( img, ipt, 1, color_tab[cluster_idx], CV_FILLED, CV_AA, 0 );
}
delete[] pClusters;
pClusters=NULL;
delete[] pSamples;
pSamples=NULL;
cvNamedWindow( "clusters");
cvShowImage( "clusters", img );
cvWaitKey(0);
cvDestroyWindow( "clusters" );
cvSaveImage("clusters.jpg",img);
cvReleaseImage(&img);
}
//FCM聚类,得到的结果从0开始计数
void myFCMeans(float* pSamples,int* pClusterResult,int clusterNum,int sampleNum,int featureNum,int m_Value)
{
if (m_Value<=1 || clusterNum>sampleNum)
{
return;
}
int i,j,k;
int int_temp;
float* pUArr=NULL; //隶属度矩阵
double* pDistances=NULL; //距离矩阵
float* pCenters=NULL; //聚类中心
int m=m_Value; //参数
int Iterationtimes; //迭代次数
int MaxIterationTimes=100; //最大迭代次数
double Epslion=0.001; //聚类停止误差
double VarSum; //平方误差和
double LastVarSum; //上一次的平方误差和
//申请空间以及初始化
pUArr=new float[sampleNum*clusterNum];
pDistances=new double[sampleNum*clusterNum];
pCenters=new float[clusterNum*featureNum];
//初始化中心点
srand((unsigned int)time(NULL));
int_temp=rand()%sampleNum;
for (i=0;i<clusterNum;i++)
{
for (j=0;j<featureNum;j++)
{
pCenters[i*featureNum+j]=pSamples[int_temp*featureNum+j];
}
int_temp+=(sampleNum/clusterNum);
if (int_temp>=sampleNum)
{
int_temp%=sampleNum;
}
}
//计算初始距离矩阵
for (i=0;i<sampleNum;i++)
{
for (k=0;k<clusterNum;k++)
{
double distance_temp=0;
for (j=0;j<featureNum;j++)
{
distance_temp+=(double)((double)(pCenters[k*featureNum+j]-pSamples[i*featureNum+j])*(pCenters[k*featureNum+j]-pSamples[i*featureNum+j]));
}
pDistances[i*clusterNum+k]=distance_temp;
}
}
//开始聚类
Iterationtimes=0;
LastVarSum=0;
VarSum=0;
while(1)
{
Iterationtimes++;
//更新隶属度矩阵
//计算隶属度,聚类矩阵已更新
for (i=0;i<sampleNum;i++)
{
double denominator=0; //(1/Dik^2)^(1/(m-1))
bool isEqualCenter=false; //是否有距离为0的情况
int category_temp; //如果有距离为0的情况所判别的类
for (k=0;k<clusterNum;k++)
{
double currentDis=pDistances[i*clusterNum+k];
if (currentDis!=0)
{
denominator+=pow(1.0/pDistances[i*clusterNum+k],1.0/(m-1));
}
else
{
isEqualCenter=true;
category_temp=k;
break;
}
}
//如果有距离为0的情况,就把相应类的隶属度置为1,其它为0
if (true==isEqualCenter)
{
for(k=0;k<clusterNum;k++)
{
pUArr[i*clusterNum+k]=0;
}
pUArr[i*clusterNum+clusterNum]=1.0;
}
else
{
for (k=0;k<clusterNum;k++)
{
pUArr[i*clusterNum+k]=pow(1.0/pDistances[i*clusterNum+k],1.0/(m-1))/denominator;
}
}
}
//更新聚类中心
for (k=0;k<clusterNum;k++)
{
double denominator=0;
for (j=0;j<featureNum;j++)
{
double numerator=0;
for (i=0;i<sampleNum;i++)
{
double U_m_temp=pow(pUArr[i*clusterNum+k],m_Value);
if (0==j)
{
denominator+=U_m_temp;
}
numerator+=(U_m_temp*pSamples[i*featureNum+j]);
}
pCenters[k*featureNum+j]=numerator/denominator;
}
}
//计算平方误差函数值,并更新距离矩阵
VarSum=0;
for (i=0;i<sampleNum;i++)
{
for (k=0;k<clusterNum;k++)
{
double distance_temp=0;
for (j=0;j<featureNum;j++)
{
distance_temp+=(double)((double)(pCenters[k*featureNum+j]-pSamples[i*featureNum+j])
*(pCenters[k*featureNum+j]-pSamples[i*featureNum+j]));
}
pDistances[i*clusterNum+k]=distance_temp;
VarSum+=(pow(pUArr[i*clusterNum+k],1.0/m)*distance_temp); //存在溢出危险
}
}
if (Iterationtimes>=MaxIterationTimes || fabsl(VarSum-LastVarSum)<=Epslion)
{
break;
}
LastVarSum=VarSum;
}
delete[] pDistances;
pDistances=NULL;
delete[] pCenters;
pCenters=NULL;
//分类,归为隶属度最大的那一类
for (i=0;i<sampleNum;i++)
{
float maxU; //最大隶属度
int Category; //属于类别
for (k=0;k<clusterNum;k++)
{
if (0==k || maxU<pUArr[i*clusterNum+k])
{
Category=k;
maxU=pUArr[i*clusterNum+k];
}
}
pClusterResult[i]=Category;
}
delete[] pUArr;
pUArr=NULL;
}5. 结果













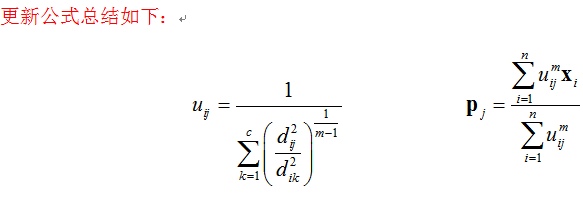
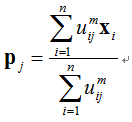
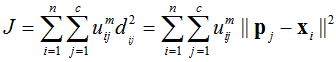














 6772
6772

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








