LoRA: Low-Rank Adaptation of Large Language Models低秩自适应

DeepBERT

已于 2023-11-13 18:07:07 修改

阅读量4.5k

点赞数 2

分类专栏： NLP 文章标签： nlp

于 2023-02-23 16:45:42 首次发布

本文链接：https://blog.csdn.net/emphmeral/article/details/129184347

版权

NLP 专栏收录该内容

3 篇文章 1 订阅

订阅专栏

低秩自适应（LoRA），它将预训练模型权重冻结，并将可训练的秩分解矩阵注入Transformer架构的每一层，大大减少了下游任务的可训练参数数量。具体来说，它将原始矩阵分解为两个矩阵的乘积，其中一个矩阵的秩比另一个矩阵的秩低。这时只需要运用低秩矩阵来进行运算，这样，可以减少模型参数数量，提高训练吞吐量，并且在模型质量上表现出色，且不会增加推理延迟。

LoRA的思想也很简单，在原始PLM旁边增加一个旁路，做一个降维再升维的操作，来模拟所谓的intrinsic rank。训练的时候固定PLM的参数，只训练降维矩阵A与升维矩阵B。而模型的输入输出维度不变，输出时将BA与PLM的参数叠加。用随机高斯分布初始化A，用0矩阵初始化B，保证训练的开始此旁路矩阵依然是0矩阵。

这种思想有点类似于残差连接，同时使用这个旁路的更新来模拟full finetuning的过程。并且，full finetuning可以被看做是LoRA的特例（当r等于k时）：

This means that when applying LoRA to all weight matrices and training all biases, we roughly recover the expressiveness of full fine-tuning by setting the LoRA rank r to the rank of the pre-trained weight matrices.
In other words, as we increase the number of trainable parameters, training LoRA roughly converges to training the original model, while adapter-based methods converges to an MLP and prefix-based methods to a model that cannot take long input sequences.

LoRA也几乎未引入额外的inference latency，只需要计算 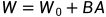$\text{[math]}$ 即可。

LoRA与Transformer的结合也很简单，仅在QKV attention的计算中增加一个旁路，而不动MLP模块：

We limit our study to only adapting the attention weights for downstream tasks and freeze the MLP modules (so they are not trained in downstream tasks) both for simplicity and parameter-efficiency.

为了获得更好的直觉，想象你有一个权重矩阵 W ，它的维度为 768 x 768 。现在我们可以将矩阵分解为两个矩阵 W_A 和 W_B ，使得 W_A (768 x r) 和 W_B (r x 768) 。现在我们可以将我们的矩阵W定义为 W = W_A @ W_B （其中 @ 是矩阵乘法）。因此，最初 W 的可训练参数的数量是768 * 768 = 589824，而现在作为 W_A 和 W_B 的分解的W的可训练参数的总数变为768 × 8）+（8 × 768）= 12288，这是参数减少了97%。这里有一个伪代码来更好的理解这一点

import torch 
import torch.nn as nn

# 定义神经网络的输入和输出维度
# 定义权重矩阵的大小
# 让假设权重矩阵的大小变成维度的W(768 X 768)
# W中的参数总数为768*768=589824

input_dim = 768 
output_dim = 768 
W = ... # weight of my neural network

# 等级‘r’用于低等级适配
# 可以将权重W表示为两个矩阵W_A和W_B的乘积，使得
# W(768 X 768)=W_A(768 X R)@(R X 768)
# 现在的参数总数是(768×8)+(8×768)=12288
# 因此我们将W_A和W_B定义为r=8

rank = 8 
W_A = nn.Parameter(torch.empty(input_dim, rank)) # LoRA weight A
W_B = nn.Parameter(torch.empty(rank, output_dim)) # LoRA weight B

# 加权为W的常规前向神经网络模型

def regular_forward_matmul(x, W):
    h = x @ W
    return h

# LoRA前向神经网络

def lora_forward_matmul(x, W, W_A, W_B):
    # 常规矩阵乘法 
    # where W is NOT trainable (froozen weights)
    h = x @ W  
    h += x @ (W_A @ W_B) * alpha    # use scaled LoRA weights
    return h

Hugging Face的PEFT库可以对LoRA进行调用，代码如下：


from peft import get_peft_model, LoraConfig, TaskType

peft_config = LoraConfig(
    task_type=TaskType.CAUSAL_LM, # 设置任务类型
    inference_mode=False,  # 设置推理模式为 False
    r=8,  # 设置 PEFT 模型的秩为 8
    lora_alpha=32, # 设置 LORA 的 alpha 参数为 32
    lora_dropout=0.1, # 设置 LORA 的 dropout 参数为 0.1
    target_modules=['query_key_value']  # 设置 PEFT 模型的目标模块为 ['query_key_value']
)

# 加载模型
model = AutoModelForSeq2SeqLM.from_pretrained(model_name_or_path)
model = get_peft_model(model, peft_config)

# 打印模型参数
model.print_trainable_parameters()
# output: trainable params: 2359296 || all params: 1231940608 || trainable%: 0.19151053100118282

# 然后就可以愉快地使用模型来训练了