Dijkstra的讲解与应用

简介

• Dijkstra 算法常用于求无负权边图中的最短路，在优化后有比 Bellman-Ford 算法优秀很多的时间复杂度，实际做题过程中有着更多的应用。

Dijkstra

简介

• 再进行具体讲解之前，我们先定义以下记号:
  • G = <V, E> 代表我们要处理的简单有向图；
  • n = |V|, m = |E| 代表定点数和边数；
  • l(u, v) 代表 u 到 v 的边的长度（边权）；
  • S 代表起点，E代表终点（如果有的话）
  • dist(u) 代表我们当前求出的从S到u的最短路径的长度，后面称为u的距离；

操作

• 我们要维护一个顶点集合 C，满足对于所有集合 C 中的顶点 x,我们都已经找到了起点 S到x的最短路，此时 dist(x)记录的就是最终最短路的长度。
• Dijkstra 算法流程如下：
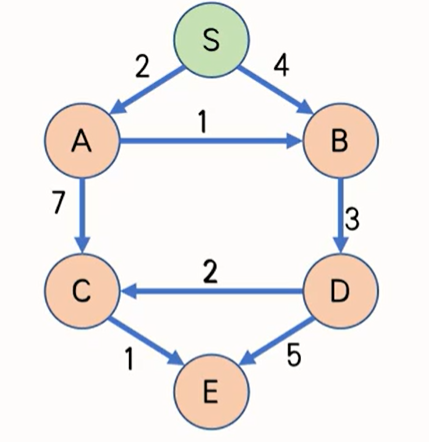
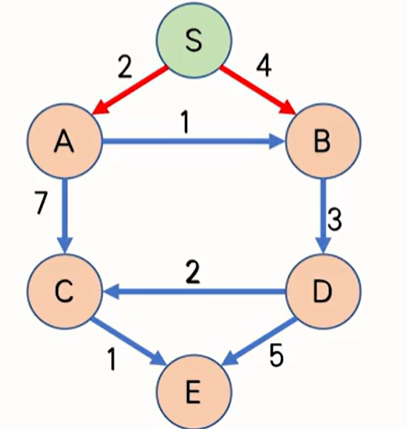
  • 将 C 设置为空，将S的距离设置为 0，其余点的距离设置为无穷大；
  • 在每一轮中，将离起点最近的(dist最小，不能是无穷大)的还不在C中的顶点加入C，并且用这个点连出去的边通过松弛操作尝试更新其它点的 dist;
  • 当 T(如果 T 存在的话)或者没有新的点加入 C 时，算法结束。
• 由于图上不存在负权边，可以证明每次加入 C 的点都已经找到了从起点到它的最短路。

具体实施

• 对此图进行Dijkstra;
  
• 初始时将 C 设置为空，将S的距离设置为 0，其余点的距离设置为无穷大。
• 在每一轮中，将离起点最近的(dist最小，不能是无穷大)的还不在C中的顶点加入C，并且用这个点连出去的边通过松弛操作尝试更新其它点的 dist。

顶点编号	距离
S	0
A	∞
B	∞
C	∞
D	∞
E	∞

• 迭代结果
  

顶点编号	距离	原因
S	0	0
A	2	l(S, A)
B	3	dist© + l(C, B)
C	8	dist(A) + l(A, C)
D	6	dist(E) + l(E, D)
E	9	l(S, E)

代码实现

• 将 C 设置为空，将S的距离设置为 0，其余点的距离设置为无穷大；
• 在每一轮中，将离起点最近的(dist最小，不能是无穷大)的还不在C中的顶点加入C，并且用这个点连出去的边通过松弛操作尝试更新其它点的 dist;
• 当 T(如果 T 存在的话)或者没有新的点加入 C 时，算法结束。
• 时间复杂度 O(n²+m)。

struct Node {
    int y, v;
    Node(int _y, int _v) { y = _y; v = _v;}; // 构造函数
};

vector<Node> edges[1001];
int n, m, dist[1001];
bool b[1001];

inline int Dijkstra(int s, int e) {
    memset(b, false, sizeof(b));
    memset(dist, 127, sizeof(dist));
    dist[s] = 0;
    while (true) {
        int x = -1;
        for (int i = 1; i <= n; i++)
            if (!b[i] && dist[i] < 1 << 30)
                if (x == -1 || dist[i] < dist[x])
                    x = i;
        if (x == e || x == -1)
            break;
        b[x] = true;
        for (auto i : edges[x])
            dist[i.y] = min(dist[i.y], dist[x] + i.v);
    }
    return dist[e];
}

算法演示

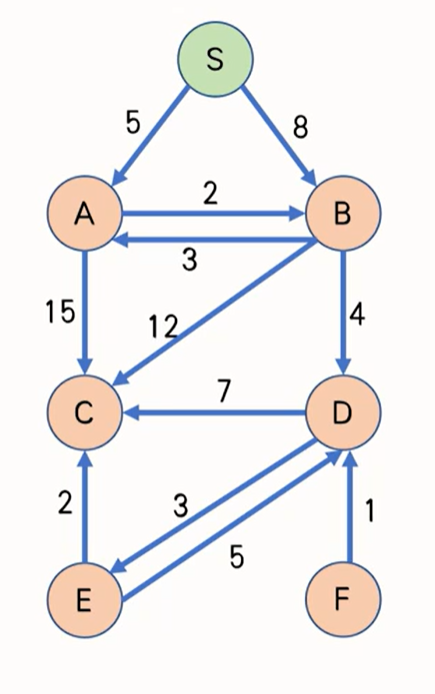
• 让我们在另一张图上在演示一遍 Dijkstra 算法。
  

当前节点	A	B	C	D	E	F
S	5	8	∞	∞	∞	∞
A	5	7	20	∞	∞	∞
B	5	7	19	11	∞	∞
C	5	7	18	11	14	∞
D	5	7	16	11	14	∞
E	5	7	16	11	14	∞
F

算法优化

• 观察前面的代码，发现我们花费了大量时间在找出 dist 的最小值上。
• 我们可以采用一个堆（优先队列）来维护 dist 数组，算法时间复杂度可以提升至 O((n+m)log n)。
• 在这里我们使用 set。

struct Node {
    int y, v;
    Node(int _y, int _v) { y = _y; v = _v;};
};

set< pair<int, int> > q; // 记录所有还不在集合C里面的点的信息（dist和下标）
vector<Node> edges[1001];
int n, m, dist[1001];

int Dijkstra(int s, int e) {
    memset(dist, 127, sizeof(dist));
    dist[s] = 0; q.clear();
    for (int i = 1; i <= n; i++)
        q.insert(make_pair(dist[i], i));
    for (; !q.empty();) {
        int x = q.begin()->second;
        q.erase(q.begin());
        if (x == e || dist[x] > 1 << 30)
            break;
        for (auto i : edges[x])
            if (dist[x] + i.v < dist[i.y]) { // 对q里面的i.y更新
                q.erase(make_pair(dist[i.y], i.y)); // 删除原本
                dist[i.y] = dist[x] + i.v; // 更新i.y
                q.erase(make_pair(dist[i.y], i.y)); // 插入现在
            }
    }
    return dist[e];
}