7.4.3 最小生成树

问题的引入（构造最小代价生成树）

• 假设要在 n 个城市之间建立通信联络网，则连通 n 个城市只需要 n-1 条线路。此时需要考虑如何在最节省经费的前提下建立这个通信网。
  在每两个城市之间都可以设置一条线路，相应的都要付出一定的经济代价， n 个城市之间最多可以设置 n( n-1 ) / 2 条线路（无向图），需要在其中选择 n-1 条，使得总的耗费最少。

• 使用 连通网 来表示 n 个城市以及 n 个城市间可能设置的通信线路，其中 网的顶点 表示城市，边 表示两城市之间的线路，每条边的权值 表示相应的代价。

• 对于 n 个顶点的连通网 可以建立许多不同的生成树，每一棵生成树 都可以是 一个通信网。
  现在要选择一棵生成树，使得总的耗费最少。
  这就是如何构造连通网的最小代价生成树的问题。
  一棵生成树的代价 就是 树上各边代价之和。

MST性质

• 假设 N = ( V , { E } ) 是一个连通网，U 是 顶点集V 的一个 非空子集。若 ( u , v ) 是一条 具有最小权值 ( 代价 ) 的边，其中 u ∈ U，v ∈ V - U，则必存在一棵包含 边 ( u , v ) 的最小生成树。

• 使用 反证法 证明上面的性质：
  假设网 N 的 任意一棵最小生成树 都不包含 ( u , v )。
  设 T 是连通网上的一棵最小生成树，当将边 ( u , v ) 加入到 T 中，由于生成树的定义，T 中必存在一条包含 (u , v) 的回路。
  另一方面，由于 T 是生成树，则在 T 上必存在另一条边 ( u’ , v’ )，其中 u’ ∈ U，v’ ∈ V - U，且 u 和 u’ 之间有路径相通，v 和 v’ 之间均有路径相通。删去边（u’ , v’），便可消除上述回路，同时得到另一棵生成树 T’ 。
  因为（u , v）的代价不高于（u’ , v’）的代价，则 T’ 的代价亦不高于 T，T’ 是 包含（u , v）的一棵最小生成树。由此和假设矛盾。
  【注意，（u’ , v’） 就是跨过 集合U 和 集合V-U 分界线的那条线】

• 基于MST性质的构造最小生成树的两个算法
  1、Prim算法
  2、Kruskal算法

Prim算法

• 假设 N = ( V , {E} ) 是连通网，TE 是 N 上最小生成树中边的集合。
  Prim算法
  从 U = { U₀ } （u₀ ∈ V），TE = { } 开始，重复执行下述操作：
  在所有 u∈U，v∈V - U 的边（u , v）∈ E 中找到一条代价最小的边 （u₀ , v₀）并入集合 TE，同时 v₀ 并入 U，直到 U=V 为止。
  此时 TE 中必有 n-1 条边，则 T = ( V , {TE} ) 为 N 的最小生成树。

• 为实现这个算法需附设一个 辅助数组 closedge，以记录从 U 到 V-U 具有最小代价的边。
  对每个顶点 v_i ∈ V-U，在辅助数组中存在一个相应分量 closedge [ i-1 ]，它包括 2 个域，
  其中 lowcost域存储该边上的权。vex域 存储该边依附的在 U 中的顶点。
  closedge [ i - 1] . lowcost = Min { cost ( u, v_i ) | u ∈ U }
  生成过程图示如下：
  
  
  例如，上图为按 Prim算法 构造 网的一棵最小生成树 的过程，在构造过程中辅助数组中各分量值的变化如上图所示
  由于 U = { V₁ }，则 到 V - U 中各顶点的最小边，即为从 依附于 顶点1 的各条边中，找到一条代价最小的边（u₀ , v₀）= （1 , 3）为生成树上的第一条边，同时将 v₀（= v₃）并入 集合U。
  然后修改辅助数组的值，首先将 closedge [ 2 ] . lowcost 改为 ‘0’，以示顶点 v₃ 已并入 U。
  然后，由于 边（v₃ , v₂）的权值小于 closedge[ 1 ] . lowcost，则需修改 closedge[ 1 ] 为 边（v₃ , v₂）及其权值。
  同理，修改 closedge[ 4 ] 和 closedge[ 5 ]，依此类推，直到 U = V。

• Prim算法代码
  以 二维数组 表示网的邻接矩阵，且设两个顶点之间不存在的边的权值 为 机内允许的最大值（INT_MAX）

// 利用 prim算法 从 网G 第 u 个顶点出发，构造
// 网G 的最小生成树
void MiniSpanTree_Prim(MGraph G, VertexType u)
{
 	// 设辅助数组记录代价最小的边
	struct
	{
		VertexType adjvex; //边所依附的顶点，另一个closedge的数组号
		VRType lowcost; //边的权值 
	} closedge[MAX_VERTEX_NUM];
	k = LocateVex(G, u); // u 作为起始点
	for(j=0; j<G.vexnum; j++) // 辅助数组初始化
	{
		if(j != k)
		{
			closedge[j] = {u, G.arcs[k][j].adj};
		}
	}
	closedge[k].lowcost = 0; // 第k个顶点并入u集
	for(i=1; i<G.vexnum; i++)
	{
		k = minimum(closedge);
		printf(closedge[k].adjvex, G.vexs[k]);// 输出生成树的边
		closedge[k].lowcost = 0; // 第k个顶点并入u集
		for(j=0; j<G.vexnum; j++)
		{
		  	// 新顶点并入 U 后重新选择最小边
			if(G.arcs[k][j].adj < closedge[j].lowcost)
			{
				closedge[j] = {G.vexs[k], G.arcs[k][j].adj};
			}
		}
	}
}

• Krim算法的 时间复杂度 为 O(n²)
  算法中第一个初始化的循环语句的频度是 n。
  第二个循环语句的频度是 n-1 。其中有两个内循环，其一是在 closedge[ v ] . lowest 中求最小值，其频度为 n - 1。其二是重新选择具有最小代价的边，频度为 n。
  时间复杂度与网中的边数无关，适用于求边稠密的网的最小生成树。

Kruskal算法

• 假设连通网 N =（V , {E}），则令最小生成树的 初始状态 为只有 n 个顶点而无边的非连通图 T =（ V , { } ），图中每个顶点自成一个连通分量。
  在 E 中选择一个 代价最小的边，若该边依附的顶点 落在 T 中不同的连通分量上，则将此边加入到 T 中，否则会舍去此边而选择下一条代价最小的边。
• 关系集 E
  
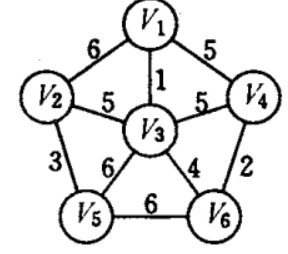
• Kruskal算法构造最小生成树的过程
  
  代价分别为 1，2 ，3，4 的 4 条边由于满足了上述条件，则先后被加入到 T 中。
  代价为 5 的两条边（v₁ , v₄）和（v₃ , v₄）被舍去，因为它们依附的两顶点在同一连通分量上，它们若加入 T 中，则会使 T 中产生回路，
  而下一条代价（ 5 ）最小的边（v₂ , v₃）联结两个普通分量，则（v₂ , v₃）可以加入 T。
  由此构造成一棵最小生成树。
  
• 时间复杂度
  上述算法最多对 e 条边各扫描一次，时间复杂度 为 O ( e * log e ) （e 为网中边的数目）。
  相比 Prim算法，Kruskal算法适合求边稀疏的网的最小生成树。
  上述算法至多对 e 条边各扫描一次，假若以第 9 章介绍的 “堆” 来存放网中的边，则每次选择最小代价的边仅需 O ( log e ) 的时间（第一次需 O ( e )）。